Difficult examples

1.  Simplify

`4/sqrt8` 

The first thing you should attempt is to rationalise the denominator.

`4/sqrt8=4/{sqrt8timessqrt8/sqrt8}=4/{{sqrt8timessqrt8}/sqrt8}=4/{{8}/sqrt8}`

So we have rationalised the denominator

i.e.

`4/sqrt8=4/(8/sqrt8)`

But we can go further

`4/{{8}/{sqrt8}}={4timessqrt8}/8=sqrt8/2`

But now we can also simplify square roots

Simplify  `sqrt8`

Write down what we know

`2=sqrt4,\ \ \ \  3=sqrt9,\ \ \ \  4=sqrt16`

`5=sqrt25,\ \  6=sqrt36,\ \  7=sqrt49`

`sqrt8=sqrt(4times2)`

Try something we know using `sqrt9`

`sqrt(9times4)=sqrt36=6` 

Is that the same as

`sqrt9timessqrt4=3times2=6` 

Yes it is

Therefore `sqrt(4times2)=sqrt4timessqrt2`

               `sqrt4timessqrt2=2timessqrt2`

To finish

`sqrt8/2=(cancel2timessqrt2)/cancel(2)=sqrt2`  

Answer:  `4/sqrt8=sqrt2`

 

2.  Simplify `sqrt(a^3)`

Try something we know using `sqrt9`

We know `sqrt(9^2)` is the same as

`sqrt9timessqrt9` 

i.e. both = 9 

Therefore  `sqrt(9^3)=sqrt9timessqrt9timessqrt9`

Is the same as

`=sqrt(9^2)timessqrt9=9sqrt9`

Therefore  `=sqrt(a^3)` 

Is the same as

`=sqrt(a^2)timessqrta=asqrta`

Answer:  `sqrt(a^3)=asqrta`

 

3.  Rationalise the denominator

`2/(9sqrt5)`

Rationalise the denominator = Turn the surd of the denominator into a fraction.

`2/{9sqrt5}=2/{{9timessqrt5timessqrt5}/sqrt5}=2/{{9times5}/sqrt5}=2/{45/sqrt5}` 

We have rationalised the denominator but we can go further

`2/{{45}/sqrt5}={2sqrt5}/45`

Answer:  `2/{9sqrt5}={2sqrt5}/45` 

 

4.  Simplify

 `(3+sqrt2)(3-sqrt2)` 

Multiply out

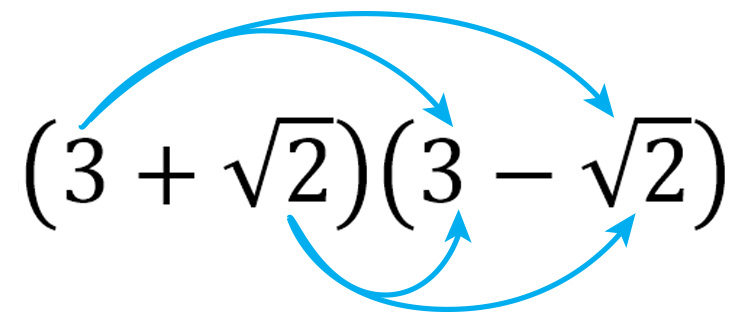
`=3times3+3times(-sqrt2)+3timessqrt2-sqrt2timessqrt2` 

`=9-3sqrt2+3sqrt2 -sqrt(2times2)` 

`=9-cancel(3sqrt2)+cancel(3sqrt2) -sqrt4`  

`=9-2`    

`= 7`     

Answer: = 7

 

5.  Simplify

`(x+sqrty)^2` 

Multiply out

 

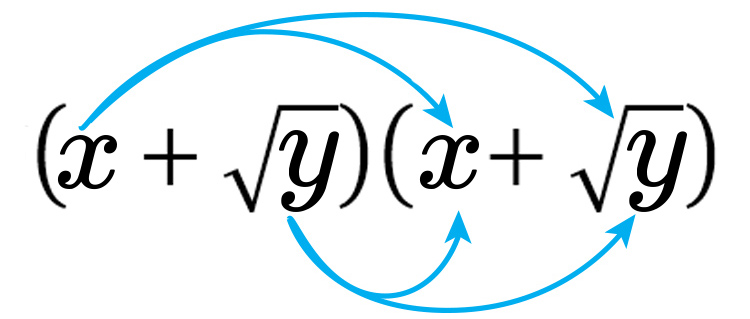
Answer:  

`=x^2+xsqrty+xsqrty+sqrtytimessqrty` 

`=x^2+2xsqrty+sqrtytimessqrty` 

`=x^2+2xsqrty+sqrt(y^2)` 

`=x^2+2xsqrty+y` 

Answer:  `=x^2+2xsqrty+y` 

 

6.  Simplify

 `(x+sqrty)(x-sqrty)` 

Multiply out

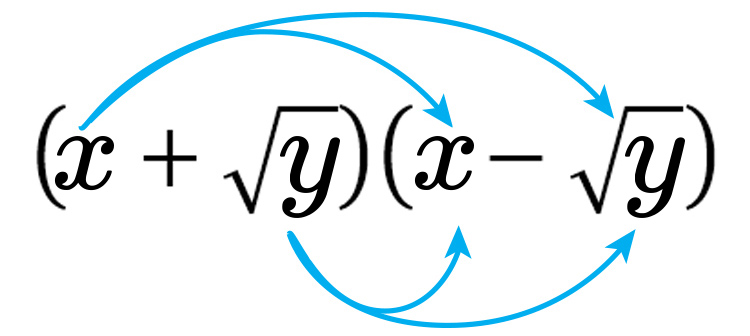
`=x^2-xsqrty+xsqrty-sqrtytimessqrty` 

`=x^2-cancel(xsqrty)+cancel(xsqrty)-sqrt(y^2)` 

`=x^2-y`

Answer: `=x^2-y` 

 

 7.  Simplify

`6sqrt2+sqrt18` 

First simplify

 `sqrt18` 

Write down what we know

`2=sqrt4,\ \ \ \  3=sqrt9,\ \ \ \  4=sqrt16`

`5=sqrt25,\ \  6=sqrt36,\ \  7=sqrt49`

The biggest square that divides into 18 is 9.

Therefore `sqrt18 = sqrt(2times9)` 

Try something we know using  `sqrt9` 

`sqrt(4times9)=sqrt36=6`

Is that the same as

`sqrt4timessqrt9=3times2=6`  

Yes it is

Therefore `sqrt(2times9)=sqrt2timessqrt9` 

               `sqrt2timessqrt9=3timessqrt2` 

So now getting back to the original question

       `6sqrt2+sqrt18` 

`=6sqrt2+3sqrt2` 

Try something we know using `sqrt9` 

`6sqrt9+3sqrt9=6times3+3times3`

`=18+9=27` 

Is that the same as 

`(6+3)sqrt9=9sqrt9=9times3=27` 

Yes it is

Therefore  `6sqrt2+3sqrt2` 

`=(6+3)sqrt2` 

`=9sqrt2`  

Answer:  `6sqrt2+sqrt18=9sqrt2`  

 

8.  Simplify

`8sqrt10times5sqrt15`   

`8timessqrt10times5timessqrt15`  

`8times5timessqrt10timessqrt15`  

 `40sqrt15timessqrt10` 

Try something we know using  `sqrt9`  

`sqrt9 timessqrt4=3times2=6`   

Is that the same as

`sqrt(9 times4)=sqrt36=6`   

Yes it is

Therefore `40sqrt15timessqrt10`  

`=40timessqrt(15times10)`   

`=40sqrt150`

So now simplify

`sqrt150`  

Write down what we know

`2=sqrt4,\ \ \ 3=sqrt9,\ \ \ \ \ \ 4=sqrt16`

`5=sqrt25,\ \  6=sqrt36,\ \ \ 7=sqrt49`

`8=sqrt64,\ \ 9=sqrt81,\ \ 10=sqrt100`

The biggest square that divides into 150 = 25.   

Therefore `sqrt150=sqrt(3times25)=sqrt3timessqrt25`

         `sqrt3timessqrt25=5sqrt3`              

Get back to

`40sqrt150`

This now equals

`40times5sqrt3`

Therefore `200sqrt3`

Answer:  `8sqrt10times5sqrt15=200sqrt3` 

 

9.  Simplify

 `(5sqrt6+4sqrt3)(3sqrt6-2sqrt3)` 

First multiply out the brackets

 

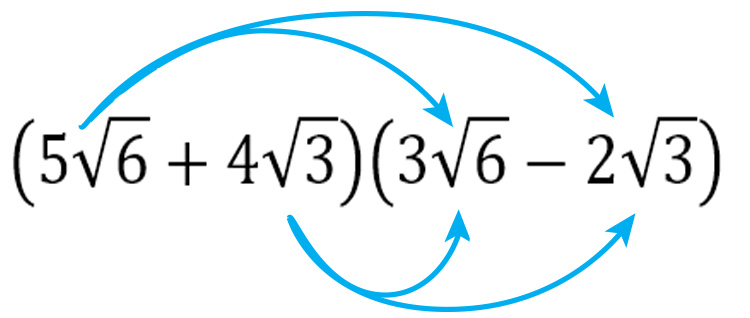
`5sqrt6times3sqrt6-2sqrt3times5sqrt6+4sqrt3times3sqrt6-2sqrt3times4sqrt3` 

Working on BIDMAS

Stage 1

Work out  `5sqrt6times3sqrt6` 

Try something we know using `sqrt9` 

`5sqrt9times3sqrt9=5times3times3times3`

`=15times9` 

Is that the same as

`5times3timessqrt(9times9)=5times3timessqrt81`

`=15times9`  

Yes it is

Therefore `5timessqrt6times3timessqrt6` 

 `=5times3timessqrt6timessqrt6` 

`=15sqrt36` 

`=15times6` 

`=90` 

Stage 2

Work out  `-2sqrt3times5sqrt6` 

Try something we know using  `sqrt9` 

`-2timessqrt9times5timessqrt4`

`=-2times3times5times2`

`=-6times10=-60` 

Is this the same as

`-2times5timessqrt(9times4)`

`=-10timessqrt36`

`=-10times6=-60`  

Yes it is

Therefore `-2timessqrt3times5timessqrt6` 

`=-2times5timessqrt3timessqrt6` 

`=-10timessqrt(3times6)` 

`=-10timessqrt18` 

But we can simplify

 `sqrt18` 

Write down what we know

 `2=sqrt4`,   `3=sqrt9`,   `4=sqrt16`

Therefore  `sqrt18=sqrt(9times2)=sqrt9timessqrt2`

`sqrt18=3timessqrt2`

Going back

Therfore `-10timessqrt18` 

 `-10times3timessqrt2`

`-30sqrt2`

Stage 3

 `4sqrt3times3sqrt6`

As stage 2

`4timessqrt3times3timessqrt6`

`4times3timessqrt3times sqrt6`

`12timessqrt3timessqrt6`

`12timessqrt(3times6`

`12timessqrt18`

We know from stage 2

 `sqrt18=3timessqrt2`

Therefore  `12timessqrt18=12times3timessqrt2=36sqrt2`

Stage 4

`-2sqrt3times4sqrt3`

As stage 2

 `-2timessqrt3times4timessqrt3`

`-2times4timessqrt3timessqrt3`

`-8timessqrt(3times3)`

`-8timessqrt9`

`-8times3`

`-24`

Putting all the stages together:

 `90-30sqrt2+36sqrt2-24`

`90+6sqrt2-24`

`90-24+6sqrt2`

`66+6sqrt2`

Answer:  `(5sqrt6+4sqrt3)(3sqrt6-2sqrt3)`

`=66+6sqrt2`