Ratios in the form `1:n` or `n:1`
In order that a ratio is written in the form `1:n` we must make the left hand side equal to one.
In order that a ratio is written in the form `n:1` we must make the right hand side equal to one.
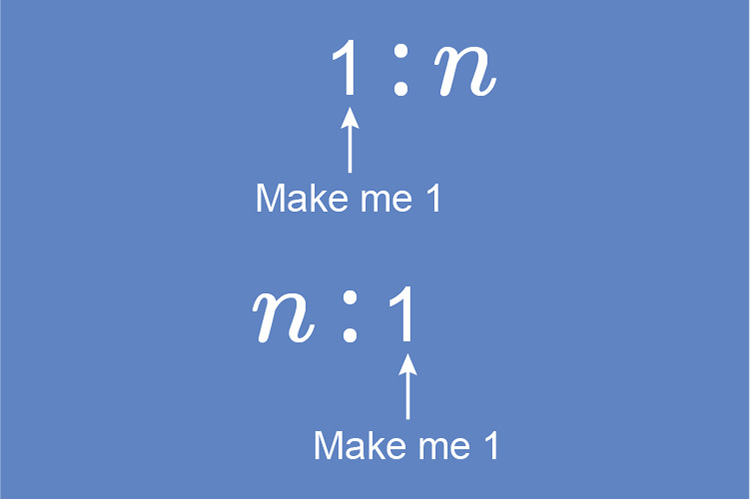
NOTE:
`n` can be expressed as a decimal or a fraction
Example 1
Express `6:10` in the form `1:n`
So the ratio is
`6:10`
and we need to work out
`1:n`
(see our section on percentages for full explanation)
`6:10`
`1:n`
Now put a divide sign in
`6/1=10/n`
Rearranging the formula
`n=(10times1)/6`
`n=10/6`
simplifying the fraction
`n=5/3`
So the ratio in the form `1:n` is
`1:5/3`
Example 2
Express `6:10` in the form `n:1`
So the ratio is
`6:10`
and we need to work out
`n:1`
(see our section on percentages for full explanation)
`6:10`
`n:1`
Now put a divide sign in
`6/n=10/1`
Rearranging the formula
`(6times1)/10=n` or
`n=(6times1)/10`
`n=6/10`
simplifying the fraction
`n=3/5`
So the ratio in the form `n:1` is
`3/5:1`
Example 3
The ratio of girls to boys in a school is:
`800` boys to `1200` girls
What is the ratio in the form `n:1`?
So the ratio is
`800:1200`
and we need to work out
`n:1`
(see our section on percentages for full explanation)
`800:1200`
`n:1`
Now put a divide sign in
`800/n=1200/1`
Rearranging the formula
`(800times1)/1200=n` or
`n=(800times1)/1200`
`n=800/1200`
simplifying the fraction
`n=(8cancel00)/(12cancel00)`
`n=8/12`
simplify the fraction further
`n=4/6`
simplify the fraction further
`n=2/3`
This will not simplify any further so the answer is
`2/3:1`
Example 4
A chief is cooking a meal for many and she knows that she has to buy `3` carrots to `8` parsnips. She also knows that the ratio of parsnips to broccoli is `6` parsnips to `1` broccoli. Write out the ratio in the form `A:B:C`
The ratio is `3` carrots `:8` parsnips and
`6` parsnips `:1` broccoli
Line these up we would have
`3` carrots `:8` parsnips and `6` parsnips `:1` broccoli
We need to make the second ratio have 8 parsnips i.e. the same as the first ratio.
Therefore
`6` parsnips `:1`
and we need to work out
`8` parsnips `:n`
(see our section on percentages for full explanation)
`6:1`
`8:n`
Now put a divide sign in
`6/8=1/n`
rearranging the formula
`n=(1times8)/6`
`n=8/6`
Simplify the fraction
`n=4/3`
So the new ratio is
`8` parsnips `:4/3` broccoli
So the full ratio is
`3` carrots `:8` parsnips and `8` parsnips `:4/3` broccoli
Which is the same as
`3` carrots `:8` parsnips `:4/3` broccoli




