Graphs - Always make `y` the subject of the formula
The formula for a straight line is `y=mx+c`
If you are given the formula:
`3y-2x=8`
Always make `y` the subject of the formula.

To make `y` the subject of the formula follow this procedure:
`3y-2x=8`
Add `2x` to both sides
`3y-2x+2x=8+2x`
`3y=8+2x`
Divide both sides by 3
`(3y)/3=(2x+8)/3`
Therefore: `y=2/3x+8/3`
Answer:
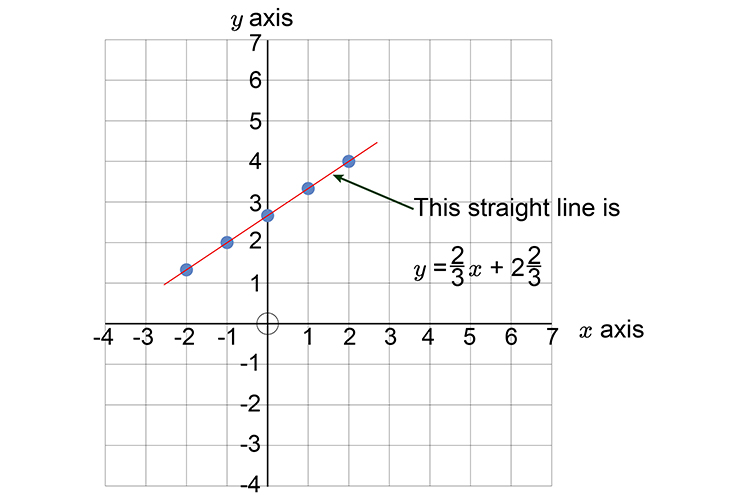
`y=2/3x+2\2/3`
This line can now be plotted on a graph as follows:
First let's calculate some points on the graph.
If
| `x=-2` | then `y` | `=2/3(-2)+2\2/3` | `=1.33` |
| `x=-1` | then `y` | `=2/3(-1)+2\2/3` | `=2` |
| `x=0` | then `y` | `=2/3(0)+2\2/3` | `=2.66` |
| `x=1` | then `y` | `=2/3(1)+2\2/3` | `=3.33` |
| `x=2` | then `y` | `=2/3(2)+2\2/3` | `=4` |
Now draw the graph and mark out the above points:
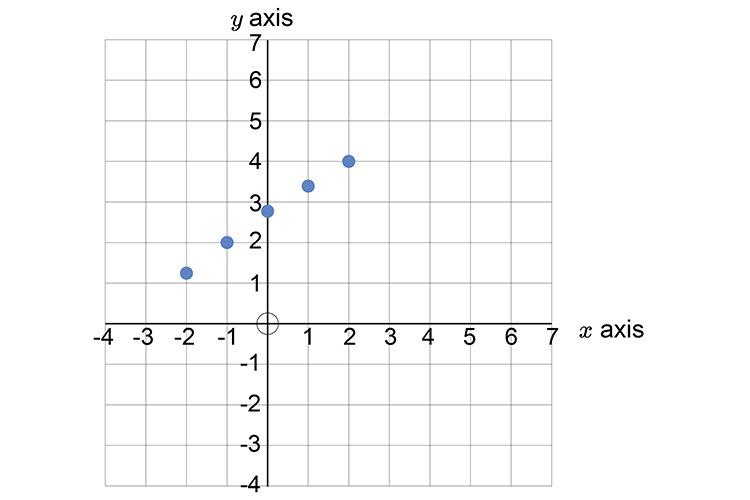
Now draw a straight line through these points.