Further explanation

Gradients	UPHILL is POSITIVE
	DOWNHILL is NEGATIVE

But you don’t need to remember this because it becomes obvious when you start to measure from the left hand side.

Example

Work out the gradient of the following straight lines.

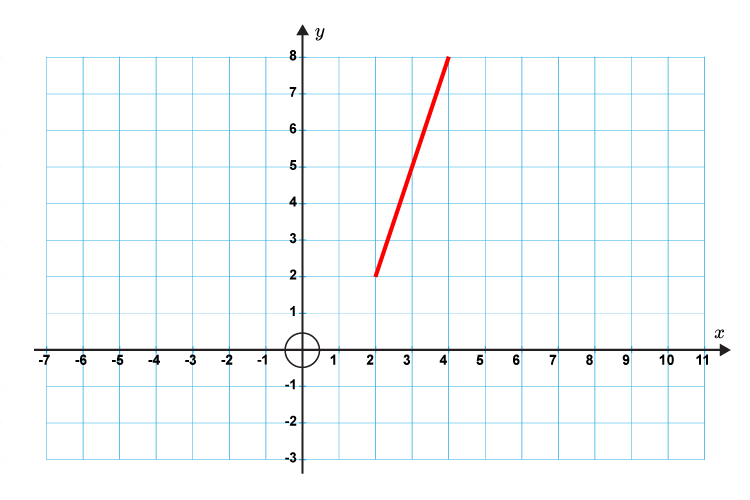
Work out this lines gradient

Where do we start from?

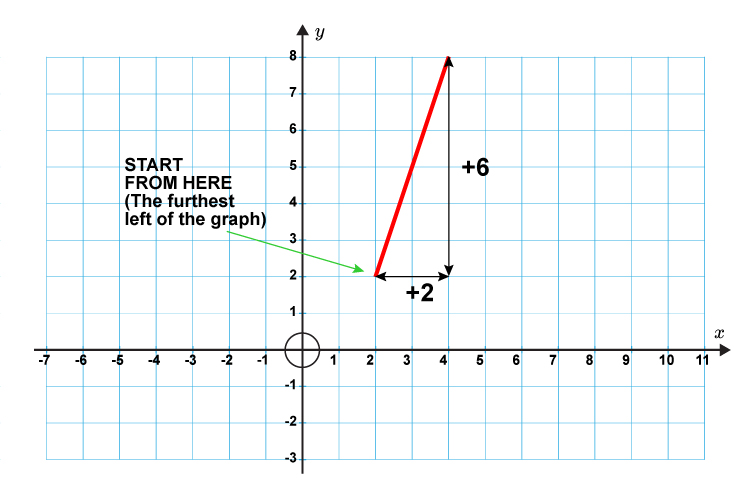
Start from the left and work your way up

`Gradient\ (m)=(y(chang\e\ i\n))/(x(chang\e\ i\n)`

`Gradient\ (m)=6/2=3`

Example

Work out the gradient of the following straight lines.

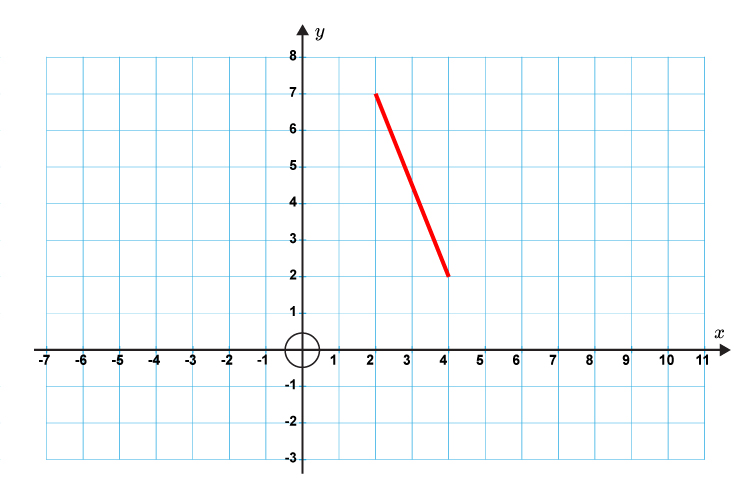
Work out this lines gradient

First, work out where we start from, then work out the horizontal `(x)` and vertical `(y)` points.

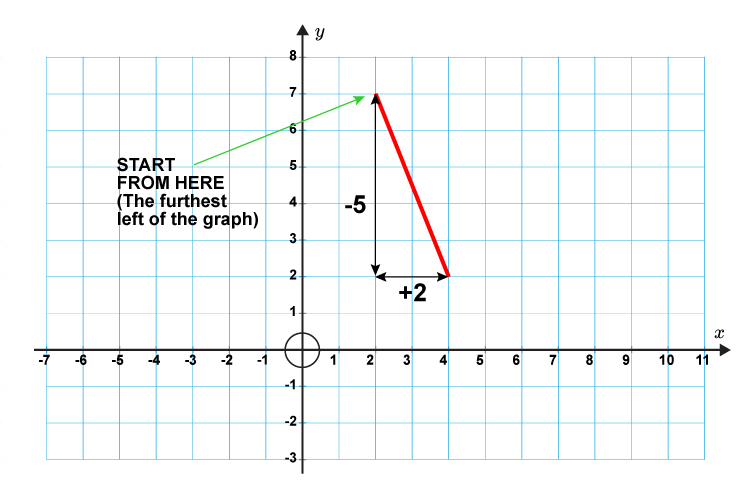
Start from the left and work your way down

`Gradient(m)=(y(chang\e\ i\n))/(x(chang\e\ i\n)`

`Gradient(m)=(-5)/2=-2.5`