Lens equation – Concave lens and examples

The lens equation is:

$1/F=1/(do)+1/(di)$

Where

$F$	$=$	Principal focal length

$do$	$=$	Object distance

$di$	$=$	Image distance

But to continue, we need to be careful and clear in our understanding of what is negative and what is positive.

Concave single lens

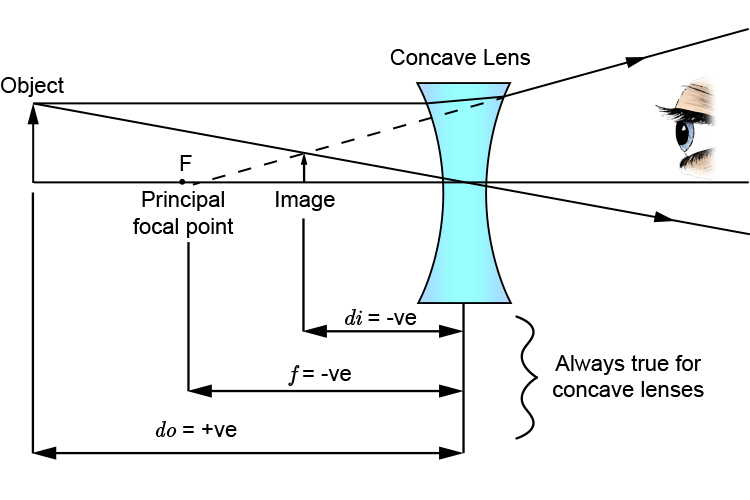
In all cases and situations of the concave lens the image will always be.

SMALLER

UPRIGHT

VIRTUAL (cannot be projected on a screen)

Between principal focal point and the concave lens

and to this list we should now add:

Concave lens and the lens equation image distance always negative

Single concave lens ray diagram

Examples

Question 1

If an object is $12cm$ from a concave lens with a focal length of $-6cm$ what is the image distance from the lens and is the image upright or upside down?

Answer

Immediately we see a minus principal focal length (we presume this is what the person who set the exam paper means by just saying focal length) then we know we must be dealing with a concave lens.

Knowing we are dealing with a concave lens we know the image will be upright.

Draw a quick sketch to remind ourselves:

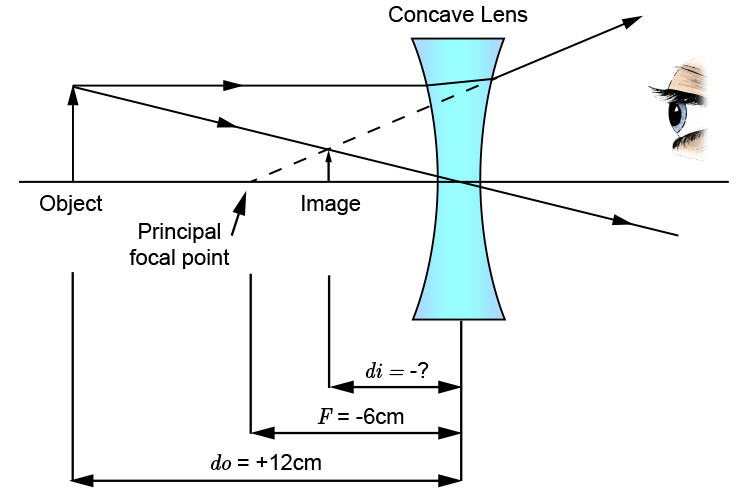
Concave lens ray diagram for question 1

From this quick reminder we have

$1/F=1/(do)+1/(di)$

$1/-6=1/12+1/(di)$

$-0.16dot6=0.083dot3+1/(di)$

$1/(di)=-0.25$

Multiply both sides by $di$ and divide both sides by $-0.25$ to get $di$ on its own.

$1/-0.25=di$

$di=-4$

and looking at the sketch we know all concave images are upright.

Answer = $-4$ and UPRIGHT

Question 2

A concave lens of focal length $15cm$ forms an image $10cm$ from the lens. How far is the object from the lens?

Answer

As we are given the fact that this is a concave lens we should draw a quick sketch to remind ourselves.

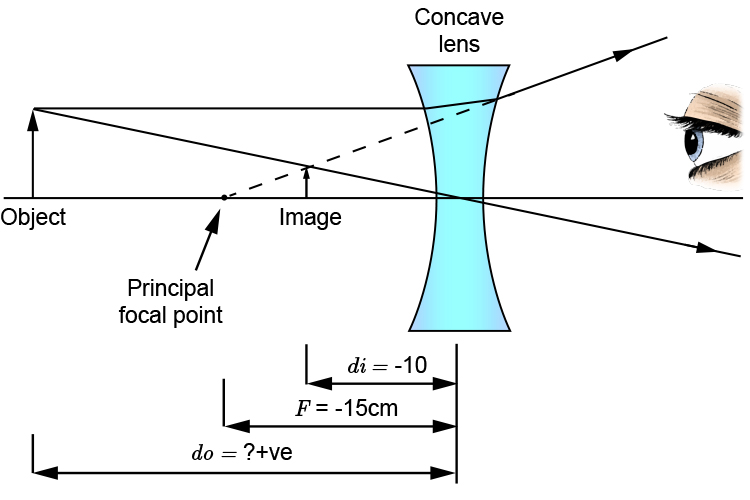
Question 2 concave lens ray diagram

We have to assume two things

i. When focal length of $15cm$ is mentioned we must assume that this means principal focal length and being a concave lens the focal length must be $-15cm$

ii. Although an image is formed at $10cm$ because this is a concave lens this must be $-10cm$

From this quick sketch we can follow with the lens equation which gives us.

$1/F=1/(do)+1/(di)$

$1/-15=1/(do)+1/-10$

$-0.066dot6=1/(do)-0.1$

$1/(do)=-0.066dot6+0.1$

$1/(do)=0.0333$

Multiply both sides by $do$ and divide both sides by $0.0333$ to get $do$ on its own.

$1/0.0333=do$

$do=30cm$

Example 3

A nail is placed a distance of $40cm$ from a diverging lens and an image is produced at a distance of $10.91cm$ from the lens. What is the distance of the principal focal point from the lens?

Answer

As soon as we can, when we read that there is a diverging lens we should draw a quick sketch to remind ourselves of the details of this lens:

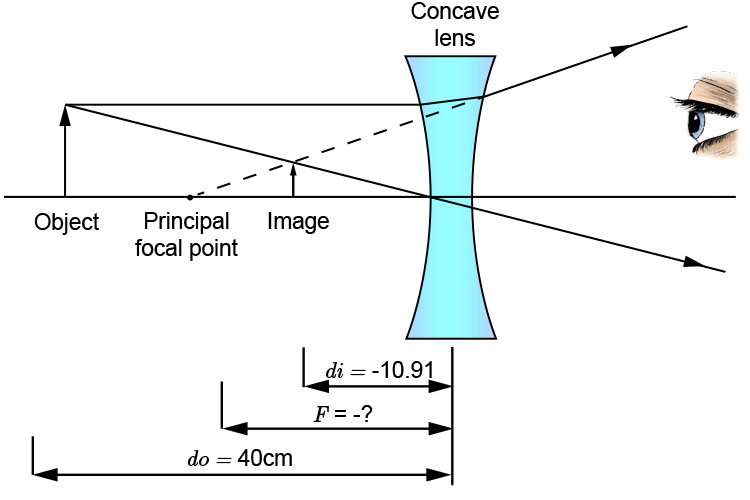
Question 3 concave lens ray diagram

We should realise that the image distance is not just $10.91cm$ but minus $10.91cm$ . We should also realise that the answer we are seeking should provide us with a minus number for the focal point.

Now we should recall the lens formula:

$1/F=1/(do)+1/(di)$

$1/F=1/40+1/-10.91$

$1/F=0.025-0.091659$

$1/F=-0.066659$

Multiply both sides by $F$ and divide both sides by $-0.66659$ we get.

$F=1/-0.066659$

$F=-15$

As we hoped, we get a minus principal focal length of $-15$