Practical ways to find the principal focal length of a concave lens using a convex lens

This section is purely to note that there are other ways to find the principal focal length of a concave lens. This definitely won't be tested in an exam at this level.

As a concave lens always forms a virtual image, its principal focal length cannot be found directly like a convex lens. We therefore have to find an indirect way. 

This is achieved by using a convex lens:

The first stage is to produce an image on a screen using a convex lens (see Mammoth Memory and the convex lens) which has a principal focal length of 10cm, as follows:

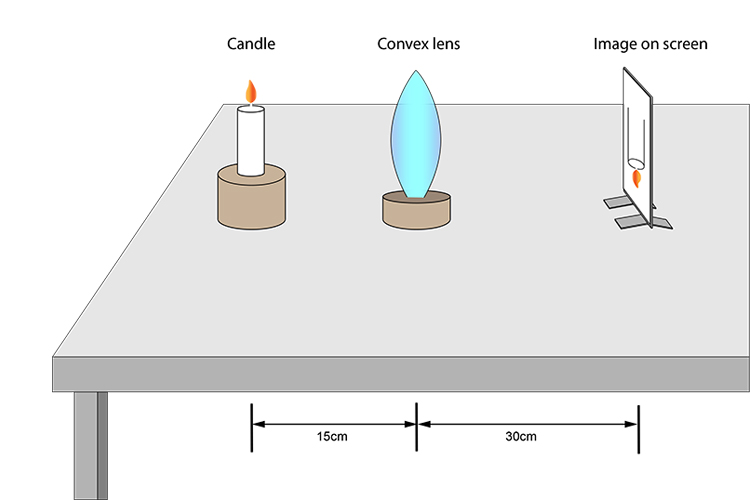
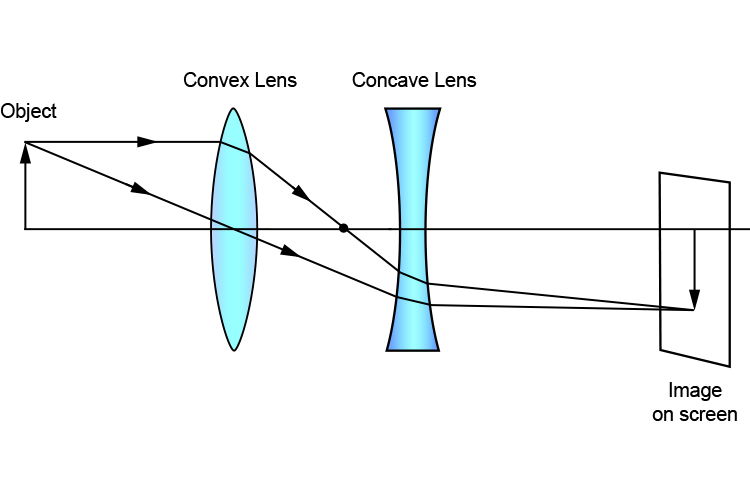
Now place a concave lens (whose principal focal length we don't know) in between the convex lens and the screen. You will then have to move the screen until you have a new image.

See below:

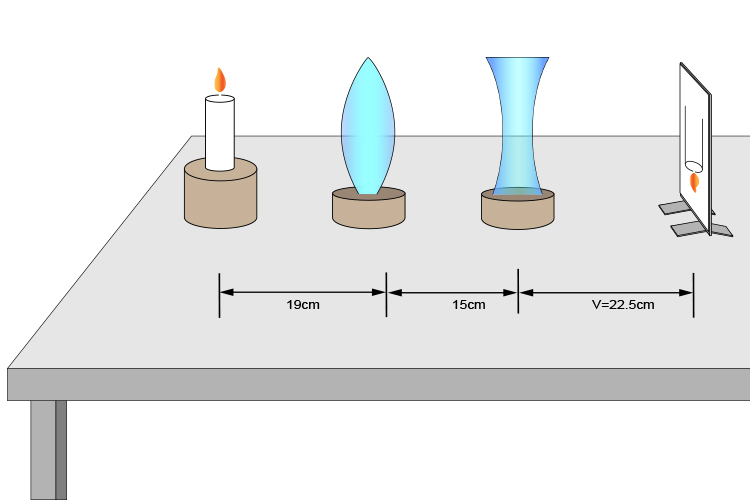
You always have to bear in mind where the convex lens produced the first image.

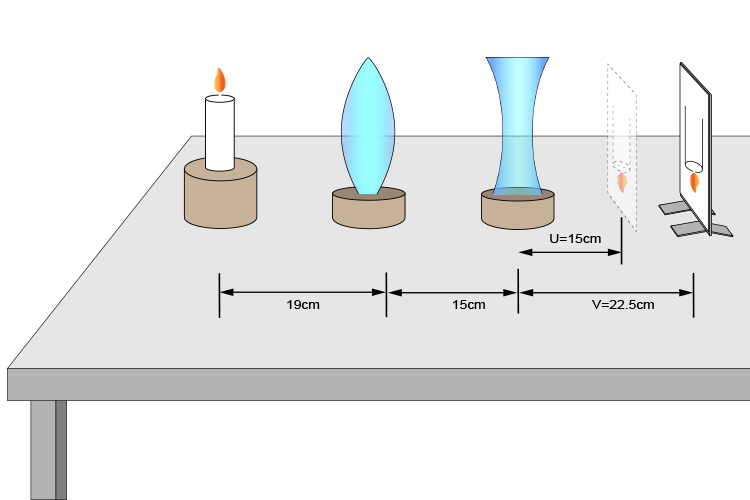
You can move the concave lens to several positions and record the values of `U` and `V` as follows:

		`U`	`V`
	1	15	22.5
	2	17.5	27.3
	3	19	32.9
	4	21	39.4
	5	23	47

You can then use the following formula to find the principal focal length of the concave lens as:

`F=(UV)/(U-V)`

(Again we emphasise strongly that you won't use this in an exam at this level. It's only being used to demonstrate how the concave principal focal length can be found).

So the chart would continue as follows:

		`U`	`V`	`F=(UV)/(U-V)`
	1	15	22.5	-45
	2	17.5	27.3	-45
	3	19	32.9	-45
	4	21	39.4	-45
	5	23	47	-45

So you can see that the principal focal length of the concave lens is 45cm.

NOTE: This only works if the converging power of the convex lens is greater than the diverging power of the concave lens because this still needs to work as a converging combination. Another way of putting this is that the focal length of the convex lens should be smaller than the focal length of the concave lens.

 

In ray diagram format, the above would look as follows:

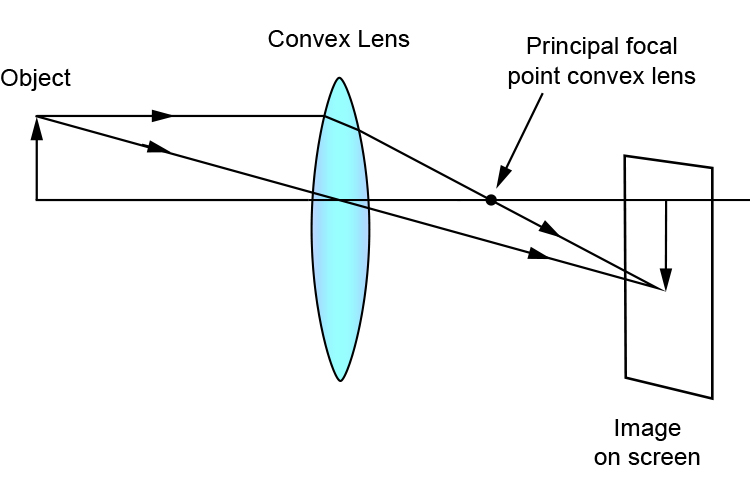
Again we emphasise that you will not be tested on this at this level of exam.

More Info