Convex mirrors and objects larger than the mirror
So far all of our objects have been smaller than the convex mirror. What happens when the object is larger than the convex mirror?
We can use the laws of reflection.
For reference see the section Using the law of reflection – ray diagram rules.
The same method can be adopted here.
NOTE: The main law of reflection we are using here is: "The angle between the incident ray and the normal is equal to the angle between the reflected ray and the normal."
See below.
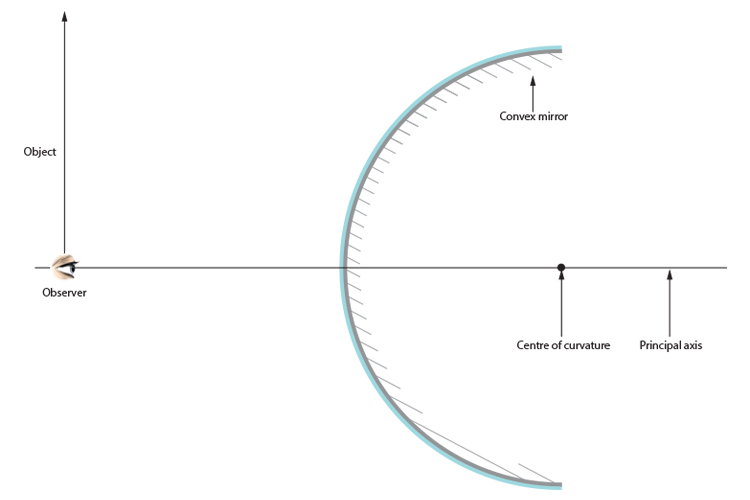
Make the observer sit on the principal axis in line with the centre of curvature.
Place a protractor with the straight edge against the convex mirror. Use a ruler to extend the protracted lines. Move the protractor around the outside edge of the convex mirror until you have the point of the arrow (the incident ray) and the observer (reflected ray) with an equal angle between these rays and the 90° mark on the protractor. Always keep the protractor at a tangent to the convex mirror.
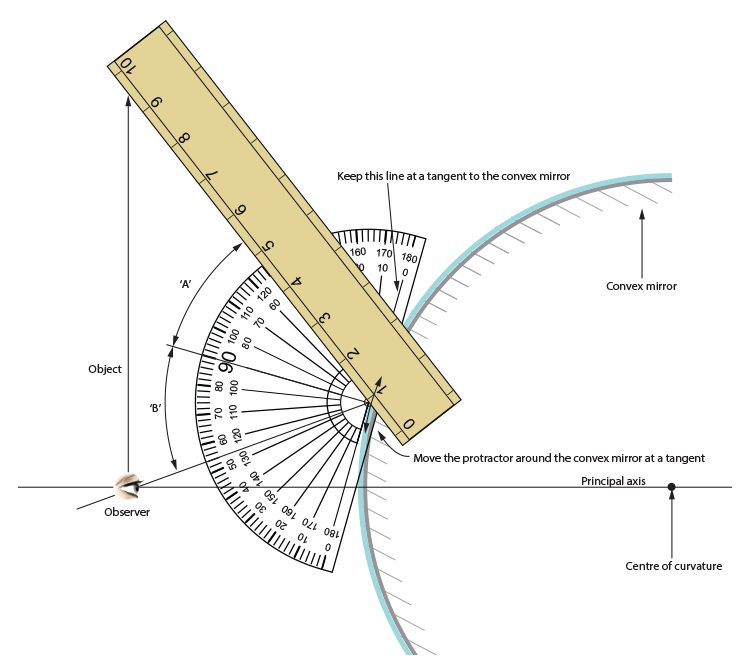
Move the protractor until these two angles "A" and "B" are the same.
When the angle between the incident ray and the normal is equal to the angle between the reflected ray and the normal we can then mark a dot on the outside edge of the protractor where this occurs.
You can then draw the incident ray to the mirror and the reflected ray to the observer.
The bottom of the arrow (object) at the point nearest to the principal axis, will have the incident ray and the reflected ray in the same plane.
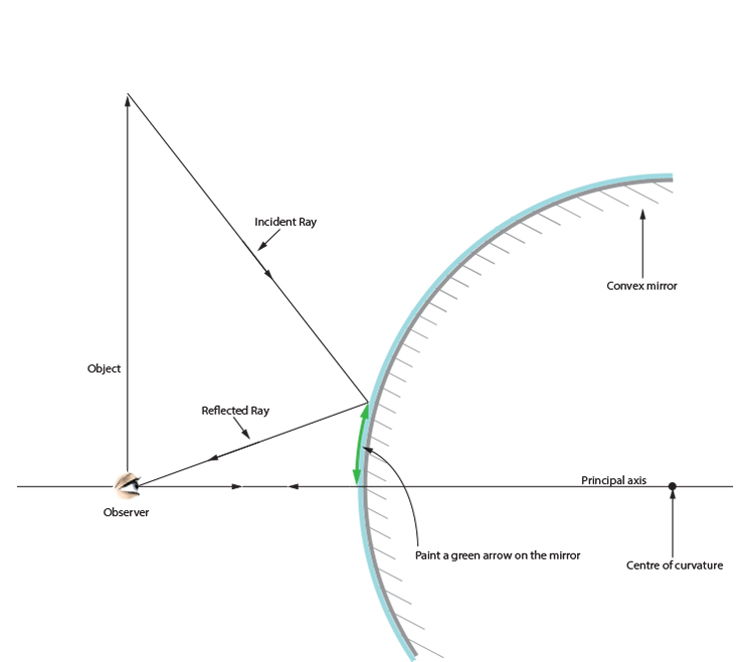
If you could ask someone to paint, in green, where the arrow was on the convex mirror it would look like the above diagram.
If you removed the object and left the green arrow it would look like the original object was still there.
The object, even a much larger one, is always smaller in a convex mirror see below:





