Interpreting parabola formulas

The general formula for a parabola is $ax^2+bx+c=y$

Positive and negative $x^2$ coefficients

If $x^2$ is positive then your parabola will look like this:

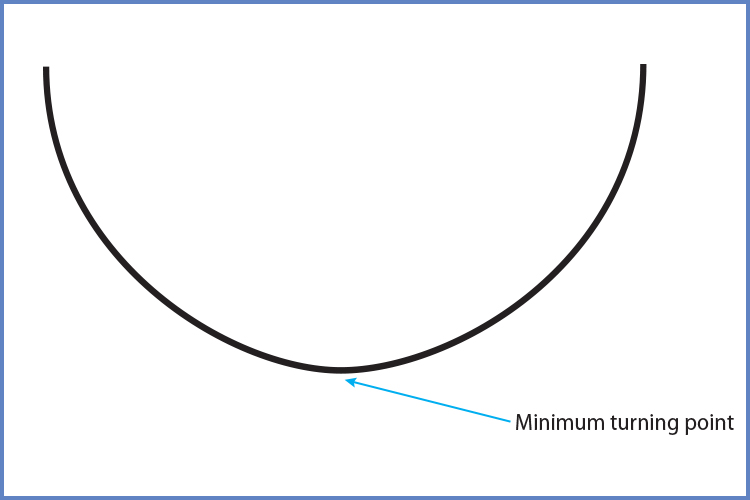
A positive parabola will look like this

If $x^2$ is negative then your parabola will look like this:

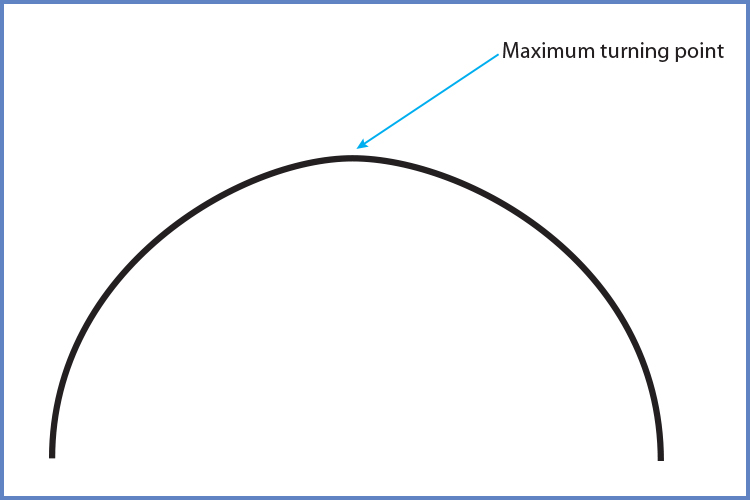
A negative parabola will look like this

NOTE:

See later on finding the solution is finding the root or roots which is where the curve passes the $x$ axis.

If in finding the solution to $ax^2+bx+c=y$

$x=+-sqrt(-12)$ (for example)

It's not possible to find the square root of a negative number.

(To prove this put 3 then minus 6 into your calculator and then press the root button. You will get an error message.)

You are unable to find the root of a negative number

Your parabola will look something like the diagram below, meaning that the curve doesn't cross the $x$ axis.

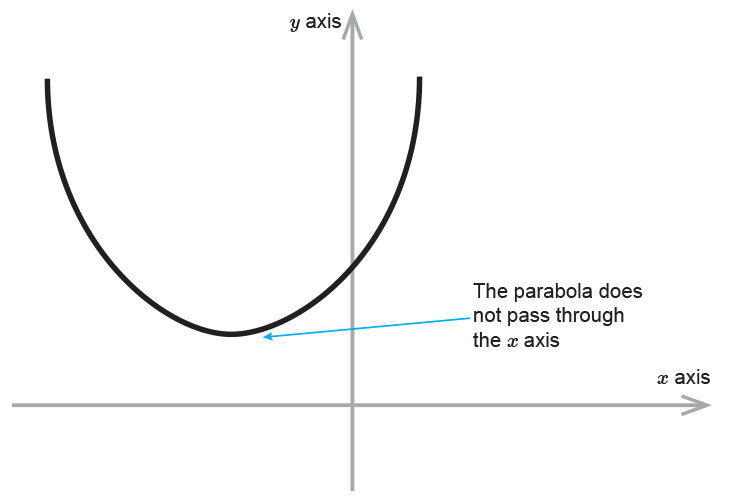
A negative parabola is not possible because it doesn’t go through the x axis

NOTE:

$x=+-sqrt(-12)$ is called "Quadratics and complex numbers" and if you found this in an exam at this stage you've done something wrong.

If in finding the solution to:

$ax^2+bx+c=y$

$x=3$ (for example)

And NOT $x=-1\ \ \ and\ \ \ 2$

Then your parabola will be turning on the $x$ axis as follows:

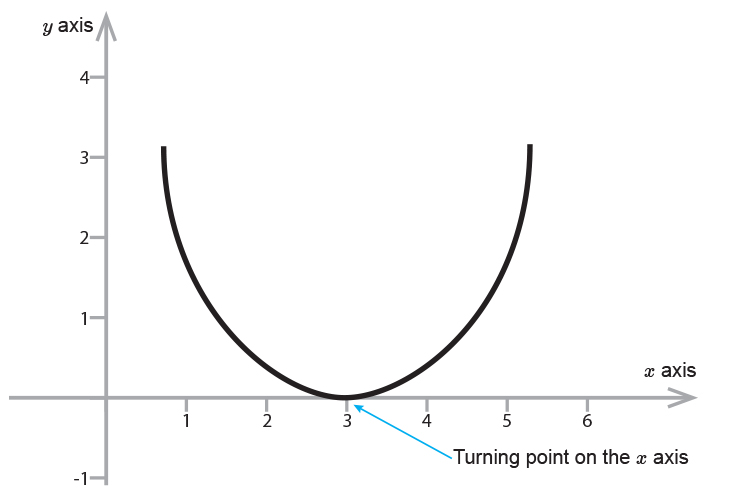
A positive parabola will always touch or go through the x axis

$x=3$ Would mean the parabola touches the $x$ axis at $x=3$ only, once.