Parabolas

The general form of a parabola is:

`ax^2+bx+c=y`

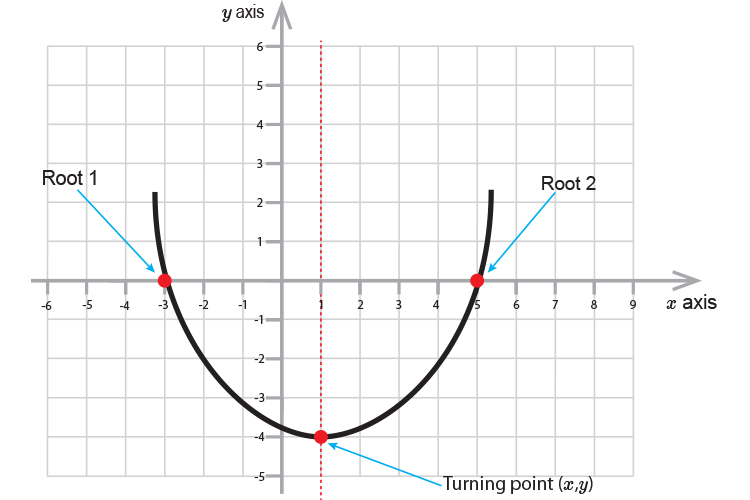
And may look like the following graph:

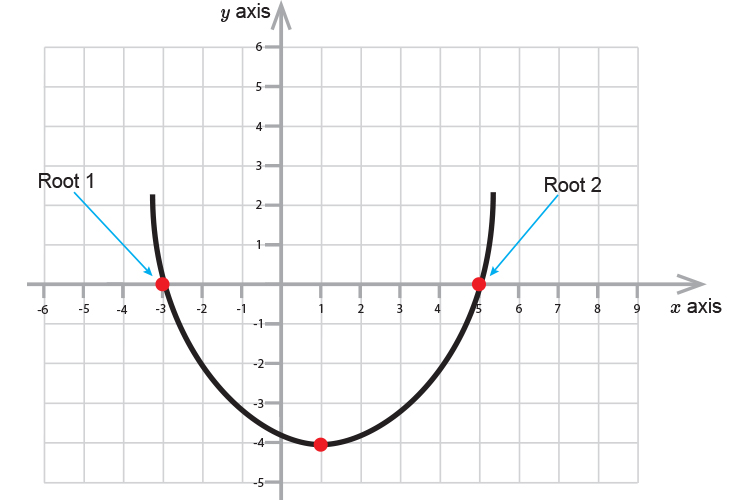
Parabolas x roots are shown on the x axis

If `y=0` (i.e. where the parabola passes through the axis), then

`ax^2+bx+c=0`

We have various ways to work out these points (or roots).

You often get asked in an exam to solve a quadratic equation like

`3x^2-7x+2=0`

This really means that you find the roots of the curve.

The way to solve `x` (or find the roots) include:

1. Substituting values of `x` and drawing a curve

2. Completing the square

3. Quadratic equation

4. Factorising quadratic equation

Finding roots helps because if you halve the distance between the roots this will provide you with the turning point of the parabola.

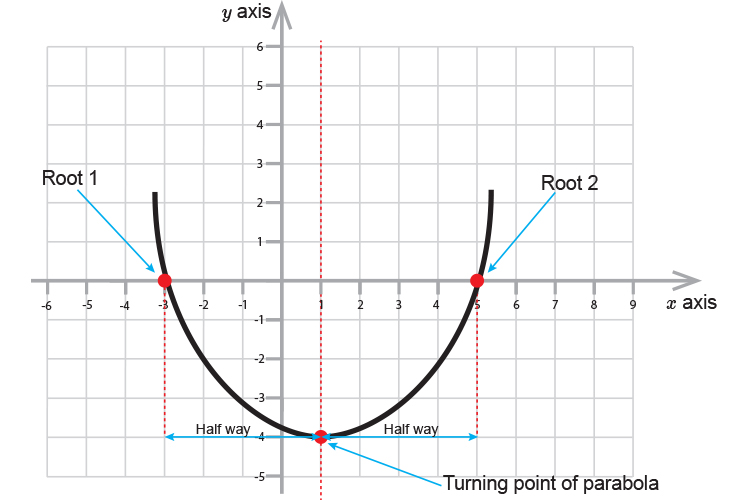
The turning point of a parabola is half way between each root

If you find the value of `x` at the half way point and plug this value back into `ax^2+bx+c=y` this will provide you with the value of `y` at the turning point.

For any general form

`ax^2+bx+c=y`

if you can work out the roots of `x` you can plot several points of a parabola (including root1, root2 and the turning point `(x,y)\)`.

The turning point is equal to xy as it is where both axis meet