Substituting values of x
For many quadratic equations they can actually be solved by substituting values of x into the equation and then drawing the graph.
If you have time our advice is:
Always do a quick sketch
Example 1
Solve `x^2+3x-4=y`
| `x=2` | `2^2+3times2-4` | `=` | `4+6-4` | `=6` |
| `x=1` | `1^2+3times1-4` | `=` | `1+3-4` | `=0` |
| `x=0` | `0^2+3times0-4` | `=` | `0+0-4` | `=-4` |
| `x=-1` | `(-1)^2+3times(-1)-4` | `=` | `1-3-4` | `=-6` |
| `x=-2` | `(-2)^2+3times(-2)-4` | `=` | `4-6-4` | `=-6` |
| `x=-3` | `(-3)^2+3times(-3)-4` | `=` | `9-9-4` | `=-4` |
| `x=-4` | `(-4)^2+3times(-4)-4` | `=` | `16-12-4` | `=0` |
| `x=-5` | `(-5)^2+3times(-5)-4` | `=` | `25-15-4` | `=6` |
If we plot these coordinates on a graph we get:
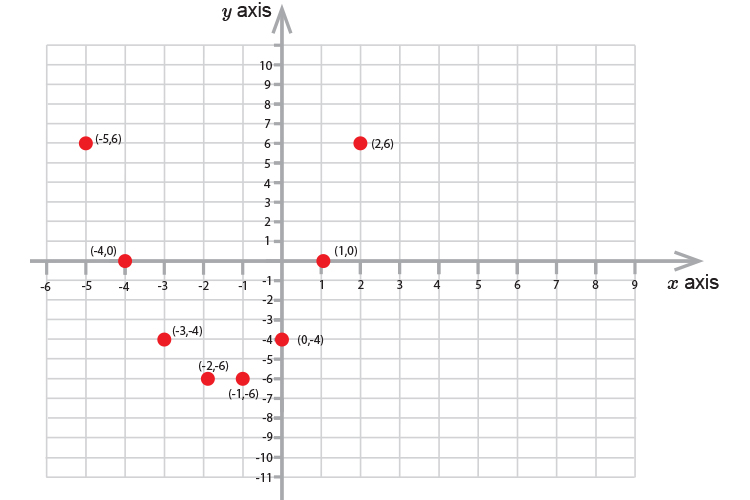
Now joining up the points we get:
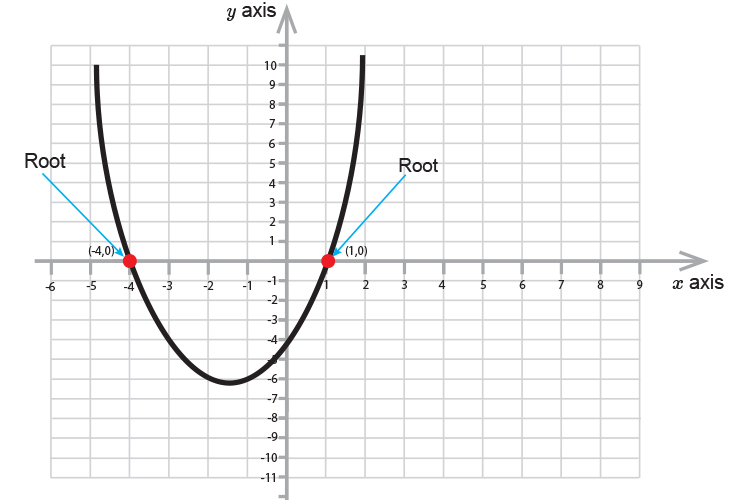
Here we can see that the roots are `+1` and `-4`
So why do we not use this way always?
Because you might get a beast like:
`2x^2-5x-6=y`
Try plotting this one:
| `x=4` | `2times4^2-5times4-6` | `=` | `32-20-6` | `=6` |
| `x=3` | `2times3^2-5times3-6` | `=` | `18-15-6` | `=-3` |
| `x=2` | `2times2^2-5times2-6` | `=` | `8-10-6` | `=-8` |
| `x=1` | `2times1^2-5times1-6` | `=` | `2-5-6` | `=-9` |
| `x=0` | `2times0^2-5times0-6` | `=` | `0-0-6` | `=-6` |
| `x=-1` | `2times(-1)^2-5times(-1)-6` | `=` | `2+10-6` | `=6` |
If we plot these coordinates on a graph we get:
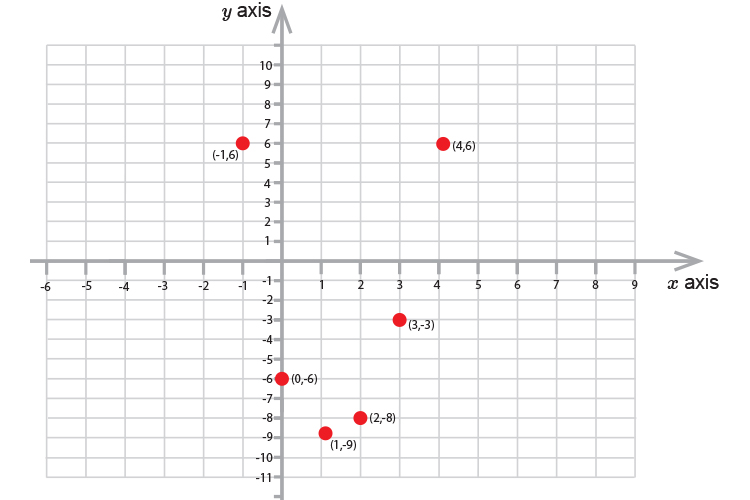
Now joining up the points we get:
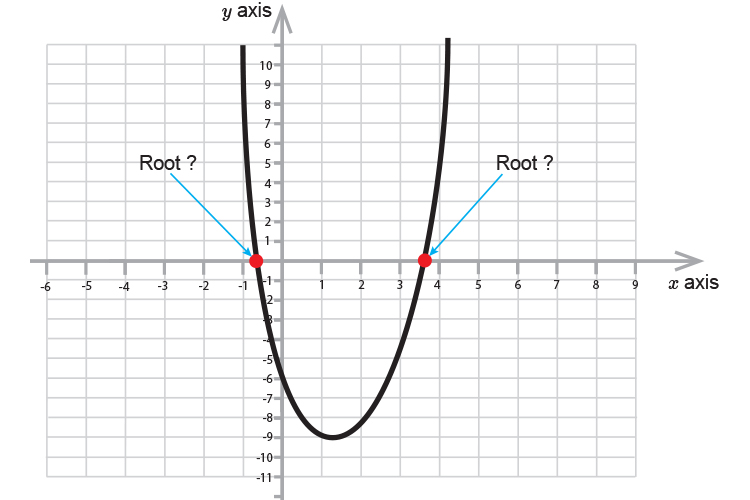
You can see that you can not find the roots graphically.
But you can find them using the quadratic formula.
Example 2
Solve `2x^2-5x-6=y` using the quadratic formula.
The quadratic formula is:
`x=(-b+-sqrt(b\ ^2-4ac))/(2a)`
In this case `a=2`, `b=-5` and `c=-6`
`x=(-(-5)+-sqrt((-5)^2-4times2times(-6)))/(2times2)`
`x=(5+-sqrt(25+48))/4`
`x=(5+-sqrt73)/4`
`x=(5+sqrt73)/4 \ \ \ or \ \ \ x=(5-sqrt73)/4`
`x=3.386 \ \ \ or \ \ \ x=-0.886`
`




