Examples using lens equation
Example 1
How far is the image produced from the centre line of a convex lens if an object is placed 4cm away from this convex lens of focal length 8cm?
Answer:
First, we must assume that focal length of 8cm means the principal focal length is 8cm.
We should have drawn three quick convex lens sketches (see Mammoth Memory – Convex lens – What to do in an exam).
The sketch we need is:
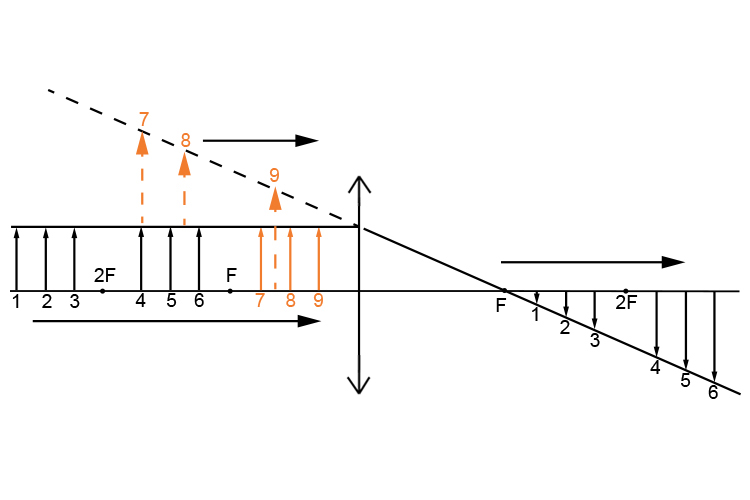
We can see immediately that when the object is placed between the lens and `F` (the principal focal length) then the image is going to be:
| Same side as object | |
| Upright | image |
| Image | larger |
| Image | virtual |
However, let's see what the lens formula gives us.
`1/F=1/(d\o)+1/(d\i)`
`1/8=1/4+1/(d\i)`
`0.125=0.25+1/(d\i)`
`0.125-0.25=1/(d\i)`
`1/(d\i)=-0.125`
Multiply both sides by `d\i` and divide both sides by `-0.125` to get `di` on its own we have:
`1/-0.125=d\i`
`d\i=-8`
The image distance is minus 8cm.
This would look like the following:
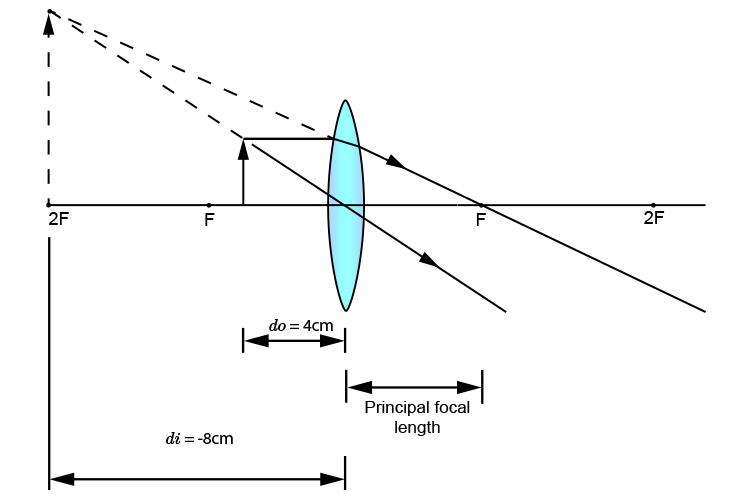
Our sketch and concluded drawing agree and we can therefore see this is a magnified image.
Example 2
A converging lens has a focal length of 10cm. If a light is located 30cm from the lens, what type of image will be formed and where will it be located?
Answer:
The first thing to recognise is that a converging lens is a convex lens.
From the three quick convex lens sketches (see Mammoth Memory – What to do in an exam), the sketch we need is:
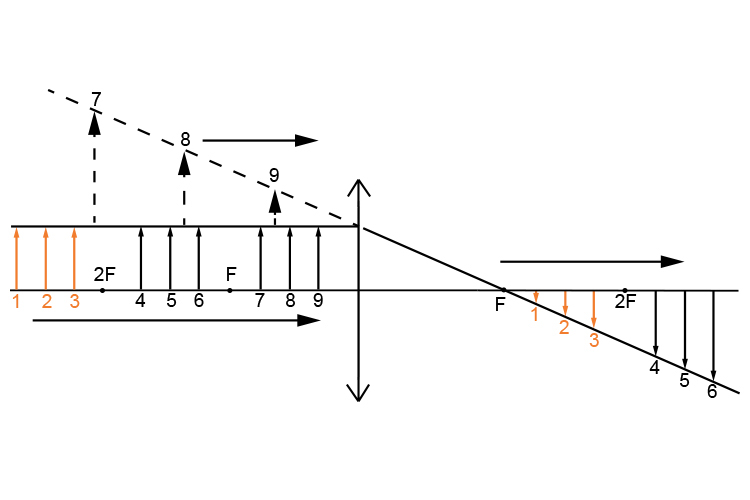
We can see from this sketch that if the principal focal length is 10cm and the object is 30cm from the convex lens then the image will be further away than `2F` (see point 1, 2 or 3) and will be real and inverted.
This will be a great help to us in the calculated answer.
Lens formula gives
`1/F=1/(d\o)+1/(d\i)`
`1/(10cm)=1/(30cm)+1/(d\i)`
`0.1=0.03dot3+1/(d\i)`
`0.1-0.03dot3=1/(d\i)`
`1/(d\i)=-0.06dot6`
Multiply both sides by `d\i` and divide both sides by `0.06dot6` to get `di` on its own, we have:
`1/(0.06dot6)=d\i`
`d\i=15cm`
If we sketch the resultant ray diagram we would get:
Our sketch and concluded diagram concur and therefore we can see that the image is:
Smaller
Inverted
Real
Example 3
An object 25cm away from a lens produces a focused image on a screen 15cm away. What is the focal length of the converging lens?
Answer:
With the words "converging lens" we know we are talking about a convex lens.
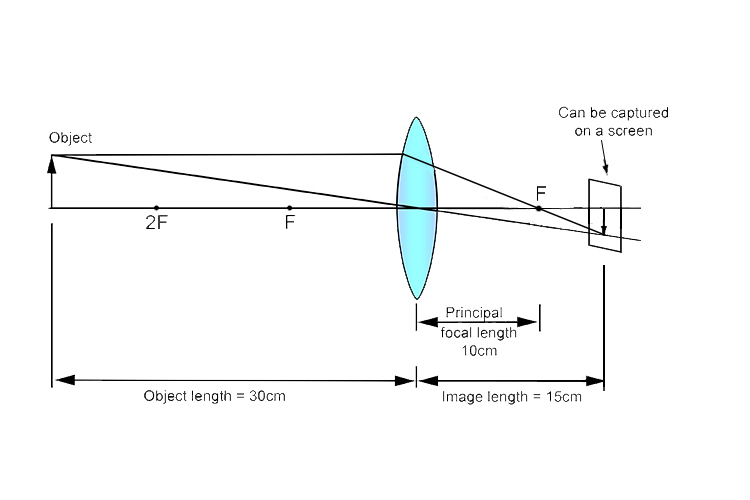
If we draw out the best sketch to use as a reminder we have:
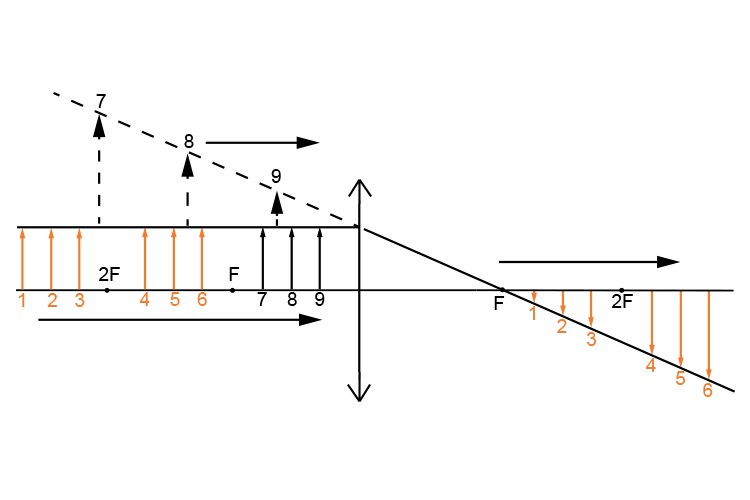
Although this ray diagram sketch doesn't give us an exact answer we know that in order for an image to be created the object will be at the first set of numbers between 1 and 6 and the image will be on the other side of the lens again between 1 and 6.
So we can glean from this that the image is:
Real
Inverted
but the image could be smaller or larger than the object. From the sketch we also know that `d\i` is +ve therefore using lens formula we get:
`1/F=1/(d\o)+1/(d\i)`
`1/F=1/25+1/15`
`1/F=0.04+0.066dot6`
`1/F=0.106dot6`
Multiply each side by `F` and divide each side by `0.106dot6` to get `F` on its own, we get::
`F=1/(0.106dot6)`
`F=9.375`
`F~~9.4`
If we sketch the resultant ray diagram we get:
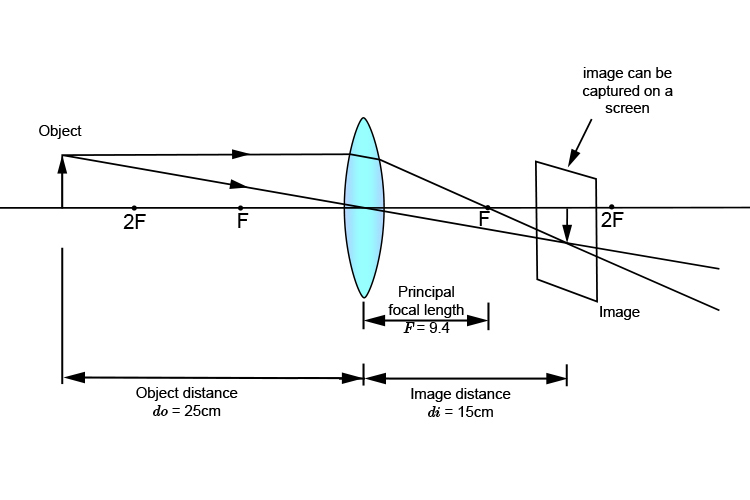
We can see the image is:
Real
Inverted
Smaller than the original




