Practical ways to find the principal focal length - lens equation

There is another way to find the principal focal length of a convex lens but unfortunately, we have to learn another equation, the lens equation.

But it is really easy to remember using the following mnemonic:

Lens equation
IF I DO I DIE

$I/F=I/(do)+I/(di)$

$1/F=1/(do)+1/(di)$

The lens equation is:

$1/F=1/(do)+1/(di)$

Where

$F$	$=$	Principal focal length

$do$	$=$	Object distance

$di$	$=$	Image distance

Place a burning candle at one end of a table, a convex lens in the centre of the table and a screen at the other end of the table.

Move the screen and convex lens backwards and forwards on the table until a sharp upside-down image of the burning candle is made.

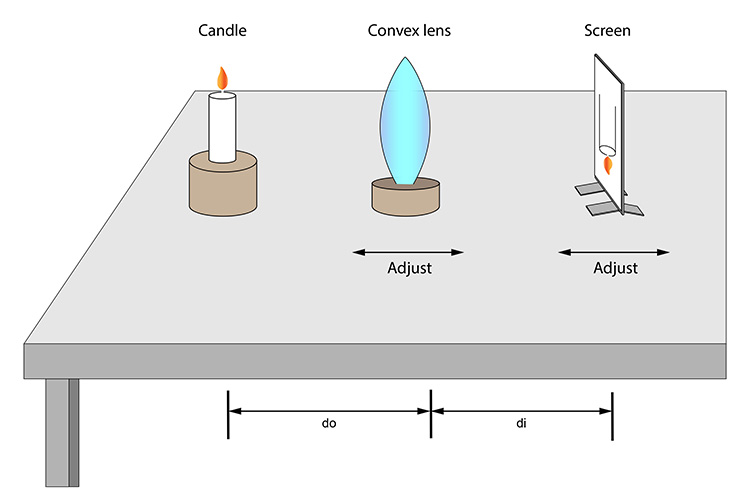
Setting out a candle convex lens and screen to find the principal focal length

Once you have a sharp upside-down image on the screen you can measure $do$ and $di$ and put the figures into the formula.

$1/F=1/(do)+1/(di)$

and work out the principal focal point $F$ .

In ray diagram format that would be:

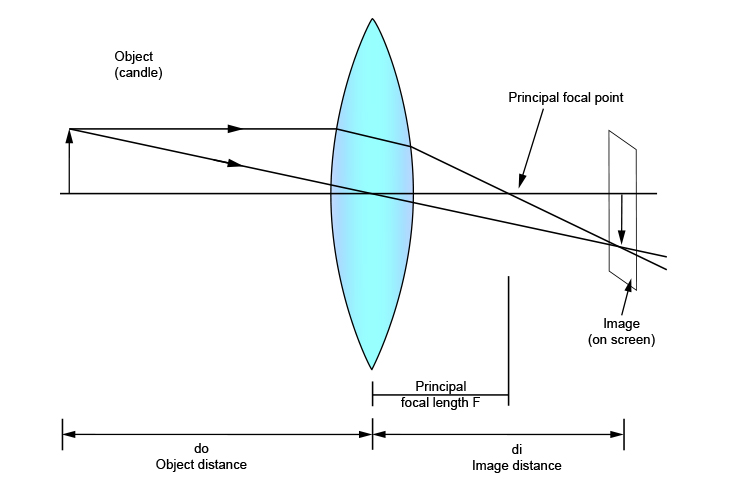
Convex lens ray diagram showing the principal focal point and principal focal length

An example would be:

Question 1

In the experiment below an upside down image of the candle has been clearly formed on the screen. What is the convex lens's principal focal length?

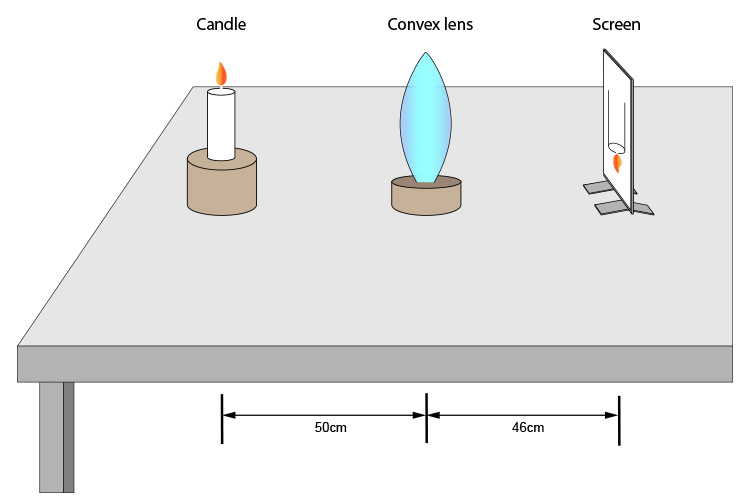
Finding the convex lenses principal focal length when 50cm from a candle

Using the lens equation we have

$1/F=1/(do)+1/(di)$

$1/F=1/50+1/46$

$1/F=0.02+0.21739$

$1/F=0.041739$

$F=1/0.041739$

$F=23.96cm$

Question 2

Just to show you that this formula works in any unit, let's do the same experiment but measure the distances in mm. What is the principal focal length?

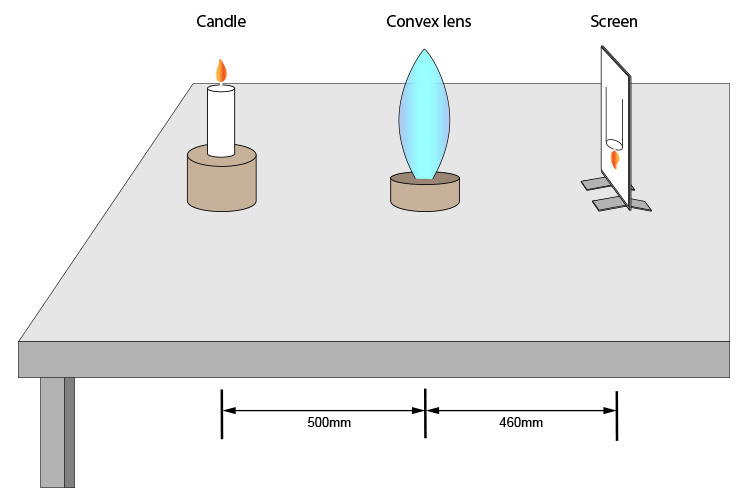
The units used to measure the distances in this experiment will not affect the answer you get using the formula

Using the lens equation we have.

$1/F=1/(do)+1/(di)$

$1/F=1/500+1/460$

$1/F=0.0041739$

$F=1/0.0041739$

$F=239.58mm$