Normal line – convex lens

Before we go any further, you need to understand what the normal line is in connection with convex lenses.

There are several definitions of the normal line of a convex lens.

1. Normal line is the line perpendicular (at 90°) to the tangent line.

Or

2. The normal line is an imaginary line at 90° to where the ray touches the surface.

NOTE: for explanation of tangent line see Mammoth Memory Maths.

But at Mammoth Memory we believe that the image you should think of is a bow held by a Norman warrior in which the bow is the curve and the arrow is the normal line.

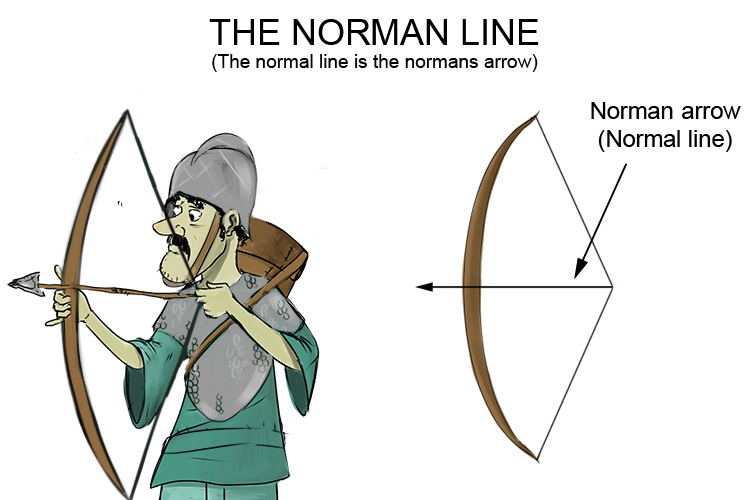
Norman warrior and his bow helps you remember the normal line.

The Norman's arrow is the line perpendicular (at 90°) to the tangent line of the bow. The arrow is the imaginary line at 90° to the bow.

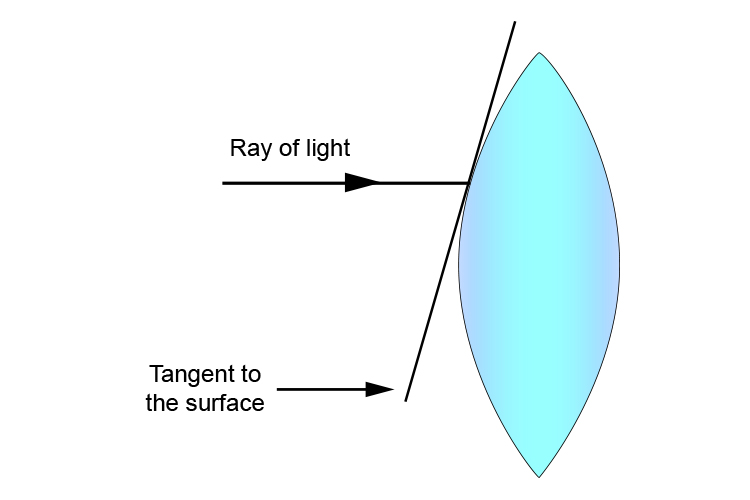
So, at the point where the ray touches the surface, of a convex lens, draw a tangent to the surface

Tangent on the surface of a convex lens

then draw a perpendicular line (at 90°) to the tangent.

The normal line is at 90° to the tangent

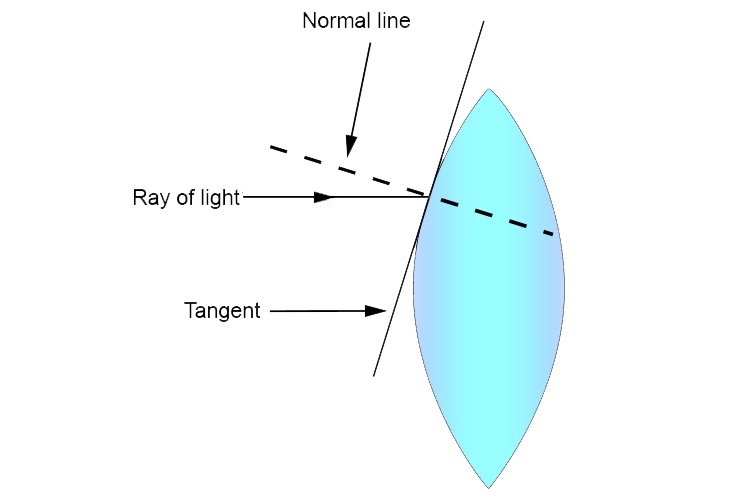
The Normal line is the arrow that would exist if the curve were the bow.

To complete the above diagram we can now remove the tangent line and we then get the following:

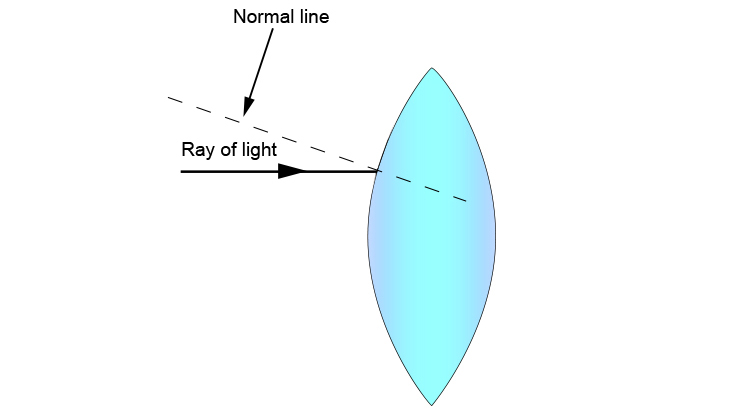
Normal line of a convex lens

This is the normal line and it is perpendicular to the convex lens surface drawn at the point of contact.

The ray of light will now refract (change direction) at the surface of the convex lens. For the rules of refraction and how much the ray of light bends see Mammoth Memory: Refraction.

Because at this level of physics we are only dealing with thin lenses the actual amount the light refracts (changes direction) across the lens is minimal. As long as the ray of light is shown to turn slightly towards the normal line on the diagram this will be sufficient for exam purposes.

NOTE: Most of the diagrams we show exaggerate the width of the lens for ease of explanation.

Once the ray of light is inside the lens, the rules of refraction again apply as the ray of light travels through the lens and approaches the exit surface. At the point where the ray touches the exit surface, draw a tangent to the outer surface:

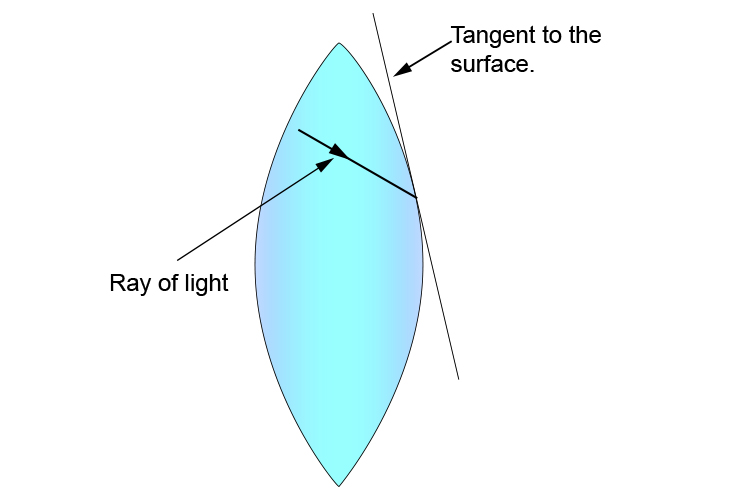
Tangent to surface 2 of a convex lens

then draw a perpendicular line (at 90°) to the tangent to find the normal line.

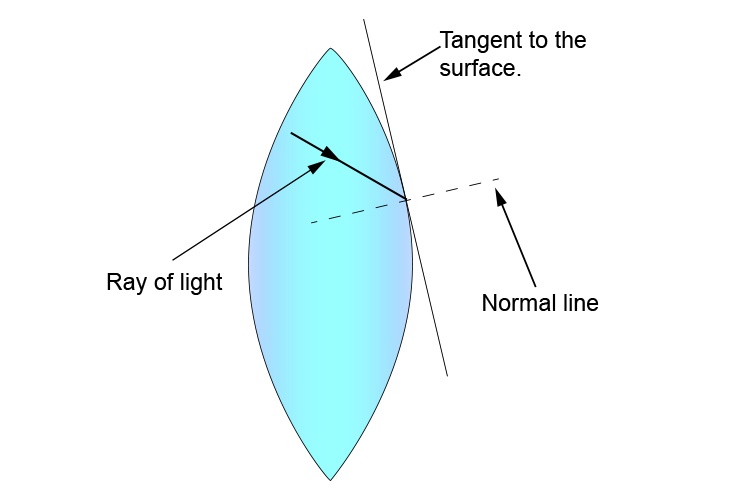
Normal line at 90° to the tangent

We can remove the tangent line and then we have the following:

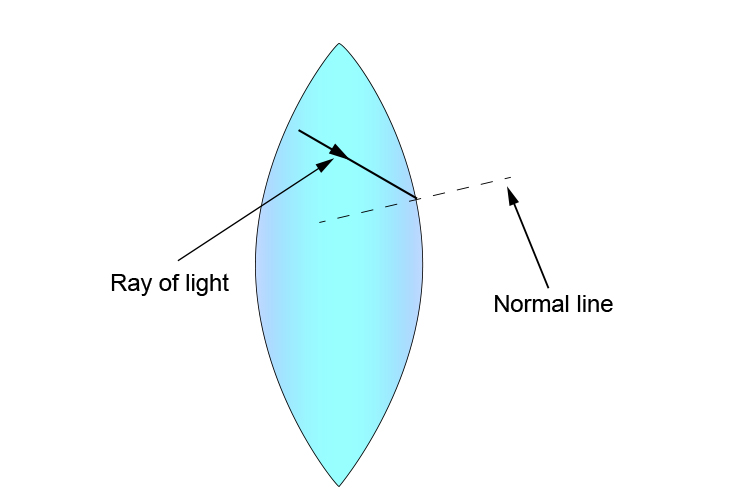
Normal line of surface 2 on a convex lens

Again, this is a normal line (there are two for each ray of light, one as it enters and another as it exits the lens), and it is perpendicular to the convex lens surface drawn at the point of contact.