Principal focal point and refractive index (`n`)

Unlike mirrors, different convex lenses of the same size (i.e. ones with the same centre of curvature which defines how curved the convex lens is) can have different principal focal points.

So much depends on the material the convex lens is made of and the angle of refraction that this creates. You have to know the refraction index of the material (`n`).

Example 1

$Ray diagram of a convex lens with a refractive index of 1.4$

Example 2

$Ray diagram of a convex lens with a refractive index of 1.8$

NOTE: For comparison, Air `n=1`, Glass `n=1.5`, Diamond `n=2.4`

$Higher refractive index = Shorter principal focal point$

This makes sense and should be easy to remember because the higher the refractive index the more the light ray refracts (see refractive index section).

Below are the figures used to work this out but they should not concern anyone at this level.

Example 1

Lens radius	`=`	`60mm`
Index of refraction	`n=`	`1.4`
Object position	`=`	`135mm\ \ \ (d\o)`
Object height	`=`	`60mm`
Gives
Image position	`=`	`168mm\ \ \ (d\i)`
Image height	`=`	`74mm`
Focal length	`=`	`75mm`

$Working out the principal focus length of a convex lens with a refractive index of 1.4$

Example 2

Lens radius	`=`	`60mm`
Index of refraction	`n=`	`1.8`
Object position	`=`	`135mm\ \ \ (d\o)`
Object height	`=`	`60mm`
Gives
Image position	`=`	`51mm\ \ \ (d\i)`
Image height	`=`	`22mm`
Focal length	`=`	`37mm`

$Working out the principal focus length of a convex lens with a refractive index of 1.8$

NOTE:

In some books you may read that the principal focal length of a lens is

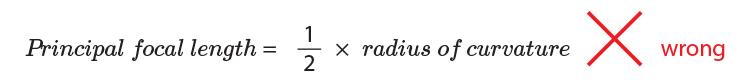
Incorrect principal focal length listed in some books

You can see from the above that this can not possibly be correct because for the same curvature lens different materials will have a different principal focal point, hence a different principal focal length.