Using the quadratic formula solver Example 1
Solve `3x^2-7x+2=0`
Use the quadratic formula solver
`x=(-b+-sqrt(b^2-4ac))/(2a)`
Therefore `a=3` , `b=-7` , & `c=2`
`x=(-(-7)+-sqrt((-7)^2-4times3times2))/(2times3)`
`x=(7+-sqrt(49-24))/6=(7+-sqrt25)/6=(7+-5)/6`
`x=12/6` and `x=2/6`
`x=2` and `x=1/3`
So `x=2` and `1/3` is the answer.
Now check this is correct
`3x^2-7x+2=0`
If `x=2` `3times2^2-7times2+2=0`
`12-14+2=0` Which is correct
If `x=1/3` `3times(1/3)^2-7times(1/3)+2=0`
`3/9-7/3+2=0`
`1/3-2\1/3+2=0` Which is correct
(If they don't add up to zero you can be assured that it is wrong).
Answer:
The roots of `3x^2-7x+2=0` are `x=2` or `1/3`
Quick stetch example 1
`3x^2-7x+2=0`
| `x=3` | `y=` | `3times3^2-7times3+2=` | `27-21+2` | `=8` | |
| `x=2` | `y=` | `3times2^2-7times2+2=` | `12-14+2` | `=0` | |
| `x=1` | `y=` | `3times1^2-7times1+2=` | `3-7+2` | `=-2` | |
| `x=0` | `y=` | `3times0^2-7times0+2=` | `0-0+2` | `=2` | |
| `x=-1` | `y=` | `3times(-1)^2-7times(-1)+2=` | `3+7+2` | `=12` |
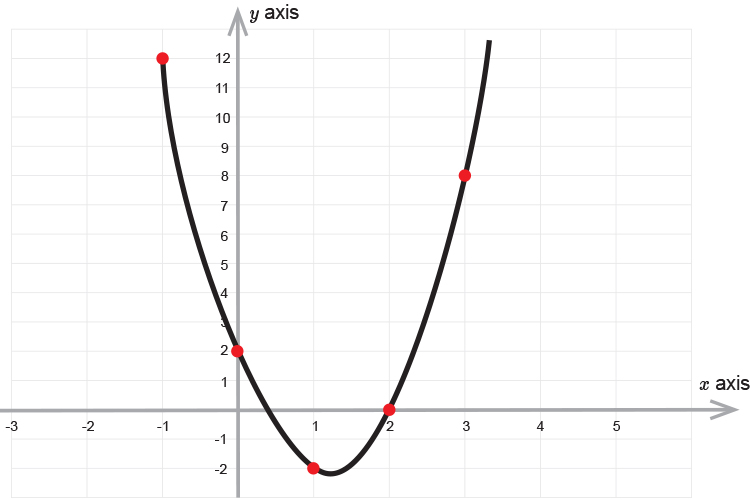
We have found one root as `x=2`




