Where does the quadratic formula come from?
NOTE:
You really don't need this: It's just for the maths purists.
Where does `x=(-b+-sqrt(b^2-4ac))/(2a)` come from?
We know the general formula for a quadratic equation is:
`ax^2+bx+c=0`
Solve using "completing the square method"
Complete the square `ax^2+bx+c=0`
NOTE:
In order to solve this the coefficient (or number) in front of the `x^2` must be a one.
So divide all sides by `a`
`(ax^2)/a+(bx)/a+c/a=0/a`
`x^2+(bx)/a+c/a=0`
Remember
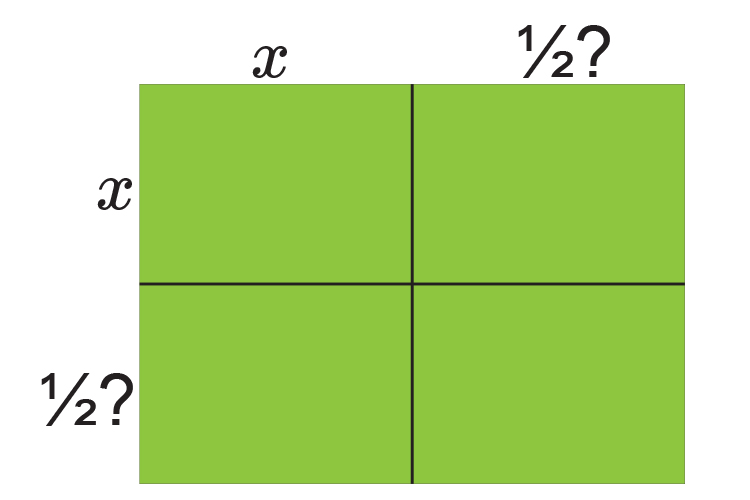
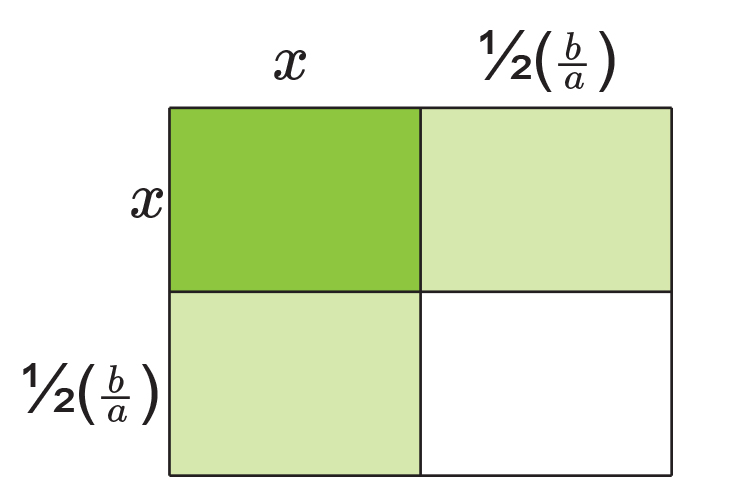
Is the same as
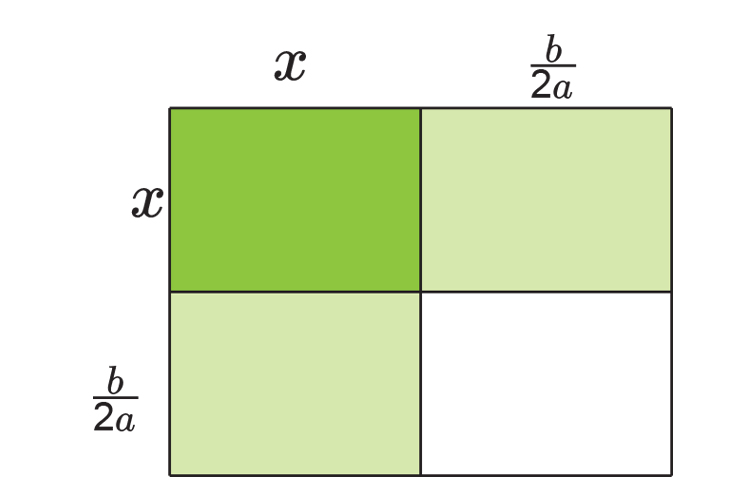
Fill in the table
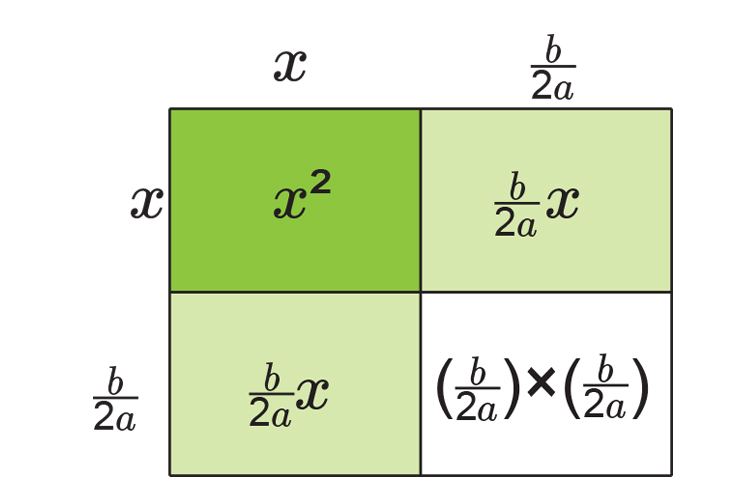
NOTE:
This is the same as `(x+b/(2a))^2`
If you add up each area you get:
`x^2+b/(2a)x+b/(2a)x+(btimesb)/(2atimes2a)`
`x^2+b/ax+b^2/(4a^2)`
We originally had
`x^2+(bx)/a+c/a=0`
We now have
`x^2+b/ax+b^2/(4a^2)`
Original number `-` New number (see completing the square)
`c/a-b^2/(4a^2)`
So `x^2+(bx)/a+c/a=0`
Is the same as:
`(x+b/(2a))^2+c/a-b^2/(4a^2)=0`
`(x+b/(2a))^2=-c/a+b^2/(4a^2)`
`x+b/(2a)=sqrt(-c/a+b^2/(4a^2))`
`x=-b/(2a)+-sqrt(-c/a+b^2/(4a^2))`
This is actually finished but now mathematicians believe that it's better to simplify the formula even more by:
`x=-b/(2a)+-sqrt(-c/a+b^2/(4a^2))`
Multiply the right hand side by `(2a)/(2a)` `(=1)`
`x=(2a)/(2a)times(-b/(2a)+-sqrt(-c/a+b^2/(4a^2)))`
NOTE:
On the next step `(2a)/(2a)=(sqrt((2a)^2))/(2a)` and then
`x=(2a)/(2a)times(-b)/(2a)+-((sqrt((2a)^2))/(2a)timessqrt((-c)/a+b^2/(4a^2)))`
`x=(2a)/(2a)times(-b)/(2a)+-((sqrt((2a)^2)timessqrt((-c)/a))/(2a)+(sqrt((2a)^2)times sqrt(b^2/(4a^2)))/(2a))`
`x=(2a)/(2a)times-b/(2a)+-sqrt((2a)^2times(-c/a)+(2a)^2times(b^2/(4a^2)))/(2a)`
`x=(cancel(2a))/(2a)times(-b/(cancel(2a)))+-sqrt((2a)^2times(-c/a)+(2a)^2times(b^2/(4a^2)))/(2a)`
`x=(-b/(2a))+-(sqrt((2a)times(2cancel(a))times(-(\ c)/cancel(\ a))+(cancel(\ 2a)timescancel(\ 2a)timesb^2)/(cancel(4)timescancel(\ a)timescancel(\ a))))/(2a)`
`x=(-b)/(2a)+-sqrt(-4ac+b^2)/(2a)`
`x=(-b+-sqrt(-4ac+b^2))/(2a)`
`x=(-b+-sqrt(b^2-4ac))/(2a)`
This is now in the format that is recognised and used by mathematicians.




