Using the quadratic formula solver Example 4
Solve `2x^2-7x+6=0`
`x=(-b+-sqrt(b^2-4ac))/(2a)`
Therefore `a=2` , `b=-7` & `c=6`
`x=(-(-7)+-sqrt((-7)^2-4times2times6))/(2times2)`
`x=(7+-sqrt(49-48))/4`
`x=(7+-sqrt1)/4`
`x=(7+-1)/4`
`x=(7+1)/4` or `x=(7-1)/4`
`x=8/4` or `x=6/4`
`x=2` or `x=1\1/2`
Now check your answer
`2x^2-7x+6=0`
If `x=2` `2times2^2-7times2+6=0`
`8-14+6=0` Which is correct
If `x=1\1/2` `2times(3/2)^2-7times(3/2)+6=0`
`2times(9/4)-21/2+6=0`
`18/4-21/2+6=0`
`4\2/4-10\1/2+6=0`
`4\1/2-10\1/2+6=0` Which is correct
Answer:
The roots of `2x^2-7x+6=0` are `x=2` or `x=1\1/2`
Quick stetch example 4
`2x^2-7x+6=0`
| `x=3` | `y=` | `2times3^2-7times3+6=` | `18-21+6` | `=3` | |
| `x=2` | `y=` | `2times2^2-7times2+6=` | `8-14+6` | `=0` | |
| `x=1` | `y=` | `2times1^2-7times1+6=` | `2-7+6` | `=1` | |
| `x=0` | `y=` | `2times0^2-7times0+6=` | `0-0+6` | `=6` |
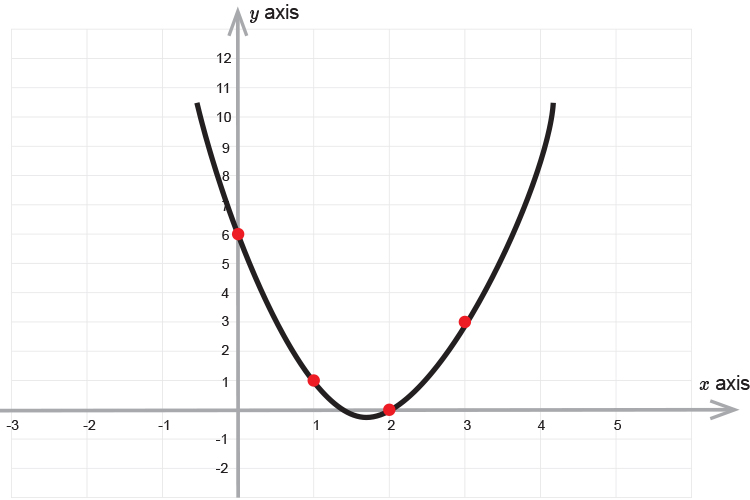
We have found one root as `x=2`