Using the quadratic formula solver Example 3
Solve `2x^2-6x+3=0`
`x=(-b+-sqrt(b^2-4ac))/(2a)`
Therefore `a=2` , `b=-6` & `c=3`
`x=(-(-6)+-sqrt((-6)^2-4times2times3))/(2times2)`
`x=(6+-sqrt(36-24))/4`
`x=(6+-sqrt12)/4`
`x=(6+sqrt12)/4` or `x=(6-sqrt12)/4`
Using a calculator we get
`x=(6+3.464)/4` or `x=(6-3.464)/4`
`x=2.366` or `x=0.634`
Now check the answer
`2x^2-6x+3=0`
If `x=2.366` `2times2.366^2-6times2.366+3=0`
`11.19-14.19+3=0` Which is correct
If `x=0.634` `2times0.634^2-6times0.634+3=0`
`0.804-3.804+3=0` Which is correct
Answer:
The roots of `2x^2-6x+3=0` are `x=2.366` or `x=0.634`
Quick stetch example 3
`2x^2-6x+3=0`
| `x=3` | `y=` | `2times3^2-6times3+3=` | `18-18+3` | `=3` | |
| `x=2` | `y=` | `2times2^2-6times2+3=` | `8-12+3` | `=-1` | |
| `x=1` | `y=` | `2times1^2-6times1+3=` | `2-6+3` | `=-1` | |
| `x=0` | `y=` | `2times0^2-6times0+3=` | `0-0+3` | `=3` |
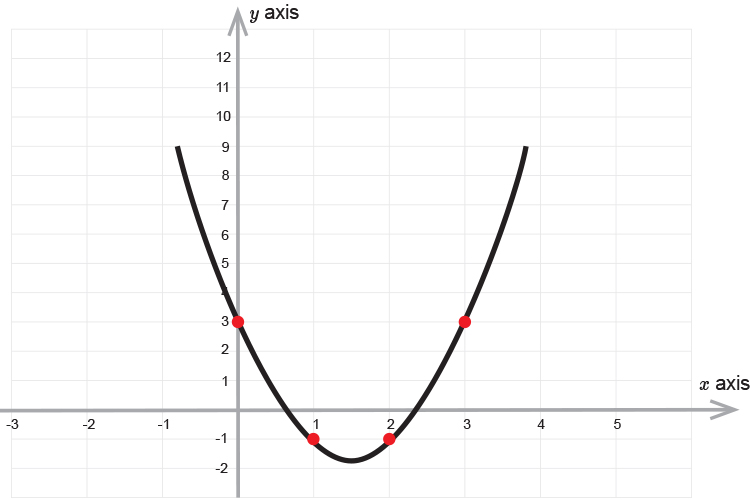
Gives you an idea that the roots are between `0` and `1` and between `2` and `3`




