Ordering fractions by size - Method 2

Putting fractions in smallest to largest can be completed if the bottom numbers (the denominator) are all the same.

 Can't compare unless all the bottom numbers are the same

and to put all the fractions with the same bottom number you must:

1. Find lowest common multiple (LCM) of the bottom numbers.
2. For each fraction find out how many times the bottom number `div` into the LCM.
3. Multiply that fraction top & bottom by that number

 

Example 1

Put the following fractions in order of the smallest to biggest fraction

`8/3`   `5/4`   and  `12/5`

To answer this first find the lowest common multiple (LCM) of the bottom numbers.

 

`60` is the LCM of the bottom number

Now find out how many times the bottom number `div` into the LCM.

`60div3=20`

`60div4=15`

`60div5=12`

Now multiply the fraction top and bottom by that number

`(8times20)/(3times20)=160/60`

`(5times15)/(4times15)=75/60`

`(12times12)/(5times12)=144/60`

So  `8/3=160/60`   and   `5/4=75/60`   and   `12/5=144/60`

Now we can clearly see that the correct order is:

`5/4`  (smallest),   `12/5`  (middle) and  `8/3`  (biggest)

 

Example 2

Put the following fractions in order of the smallest to biggest fraction

`1/2`   `1/3`  `1/4`   `1/6`  and  `1/8`

To answer this first find the lowest common multiple (LCM) of the bottom numbers.

 

`24` is the LCM of the bottom number

Now find out how many times the bottom number `div` into the LCM.

`24div2=12`

`24div3=8`

`24div4=6`

`24div6=4`

`24div8=3`

Now multiply the fraction top and bottom by that number

`(1times12)/(2times12)=12/24`

`(1times8)/(3times8)=8/24`

`(1times6)/(4times6)=6/24`

`(1times4)/(6times4)=4/24`

`(1times3)/(8times3)=3/24`

So  `1/2=12/24`,   `1/3=8/24`,   `1/4=6/24`   `1/6=4/24`   and   `1/8=3/24`

Now we can clearly see that the correct order is:

`1/8`  (smallest) then   `1/6`,   `1/4`,   `1/3` and  `1/2`  (biggest)

 

NOTE:

You should be familiar enough with fractions to realise that the biggest number divided into `1` would obviously be the smallest fraction.

 

Example 3

Which is greater `3/8`  or  `4/9`?

To answer this first find the lowest common multiple (LCM) of the bottom numbers

 

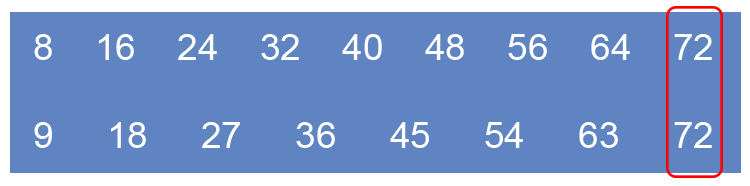
`72` is the LCM of the bottom numbers.

Now find out how many times the bottom number divides into the LCM.

`72div8=9`

`72div9=8`

Now multiply the fraction top and bottom by that number

`(3times9)/(8times9)=27/72`

`(4times8)/(9times8)=32/72`

So `3/8=27/72`   and  `4/9=32/72`

Now we can clearly see that the greater number is `4/9`

 

Example 4

Put the following fractions in order of the smallest to biggest fraction

`2/6`   `1/2`   `7/16`   `3/4`   and  `5/8`

To answer this first find the lowest common multiple (LCM) of the bottom numbers.

 

`48` is the LCM of the bottom number

Now find out how many times the bottom number `div` into the LCM.

`48div2=24`

`48div4=12`

`48div6=8`

`48div8=6`

`48div16=3`

Now multiply the fraction top and bottom by that number

`(1times24)/(2times24)=24/48`

`(3times12)/(4times12)=36/48`

`(2times8)/(6times8)=16/48`

`(5times6)/(8times6)=30/48`

`(7times3)/(16times3)=21/48`

So  `1/2=24/48`,   `3/4=36/48`,   `2/6=16/48`   `5/8=30/48`   and   `7/16=21/48`

Now we can clearly see that the order is:

`2/6`,  `7/16`  `1/2`  `5/8` and  `3/4`

More Info