Inequalities and graphs example 4

Shade the region on the graph that would satisfy all the following inequalities, label this region R.

`x<3` `y>\-2` `y<\x`

Take each inequality separately

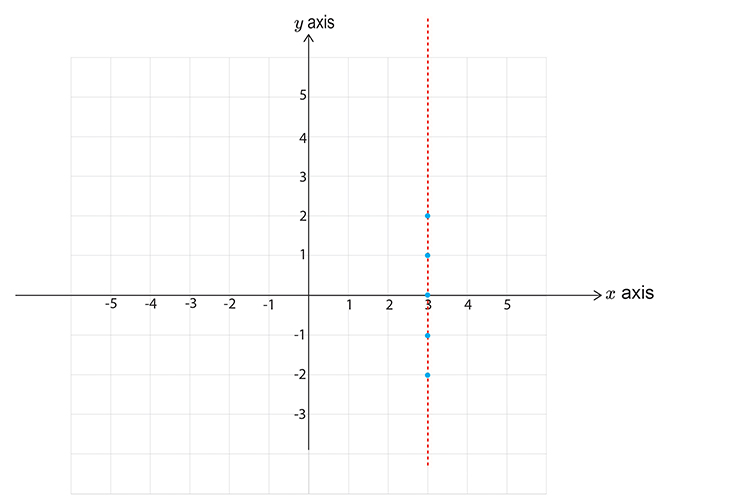
`x<3`

First let’s calculate points on the graph

`y=-2` then `x` is `<3`

`y=-1` then `x` is still `<3`

`y=0` then `x` is still `<3`

`y=1` then `x` is still `<3`

`y=2` then `x` is still `<3`

Now draw a graph and mark the above points.

Don’t forget to use a dotted line.

Draw the dotted line

Now pick a point NOT on the line.

Pick a point not on the line

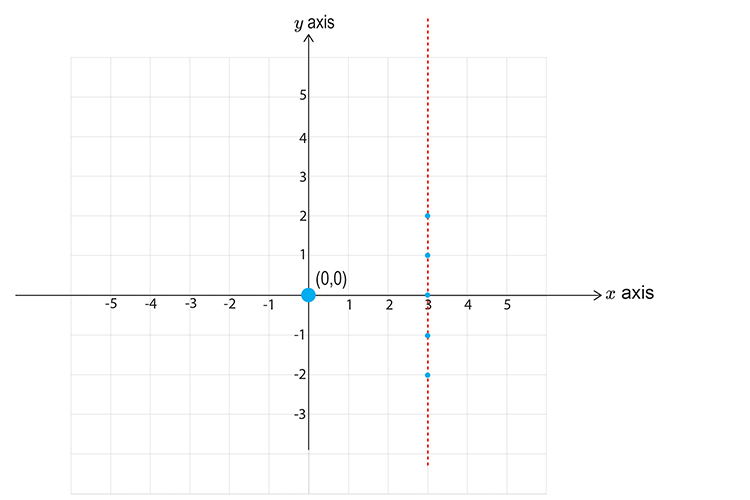
Choose `x=0` `y=0`

`x<3`

`0<3`

This reads zero is less than three.

This DOES satisfy the inequality, SHADE IT.

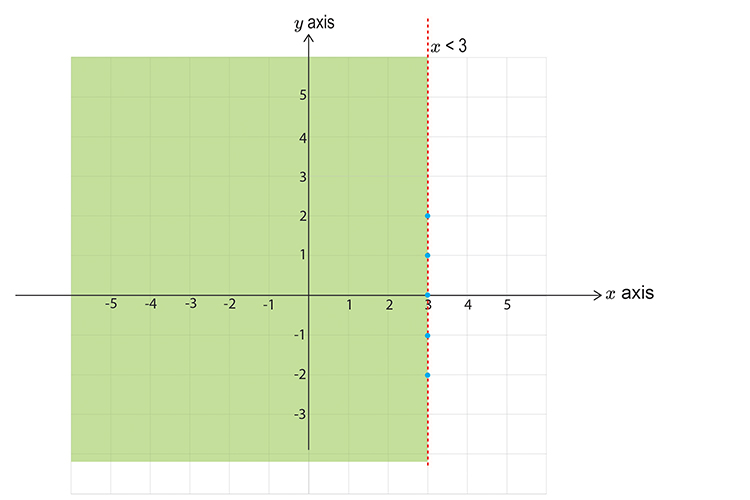
Image of a graph with shaded area

Take the next inequality

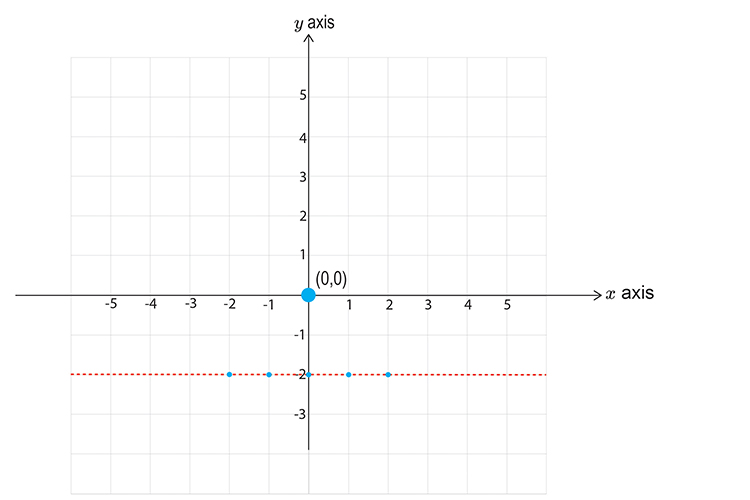
`y>\-2`

First let’s calculate points on the graph

`x=-2` then `y` is `>\-2`

`x=-1` then `y` is `>\-2`

`x=0` then `y` is `>\-2`

`x=1` then `y` is `>\-2`

`x=2` then `y` is `>\-2`

Now draw a graph and mark the above points. Don’t forget to use a DOTTED LINE.

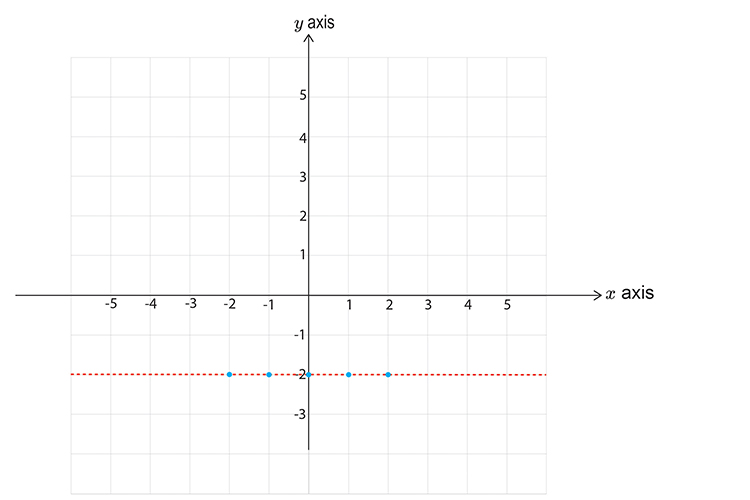
Draw a line with the above points

Now pick a point NOT on the line.

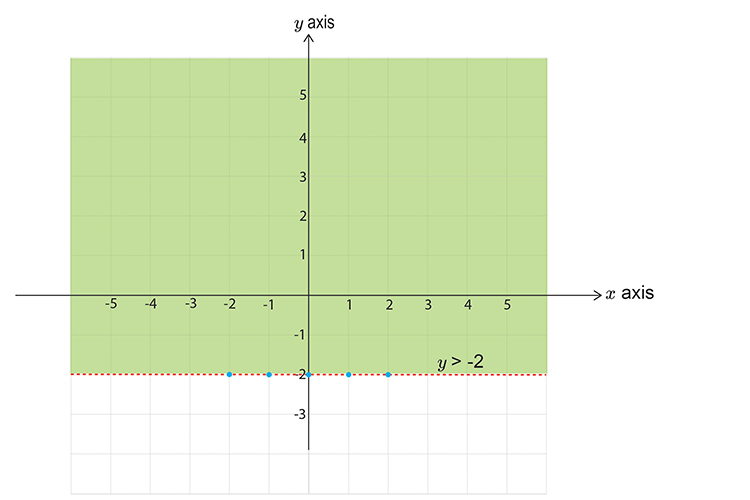
Pick a point not on the line

Choose `x=0` `y=0`

`y>\-2`

`0>\-2`

This reads zero is greater than minus two.

This DOES satisfy the inequality, SHADE IT.

Shade it

Take the final inequality

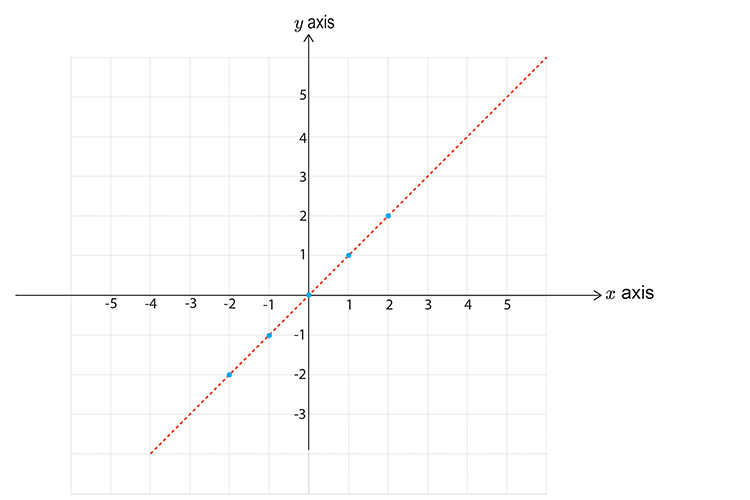
`y<x`

First let’s calculate points on the graph

`x=-2` then `y <-2`

`x=-1` then `y <-1`

`x=0` then `y <0`

`x=1` then `y <1`

`x=2` then `y <2`

Now draw a graph and mark the above points. Don’t forget to draw a DOTTED line.

Draw a diagonal dotted line

Now pick a point NOT on the line.

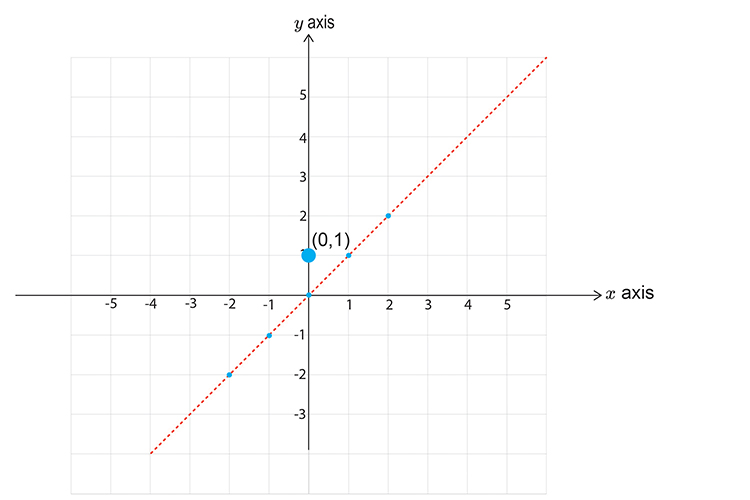
Pick your point

Choose `x=0` `y=0`

`y<\x`

`1<\0`

This reads one is less than zero, which is obviously wrong and therefore this does NOT satisfy the inequality, SHADE THE OTHER HALF.

If it is not satisfied shade the other half

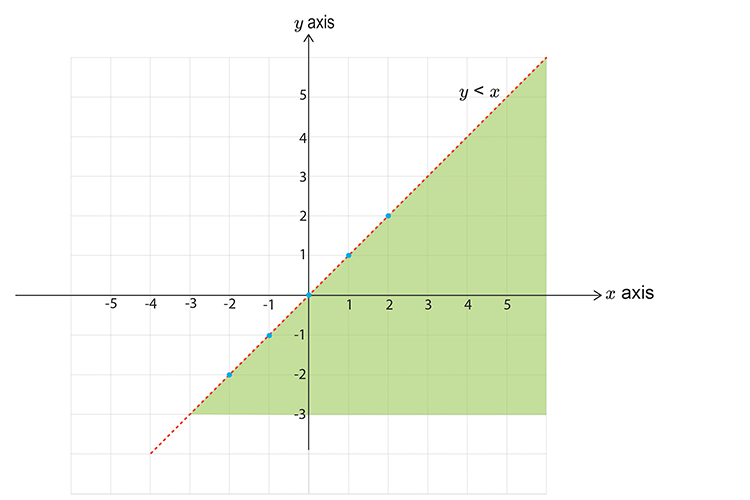
Now plot all three graphs.

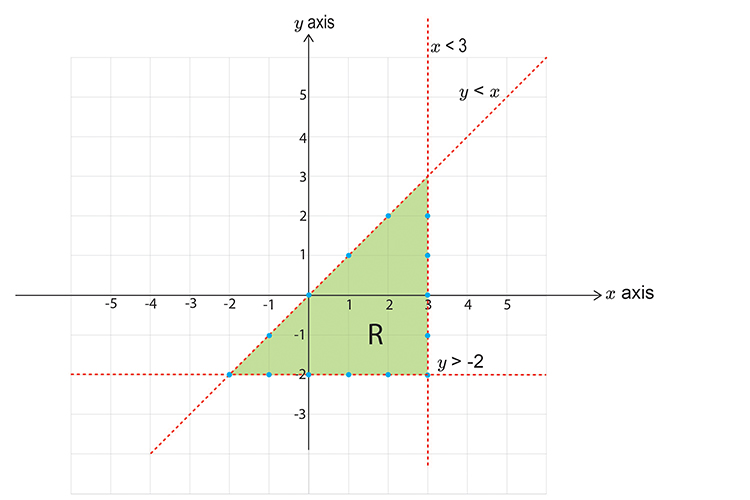
Now plot all 3 lines the triangle made satisfies all the inequalities

R satisfies all the inequalities.