Inequalities and graphs example 5

On a graph mark with a cross (X) six points that satisfy all 3 of the following inequalities

`-2<\x<=1` `y>\-2` `y<\x+1`

Where `y` and `x` are integers.

Take each inequality separately

`-2<\x<=1`

Split this into

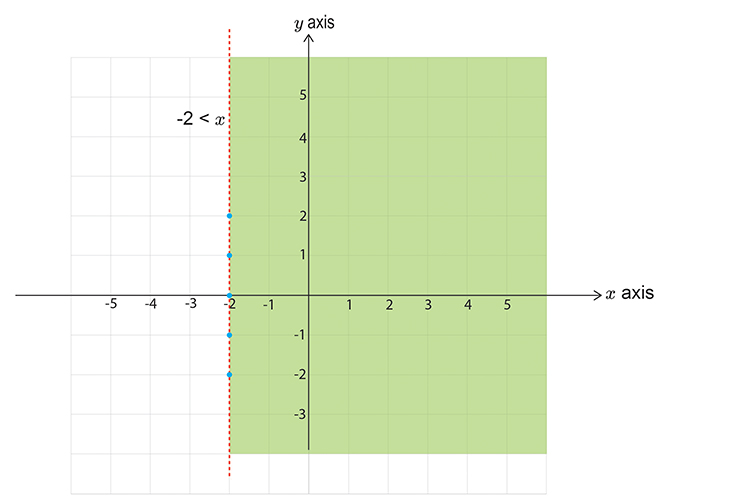
`-2<\x`

`x<=1`

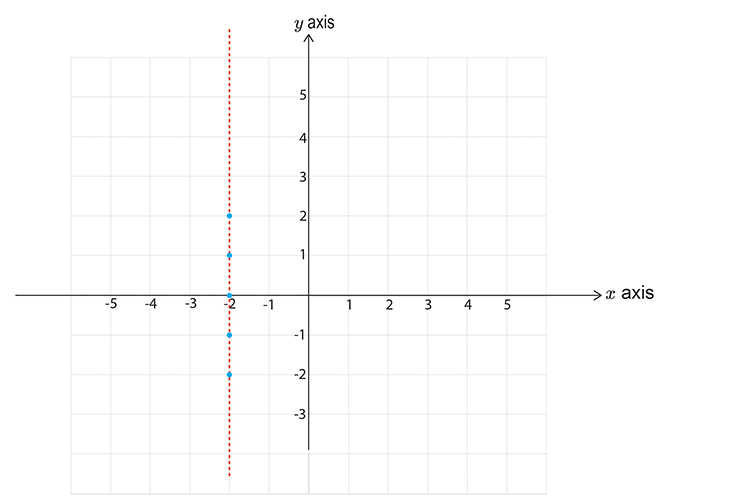
i. `-2<x`

First let's calculate some points on the graph

`y=-2` `x` is greater than -2

`y=-1` `x` is still greater than -2

`y=0` `x` is still greater than -2

`y=1` `x` is still greater than -2

`y=2` `x` is still greater than -2

Now draw a graph and mark these points.

Don’t forget to use a DOTTED line.

Draw the vertical dotted line

Now pick a point not on the line.

Pick a point on the graph, not on the line

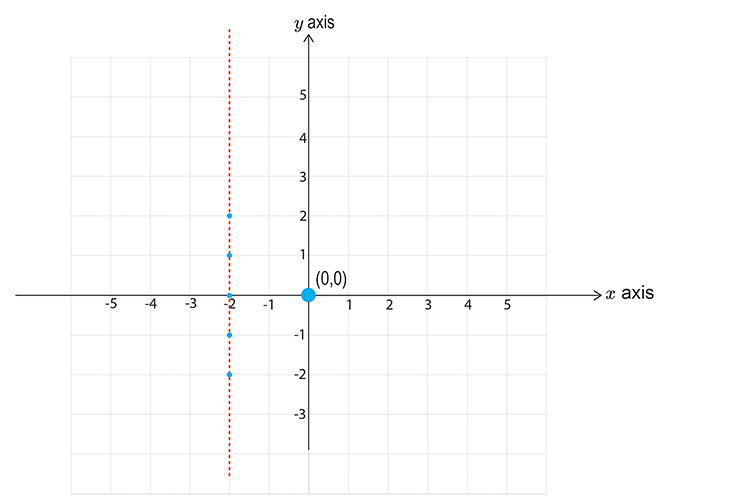
Choose `x=0` `y=0`

`-2<\x`

`-2<\0`

This reads minus two is less than zero, which is correct.

So this DOES satisfy the inequality, SHADE IT.

Shade as applicable

Now part two

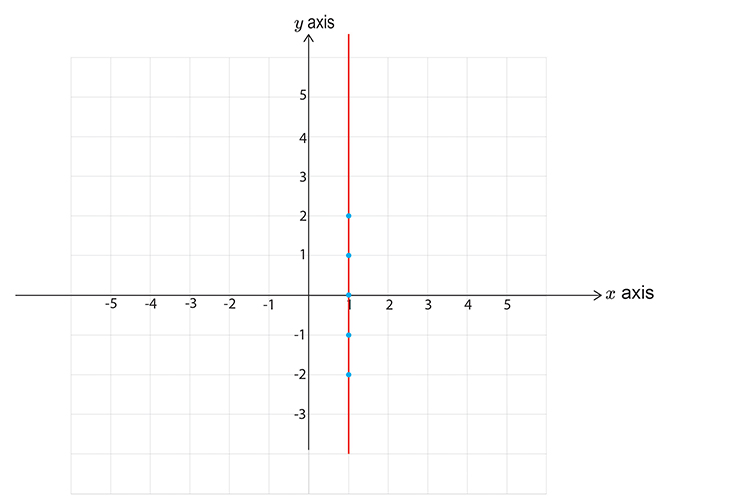
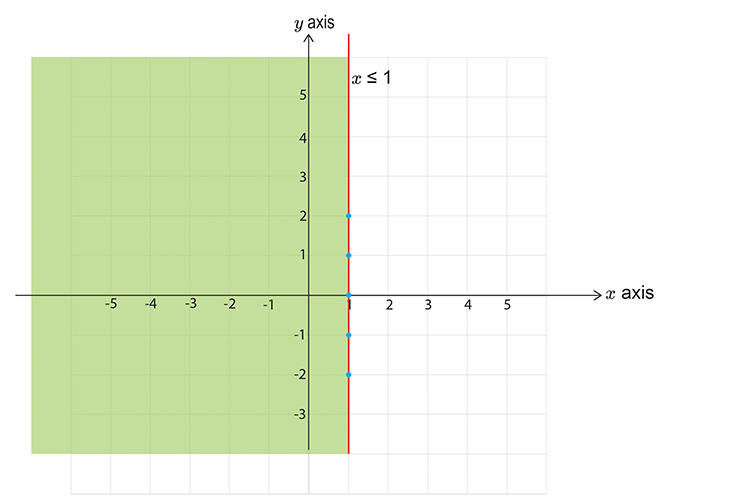
ii. `x<=\1`

First lets calculate points on the graph

`y=-2` `x` is less than or equal to 1

`y=-1` `x` is still less than or equal to 1

`y=0` `x` is still less than or equal to 1

`y=1` `x` is still less than or equal to 1

`y=2` `x` is still less than or equal to 1

Now draw a graph and mark the above points.

Don’t forget to use a SOLID LINE.

Draw the next solid vertical line

Now pick a point NOT on the line.

Pick a point not on the line

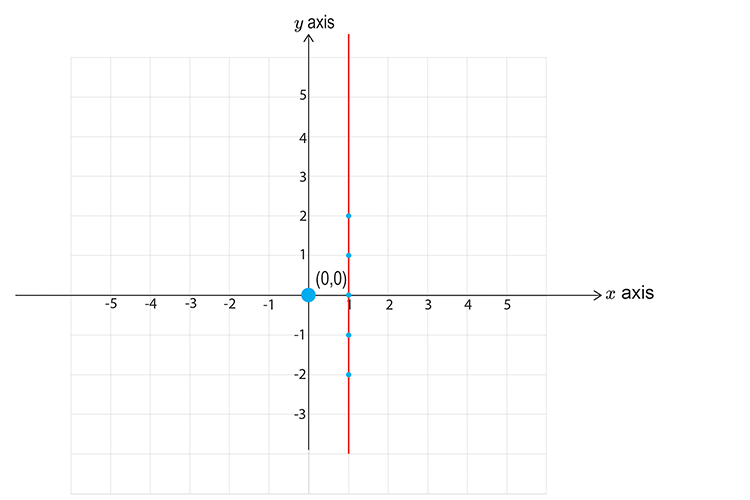
Lets choose `x=0` `y=0`

`x<=\1`

`0<=\1`

This reads zero is less than or equal to one, which is correct.

So this DOES satisfy the inequality, SHADE IT.

Shade it if its satisfied

Now choose the next inequality

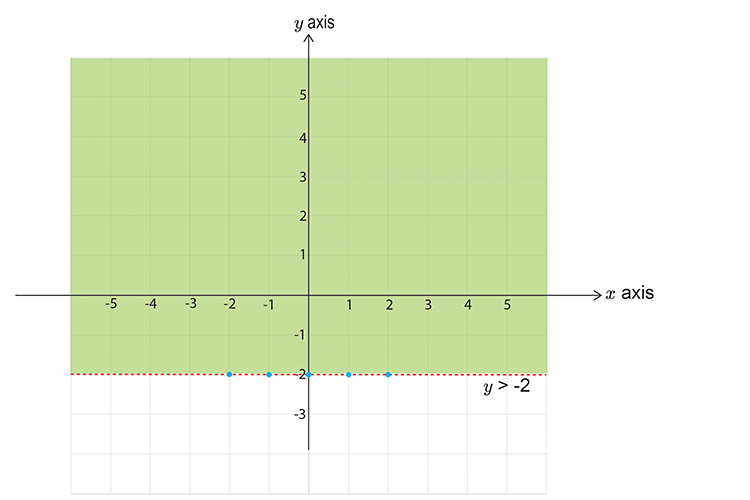
`y>\-2`

First calculate points on the graph.

`x=-2` `y` is greater than -2

`x=-1` `y` is still greater than -2

`x=0` `y` is still greater than -2

`x=1` `y` is still greater than -2

`x=2` `y` is still greater than -2

Now draw a graph and mark the above points.

Don’t forget to use a DOTTED LINE.

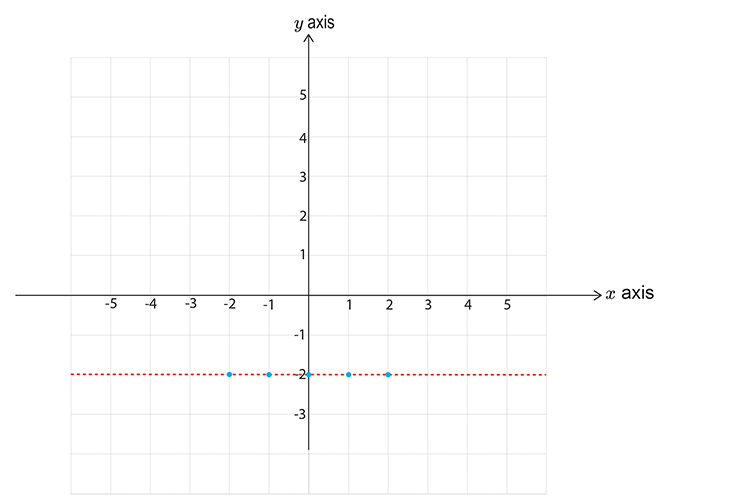
Draw the next dotted horizontal line

Now pick a point NOT on the line.

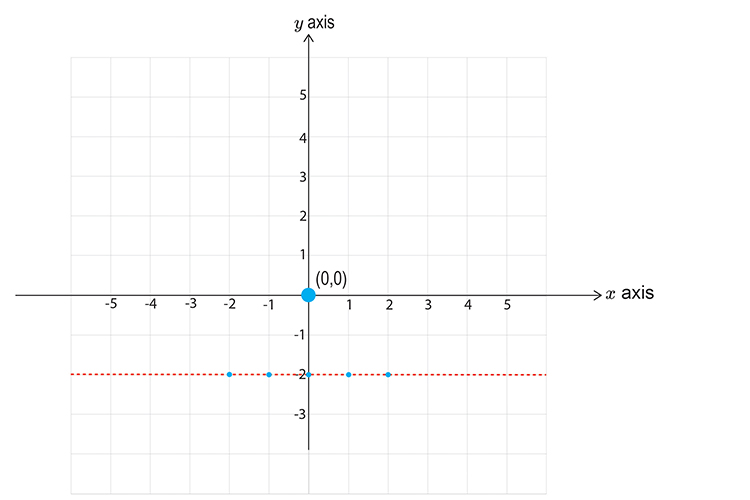
Find the random point on the graph

Choose `x=0` `y=0`

`y>\-2`

`0>\-2`

This reads zero is greater than minus two, which is correct.

So this DOES satisfy the inequality, SHADE IT.

Shade it if its satisfied

Now for the final inequality

`y<\x\+1`

First let’s calculate points on the graph

`x=-2` `y<-2+1=-1`

`x=-1` `y<-1+1=0`

`x=0` `y<0+1=1`

`x=1` `y<1+1=2`

`x=2` `y<2+1=3`

Now draw a graph and mark the above points.

Don’t forget to use a DOTTED line.

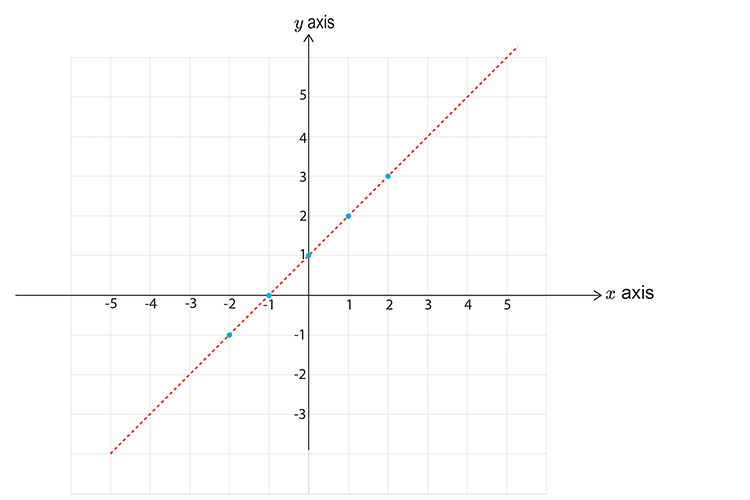
Draw the dotted diagonal line

Now pick a point NOT on the line.

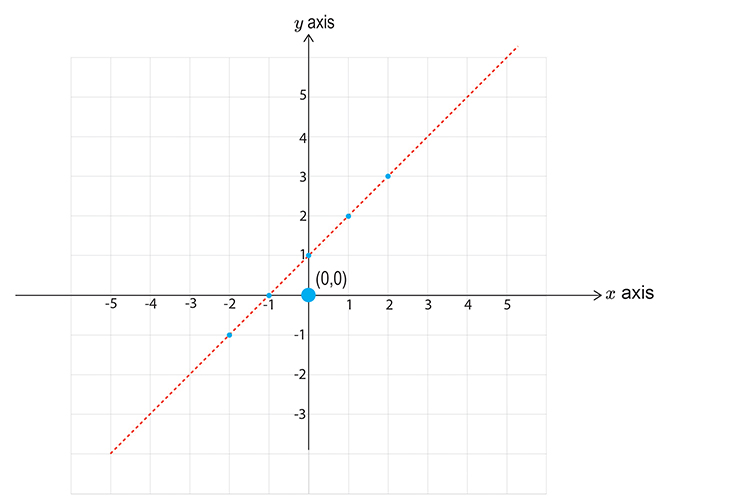
Plot a random position on the graph

Lets choose `x=0` `y=0`

`y<\x+1`

`0<\0+1`

`0<\1`

This reads zero is less than one, which is correct.

So this DOES satisfy the inequality so SHADE IT.

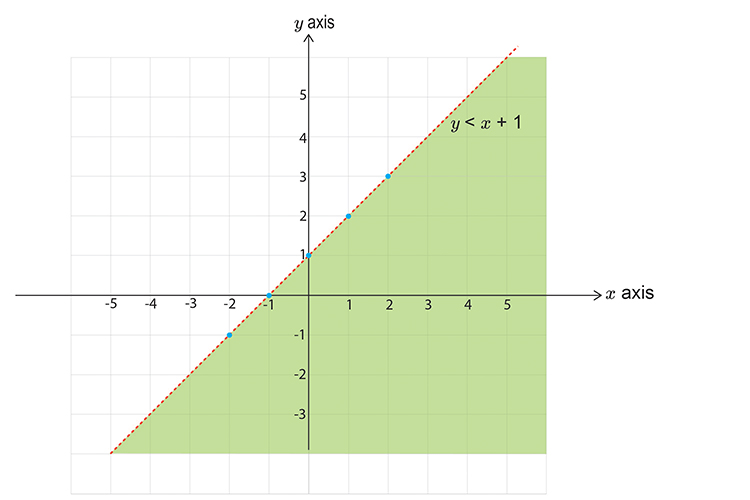
Shade if necessary

NOW PUT ALL THE GRAPHS TOGETHER. And shade the area that would be covered by all the shaded regions.

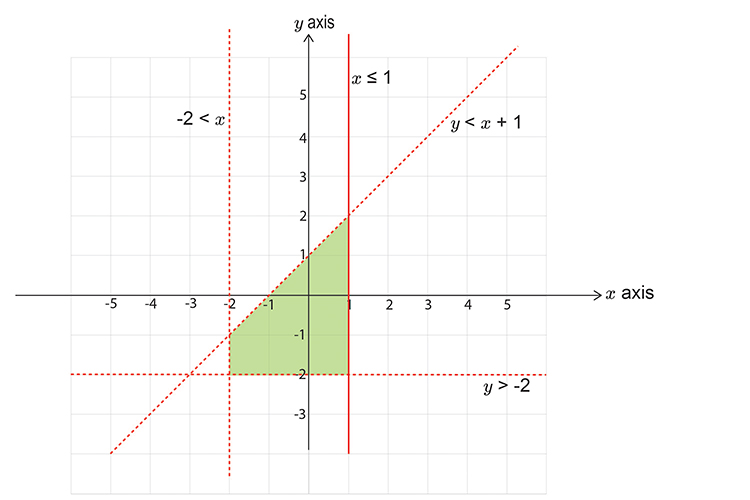
Plot all the graphs and shade all the areas that would have been shaded

Now mark with a cross (x), six points that satisfy all 3 of the inequalities (that are also integers).

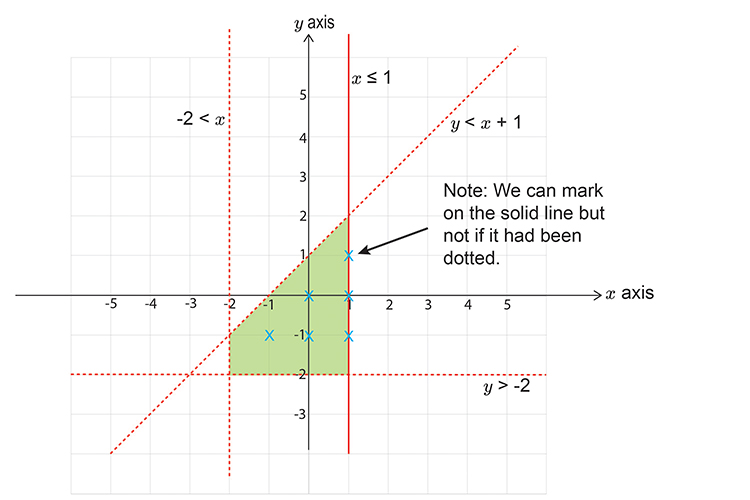
Only mark on solid lines not on dotted lines

NOTE:

These are the only six points we could have chosen.