Formula for `n^(th)` term of a sequence - consistent difference between differences
The formula is `an^2+bn+c` and this is explained by the following:
The following pattern is known as a quadratic.
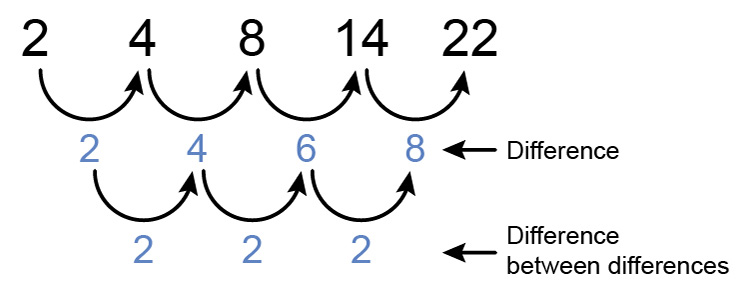
When we know we are dealing with a sequence that is a quadratic (where the difference between differences are consistent) we must remember the facts about quadratics.

See mammoth memory quadratics to understand the above picture.
(A quadratic is an `x^2` term `=ax^2+bx+c`)
A quadratic is
`ax^2+bx+c`
but here the `x` is replaced by the letter `n` denoting the number in a sequence.
The quadratic becomes
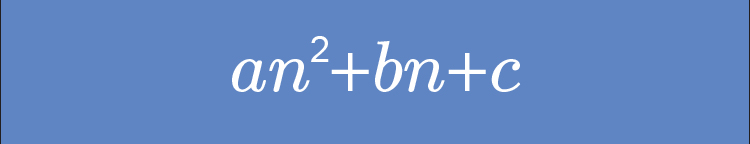
and this is all you need to remember because
The first term is
1st term (where `n=1`) `=atimes1^2+btimes1+c`
is the same as
1st term`=a+b+c`
The second term is
2nd term `(n=2)=atimes2^2+btimes2+c`
is the same as
2nd term `=4a+2b+c`
The third term is
3rd term `(n=3)=atimes3^2+btimes3+c`
is the same as
3rd term `=9a+3b+c`
Summary
So we know
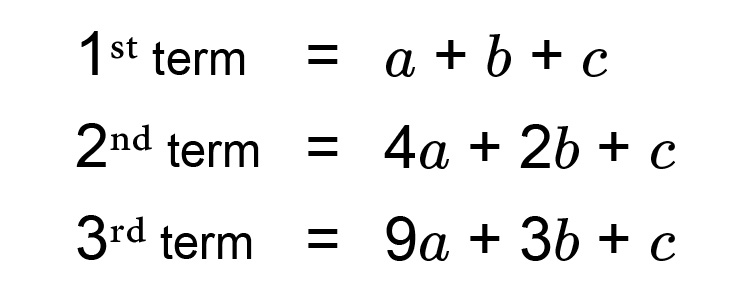
So for any quadratic sequence (consistent difference between differences) we can use this information to work out ANY `n^(th)` term formula.




