Triangles and the `n^(th)` term

`1`   `3`   `6`   `10`   `15`

You can recognise a triangular sequence by picturing it as follows:

 

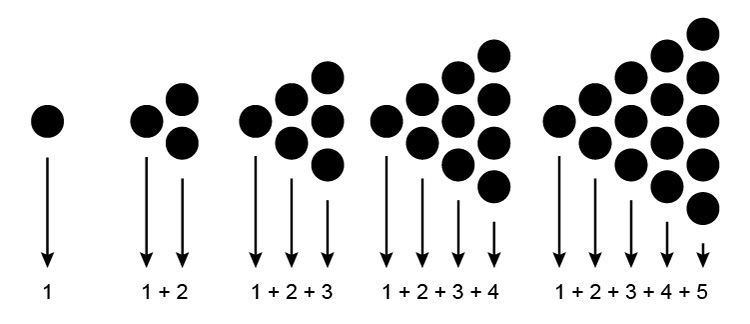
We can see a pattern emerge

`1^(st)`	term `=1`	`=1`
`2^(nd)`	term `=1+2`	`=3`
`3^(rd)`	term `=1+2+3`	`=6`
`4^(th)`	term `=1+2+3+4`	`=10`
`5^(th)`	term `=1+2+3+4+5`	`=15`

This also gives us a clue as to how we find the `n^(th)`  term of any triangular sequence (But note the following only applies when the sequence starts at the number 1).

 

At first, just take one large even set of `n^(th)`  terms

Try `12^(th)` term

The `12^(th)` term would be

`1+2+3+4+5+6+7+8+9+10+11+12=78`

But a mathematician found that if you started by adding the `1^(st)` and last term together and then continue this arrangement then a pattern emerges.

i.e.

 

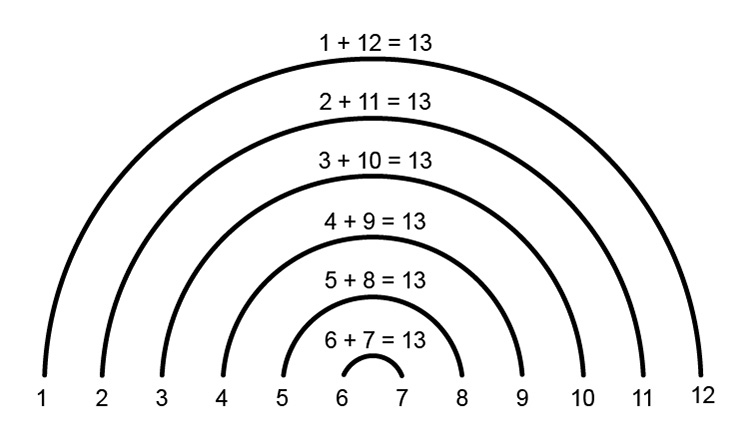
`12^(th)` term`=`	`1+12`	`=13`
	`2+11`	`=13`
	`3+10`	`=13`
	`4+9`	`=13`
	`5+3`	`=13`
	`6+7`	`=13`
		`6times13`	`=78`

So the pattern is `13` and the multiple is `6`.

This works for any even numbered triangular number.

Try `16^(th)` term

`16^(th)`  term`=`	`1+16`	`=17`
	`2+15`	`=17`
	`3+14`	`=17`
	`4+13`	`=17`
	`5+12`	`=17`
	`6+11`	`=17`
	`7+10`	`=17`
	`8+9`	`=17`
		`8times17`	`=136`

So the pattern is `17` and the multiple is `8`.

Now we can form a formula for this

 

Stage 1 find the pattern number

`12^(th)` term `=(12+1)=13`

`16^(th)` term `=(16+1)=17`

So the pattern number `=(n^(th)\ \n\u\m\b\e\r+1)`

 

Stage 2

And the amount of times we repeat this pattern number (the multiple)

`12^(th)` term `=(12)/2=6`

`16^(th)` term `=(16)/2=8`

So the multiple `=(n^(th)\ term)/2`

 

Put stage 1 and stage 2 together we get:

`(n^(th)\ term+1)times(n^(th)\ term)/2`

So the `n^(th)\ term=(n+1)timesn/2`

 

And amazingly this also works for odd triangular numbers too.

 

Example 1

What is the `9^(th)` term of the triangular sequence

Either draw it

 

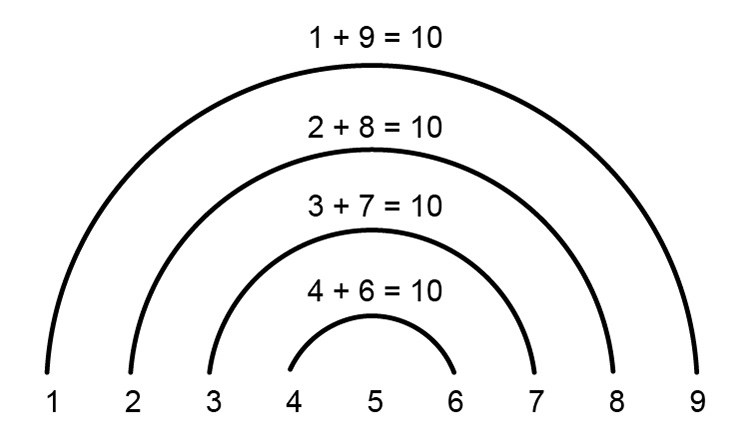
`9^(th)` term`=`	`1+9`	`=10`
	`2+8`	`=10`
	`3+7`	`=10`
	`4+6`	`=10`
		`4times10`	`+5=45`

NOTE:

We add `5` because that is the number missed in the series of semi-circles above.

 

or using the formula

`(n+1)timesn/2`

`9^(th)`  term	`=(9+1)times9/2`
	`=(10times9)/2`
	`=5times9`
	`=45`

 

 

Example 2

What is the `11^(th)` term of the triangular sequence

Either draw it

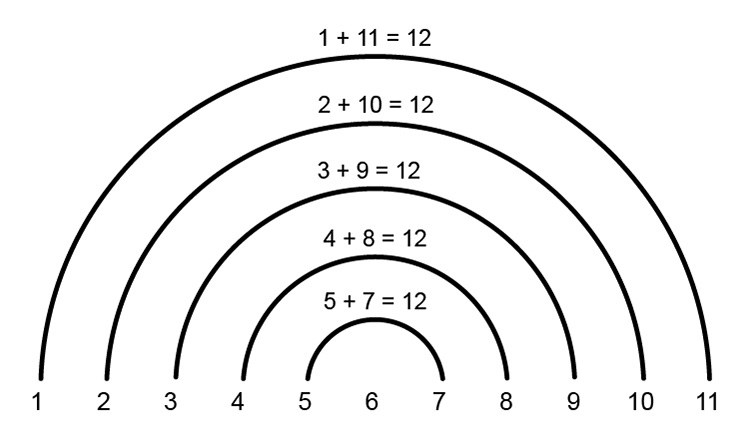
`11^(th)` term`=`	`1+11`	`=12`
	`2+10`	`=12`
	`3+9`	`=12`
	`4+8`	`=12`
	`5+7`	`=12`
		`5times12`	`+6=66`

 NOTE:

We add `6` because that is the number missed in the series of semi-circles above.

 

or using the formula

`(n+1)timesn/2`

`11^(th)`  term	`=(11+1)times11/2`
	`=(12times11)/2`
	`=6times11`
	`=66`

 

 

Example 3

What is the `27^(th)` term of the triangular sequence

We are not going to draw this out but we can just rely on the formula.

`(n+1)timesn/2`

`27^(th)`  term	`=(27+1)times27/2`
	`=(28times27)/2`
	`=14times27`
	`=378`

 

 

Example 4

What is the `28^(th)` term of the triangular sequence

Again we are not going to draw this out but the formula gives:

`(n+1)timesn/2`

`28^(th)`  term	`=(28+1)times28/2`
	`=(29times28)/2`
	`=29times14`
	`=406`

 

(As a point of interest comparing example 3 and the answer 378 and here 406 the difference is 28 which would be correct.)

More Info