Formula for `n^(th)` term of a sequence - consistent difference

In order to predict the `n^(th)` term of a sequenece you will need to create a formula.

For sequence patterns of consistent differences finding the `n^(th)` term of a linear sequence (an addition or subtraction sequence) is worked out by.

You can also extend sequences for the consistent difference sequences

or in more detail

Nth term in text detail

Summary

Formula for `n^(th)` term `=` Difference `timesn+(`first term`-`difference`)`

Example 1

Even numbers

What is the formula for the `n^(th)` term for the following sequence, and what is the `11^(th)` term?

`2`, `4`, `6`, `8`, `10`, `12`

To tackle this always find the sequence pattern.

First, see if there is a consistent difference between each number.

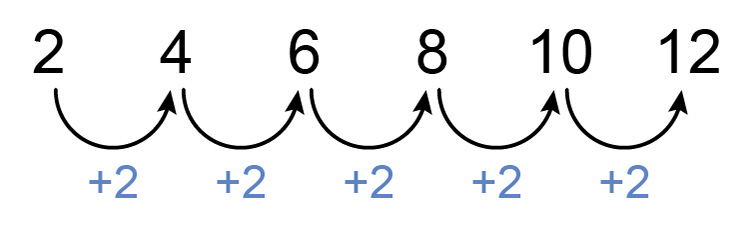
Extend this sequence to its 11th term, the difference will still be 2

Yes and that number is `2`

Now to find the formula:

i. Find the difference and multiply by `n` `=2n`

The difference is `2`

Which we now multiply by `n`

Therefore this equals `2n`

ii. Find the value between the first term and the consistent difference.

First term	`=`	`2`
Consistent difference	`=`	`2`
Take them away	`=`	`0`

So the value between the first term and the consistent difference `=0`

iii. Adding the two together we get the formula for this sequence as:

Formula for `n^(th)` term `=2n+0`

Answer: The formula for the `n^(th)` term `=2n`

NOTE:

This formula is well known as the sequence progression for even numbers.

Always check the formula is correct.

Try different values of `n` in the formula `2n`

If `n=1` therefore term `=2times1=2`

If `n=2` therefore term `=2times2=4`

If `n=3` therefore term `=2times3=6`

This is correct

Now we have the correct formula we can work out the other terms.

The `11^(th)` term would be:

If `n=11` then `2n=2times11=22`

Answer: The `11^(th)` term `=22`

Example 2

Odd numbers

What is the formula for the `n^(th)` term for the following sequence, and what is the `14^(th)` term.

`1`, `3`, `5`, `7`, `9`, `11`

To tackle this always find the sequence pattern.

First, see if there is a consistent difference between each number.

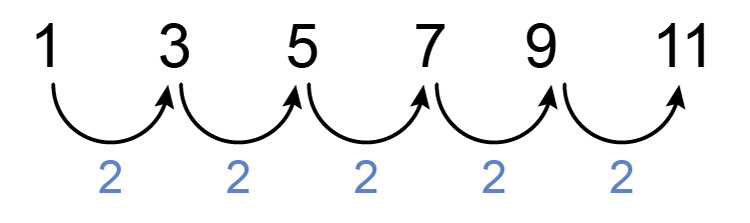
Extend this sequence to its 14th term, the difference will still be 2

Yes and that number is `2`

Now to find the formula:

i. Find the difference and multiply by `n` `=2n`

The difference is `2`

Which we now multiply by `n`

Therefore this equals `2n`

ii. Find the value between the first term and the consistent difference.

First term	`=`	`1`
Consistent difference	`=`	`2`
Take them away	`=`	`-1`

So the value between the first term and the consistent difference `=-1`

iii. Adding the two together we get the formula for this sequence as:

Formula for `n^(th)` term `=2n-1`

Answer: The formula for the `n^(th)` term `=2n-1`

NOTE:

This formula is well known as the sequence progression for odd numbers.

Always check the formula is correct.

Try different values of `n` in the formula `2n-1`

If `n=1` therefore term `=2times1-1=1`

If `n=2` therefore term `=2times2-1=3`

If `n=3` therefore term `=2times3-1=5`

If `n=4` therefore term `=2times4-1=7`

This is correct

Now we have the correct formula we can work out other terms.

The `14^(th)` term would be:

If `n=14` then `2n-1=2times14-1=27`

Answer: The `14^(th)` term `=27`

Example 3

What is the formula for the `n^(th)` term for the following sequence, and what is the `55^(th)` term.

`6`, `8`, `10`, `12`, `14`

To tackle this always find the sequence pattern.

First, see if there is a consistent difference between each number.

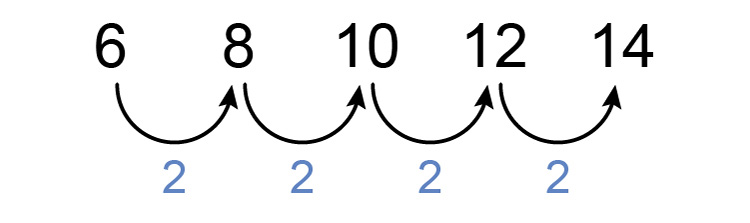
Extend this sequence to its 55th term, the difference will still be 2

Yes and that number is `2`

Now to find the formula:

i. Find the difference and multiply by `n` `=2n`

The difference is `2`

Which we now multiply by `n`

Therefore this equals `2n`

ii. Find the value between the first term and the consistent difference.

First term	`=`	`6`
Consistent difference	`=`	`2`
Take them away	`=`	`4`

So the value between the first term and the consistent difference `=4`

iii. Adding the two together we get the formula for this sequence as:

Formula for `n^(th)` term `=2n+4`

Answer: The formula for the `n^(th)` term `=2n+4`

Always check the formula is correct.

Try different values of `n` in the formula `2n+4`

If `n=1` therefore term `=2times1+4=6`

If `n=2` therefore term `=2times2+4=8`

If `n=3` therefore term `=2times3+4=10`

This is correct

Now we have the correct formula we can work out the other terms.

The `55^(th)` term would be:

If `n=55` then `2n+4=2times55+4=114`

Answer: The `55^(th)` term `=114`

Example 4

What is the formula for the `n^(th)` term for the following sequence, and what is the `7^(th)` term.

`12`, `10`, `8`, `6`, `4`

To tackle this always find the sequence pattern.

First, see if there is a consistent difference between each number.

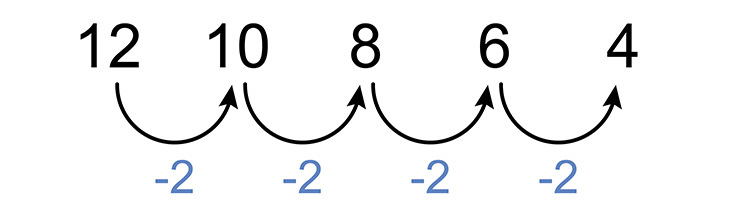
Extend this sequence to its 7th term, the difference will still be minus 2

Yes and that number is `-2`

Now to find the formula:

i. Find the difference and multiply by `n` `=-2n`

The difference is `-2`

Which we now multiply by `n`

Therefore this equals `-2n`

ii. Find the value between the first term and the consistent difference.

First term	`=`	`12`
Consistent difference	`=`	`-2`
Take them away	`=`	`14`

So the value between the first term and the consistent difference `=14`

iii. Adding the two together we get the formula for this sequence as:

Formula for `n^(th)` term `=-2n+14`

Answer: The formula for the `n^(th)` term `=-2n+14`

Always check the formula is correct.

Try different values of `n` in the formula `-2n+14`

If `n=1` therefore term `=-2times1+14=12`

If `n=2` therefore term `=-2times2+14=10`

If `n=3` therefore term `=-2times3+14=8`

This is correct

Now we have the correct formula we can work out other terms.

The `7^(th)` term would be:

If `n=7` then `-2n+14=-2times7+14=0`

Answer: The `7^(th)` term `=0`