Using the quadratic formula to find `n^(th)` term of a sequence - consistent difference between differences

Method 1

This is the easiest to remember but takes the most time to work out an answer.

We know (from the last section) that:

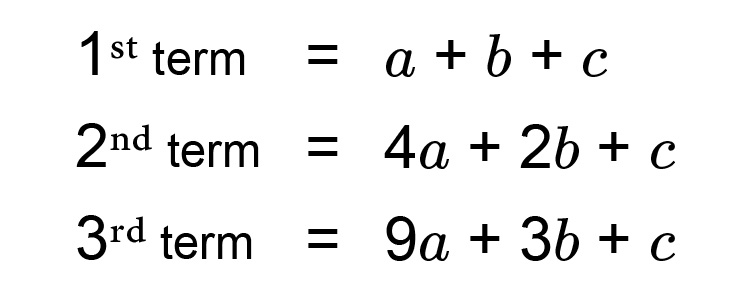
Summary of 1st, 2nd and 3rd quadratic terms

Once you have found `a,b,\ &\ c` you can slot these figures in the following formula.

`an^2+bn+c`

Example 1

Square numbers

We know the following sequence is a quadratic sequence but what is the formula for the `n^(th)` term and what is the `14^(th)` term?

What is the 14th term of this sequence using method 1

The 1st term `=a+b+c`

so `1=a+b+c`

The 2nd term `=4a+2b+c`

so `4=4a+2b+c`

The 3rd term `=9a+3b+c`

so `9=9a+3b+c`

Now you have 3 simultaneous equations.

`1=a+b+c` .................... (1)

`4=4a+2b+c` ................ (2)

`9=9a+3b+c` ................ (3)

Now solve for one letter at a time

`1=a+b+c`

therefore `c=1-a-b`

Substitute this into equations (2) and (3).

`4=4a+2b+1-a-b`

`9=9a+3b+1-a-b`

These two simultaneous equations become

`4-1=4a-a+2b-b`

and `9-1=9a-a+3b-b`

Which simplify to

`3=3a+b` ........... (i)

and `8=8a+2b` .......... (ii)

Now we can solve these two simultaneous equations

`3=3a+b`

is the same as `b=3-3a`

substitute this into (ii)

`8=8a+2(3-3a)`

which is `8=8a+6-6a`

which is `8-6=8a-6a`

becomes `2=2a`

therefore `a=1`

Sustitute `a=1` into (i)

and `3=3a+b`

becomes `3=3times1+b`

`b=3-3=0`

Now substitute `a=1` and `b=0` into equation (1)

`1=a+b+c`

`1=1+0+c`

`c=1-1=0`

Summary `a=1` `b=0` and `c=0`

therefore the formula for the `n^(th)` term in this sequence is

`an^2+bn+c`

or `1n^2+0n+0`

which is `n^2`

Now we need to check the formula is correct.

Try different values of `n` in the formula `n^2`

If `n=1` term `=1^2=1`

If `n=2` term `=2^2=4`

If `n=3` term `=3^2=9`

If `n=4` term `=4^2=16`

This is correct

The 14th term would be

If `n=14` then `n^2=14^2=196`

The 14th term `=196`

Example 2

We know the following sequence is a quadratic sequence but what is the formula of the `n^(th)` term and what is the 16th term?

What is the 16th term of this sequence using method 1

The 1st term `=a+b+c`

so `2=a+b+c`

The 2nd term `=4a+2b+c`

so `4=4a+2b+c`

The 3rd term `=9a+3b+c`

so `8=9a+3b+c`

Now you have 3 simultaneous equations.

`2=a+b+c` .................... (1)

`4=4a+2b+c` ................ (2)

`8=9a+3b+c` ................ (3)

Now solve for one letter at a time

`2=a+b+c`

therefore `c=2-a-b`

Substitute this into equations (2) and (3).

`4=4a+2b+(2-a-b)`

`8=9a+3b+(2-a-b)`

These two simultaneous equations become

`4-2=4a-a+2b-b`

and `8-2=9a-a+3b-b`

Which simplify to

`2=3a+b` ............ (i)

and `6=8a+2b` .......... (ii)

Now we can solve these two simultaneous equations

`2=3a+b`

is the same as `b=2-3a`

substitute this into (ii)

`6=8a+2(2-3a)`

which is `6=8a+4-6a`

which is `6-4=8a-6a`

becomes `2=2a`

therefore `a=1`

Sustitute `a=1` into (i)

and `2=3a+b`

becomes `2=3times1+b`

`b=2-3=-1`

Now substitute `a=1` and `b=-1` into equation 1

`2=a+b+c`

`2=1-1+c`

`c=2`

Summary `a=1` `b=-1` and `c=2`

therefore the formula for the `n^(th)` term in this sequence is

`an^2+bn+c`

or `1n^2+(-1)n+2`

which is `n^2-n+2`

Now we need to check the formula is correct.

Try different values of `n` in the formula `n^2-n+2`

If `n=1` term `=1^2-1+2=2`

If `n=2` term `=2^2-2+2=4-2+2=4`

If `n=3` term `=3^2-3+2=9-3+2=8`

If `n=4` term `=4^2-4+2=16-4+2=14`

This is correct

The 16th term would be

If `n=16` then `n^2-n+2=16^2-16+2=256-16+2=242`

The 16th term `=242`

Example 3

We know the following sequence is a quadratic sequence but what is the formula of the `n^(th)` term and what is the 12th term?

What is the 12th term of this sequence using method 1

The 1st term `=a+b+c`

so `4=a+b+c`

The 2nd term `=4a+2b+c`

so `7=4a+2b+c`

The 3rd term `=9a+3b+c`

so `12=9a+3b+c`

Now you have 3 simultaneous equations.

`4=a+b+c` ..................... (1)

`7=4a+2b+c` ................ (2)

`12=9a+3b+c` ................ (3)

Now solve for one letter at a time

`4=a+b+c`

therefore `c=4-a-b`

Substitute this into equations (2) and (3).

`7=4a+2b+(4-a-b)`

`12=9a+3b+(4-a-b)`

These two simultaneous equations become

`7-4=4a-a+2b-b`

and `12-4=9a-a+3b-b`

Which simplify to

`3=3a+b` ........... (i)

and `8=8a+2b` .......... (ii)

Now we can solve these two simultaneous equations

`3=3a+b`

is the same as `b=3-3a`

substitute this into (ii)

`8=8a+2(3-3a)`

which is `8=8a+6-6a`

which is `8-6=8a-6a`

becomes `2=2a`

therefore `a=2/2=1`

Sustitute `a=1` into (i)

and `3=3a+b`

becomes `3=3times1+b`

`b=3-3=0`

Now substitute `a=1` and `b=0` into equation (1)

`4=a+b+c`

`4=1+0+c`

`c=4-1`

`c=3`

Summary `a=1` `b=0` and `c=3`

therefore the formula for the `n^(th)` term in this sequence is

`an^2+bn+c`

or `1n^2+0n+3`

which is `n^2+3`

Now we need to check the formula is correct.

Try different values of `n` in the formula `n^2+3`

If `n=1` term `=1^2+3=1+3=4`

If `n=2` term `=2^2+3=4+3=7`

If `n=3` term `=3^2+3=9+3=12`

If `n=4` term `=4^2+3=16+3=19`

This is correct

The 12th term would be

If `n=12` then `n^2+3=12^2+3`

`=144+3`

`=147`

The 12th term `=147`

Example 4

We know the following sequence is a quadratic sequence but what is the formula of the `n^(th)` term and what is the 11th term?

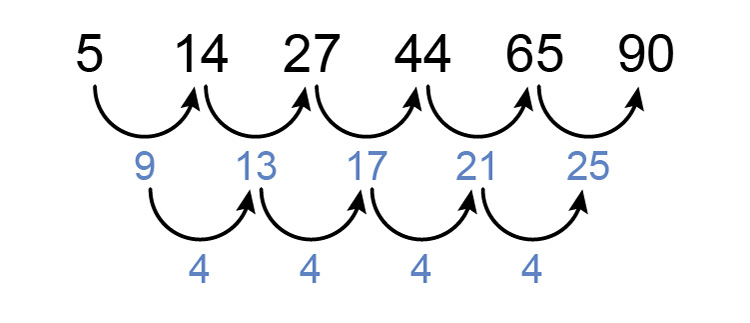
What is the 11th term of this sequence using method 1

The 1st term `=a+b+c`

so `5=a+b+c`

The 2nd term `=4a+2b+c`

so `14=4a+2b+c`

The 3rd term `=9a+3b+c`

so `27=9a+3b+c`

Now you have 3 simultaneous equations.

`5=a+b+c` .................... (1)

`14=4a+2b+c` ................ (2)

`27=9a+3b+c` ................ (3)

Now solve for one letter at a time

`5=a+b+c`

therefore `c=5-a-b`

Substitute this into equations (2) and (3).

`14=4a+2b+5-a-b`

`27=9a+3b+5-a-b`

These two simultaneous equations become

`14-5=4a-a+2b-b`

and `27-5=9a-a+3b-b`

Which simplify to

`9=3a+b` ............ (i)

and `22=8a+2b` .......... (ii)

Now we can solve these two simultaneous equations

`9=3a+b`

is the same as `b=9-3a`

substitute this into (ii)

`22=8a+2(9-3a)`

which is `22=8a+18-6a`

which is `22-18=8a-6a`

becomes `4=2a`

therefore `a=4/2=2`

Sustitute `a=2` into (i)

and `9=3a+b`

becomes `9=3times2+b`

`b=9-6=3`

Now substitute `a=2` and `b=3` into equation (1)

`5=a+b+c`

`5=2+3+c`

`c=0`

Summary `a=2` `b=3` and `c=0`

therefore the formula for the `n^(th)` term in this sequence is

`an^2+bn+c`

or `2n^2+3n+0`

which is `2n^2+3n`

Now we need to check the formula is correct

Try different values of `n` in the formula `2n^2+3n`

If `n=1` term `=2times1^2+3times1=2+3=5`

If `n=2` term `=2times2^2+3times2=8+6=14`

If `n=3` term `=2times3^2+3times3=18+9=27`

If `n=4` term `=2times4^2+3times4=32+12=44`

This is correct

The 11th term would be

If `n=11` then `2n^2+3n=2times11^2+3times11=242+33=275`

The 11th term `=275`