Sequence pattern 3 - multiples

The next pattern to look for in a sequence are multiples.

They also call this a geometric sequence or geometric progression.

`3`, `6`, `12`, `24`, `48`

Divide each term by the previous term

`6/3=2`, `12/6=2`, `24/12=2`, `48/24=2`

The multiple used is 2.

Example 1

What are the next two numbers in the following sequence?

`2`, `6`, `18`, `54`, `162`

Is it arithmetic - a consistent difference between numbers?

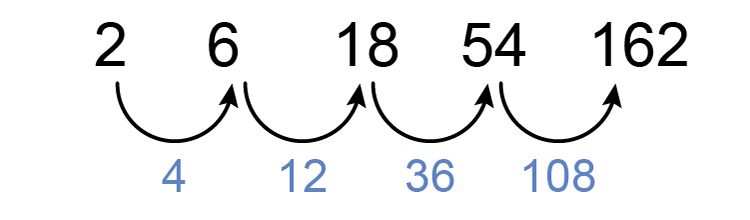
In multiplication sequences you are trying to find the difference of each number in the progression, it is not consistent because the numbers identified are different

No it's not

Is it quadratic - a consistent difference between differences?

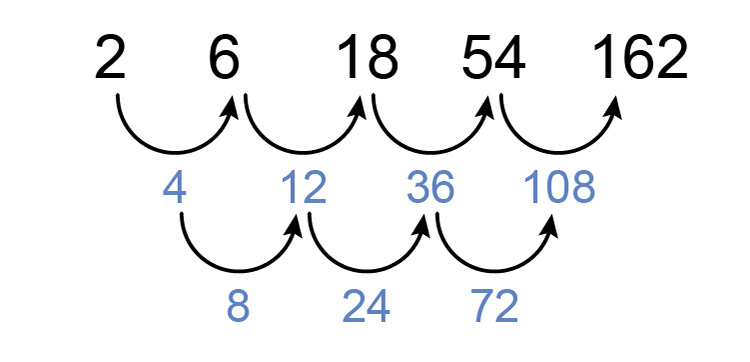
Does the sequence have consistent difference between differences no it does not because the differences between differences are all different

No it's not

Is it a multiple (or geometric sequence)?

`2`, `6`, `18`, `54`, `162`

Divide each term by the previous term

`6/2=3`, `18/6=3`, `54/18=3`, `162/54=3`

Yes, it is. It is a multiple of 3.

So the next two numbers are:

`162times3=486`

and the next would be

`486times3=1,458`

Example 2

What are the next two numbers in the following sequence?

`-2`, `4`, `-8`, `16`, `-32`, `64`

Is it arithmetic - a consistent difference between numbers?

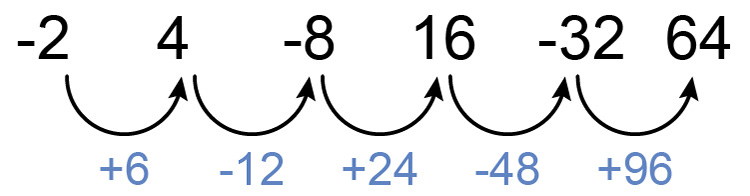
Is this example consistent…. No it is not, then is a multiplication sequence

No it's not

Is it a quadratic - a consistent difference between differences?

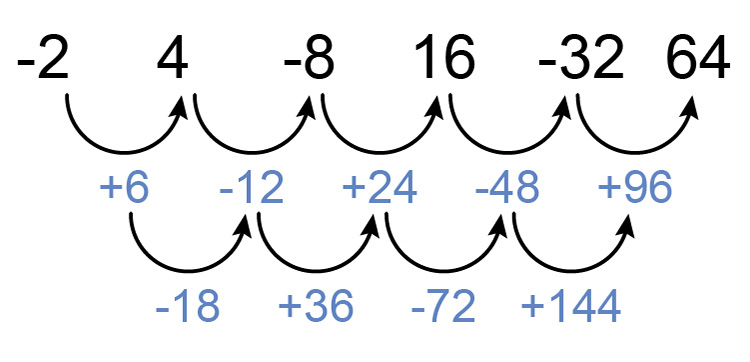
Does this example have consistent differences between differences no it does not

No it's not

Is it a multiple (or geometric sequence)?

`-2`, `4`, `-8`, `16`, `-32`, `64`

Divide each term by the previous term

`4/-2=-2`, `-8/4=-2`, `16/-8=-2`, `-32/16=-2`, `64/-32=-2`

Yes, it is. It is a multiple of `-2`.

So the next two numbers are:

`64times-2=-128`

and the next would be

`-128times-2=256`

Answer the next two numbers are `-128` and `256`

Example 3

What are the next two numbers in the following sequence?

`40`, `20`, `10`, `5`, `2.5`

Is it arithmetic - a consistent difference between numbers?

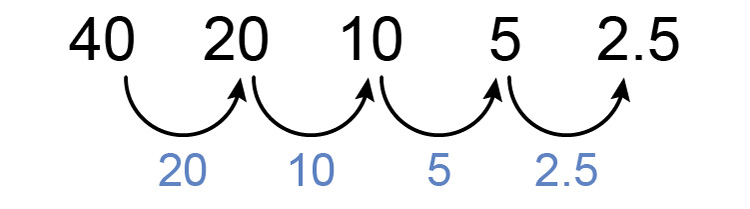
Is this example consistent…. No it is not, then is a multiplication sequence

No it's not

Is it quadratic - a consistent difference between differences?

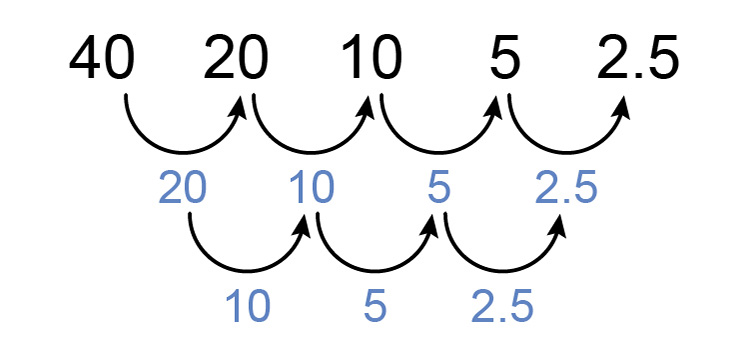
Does this example have consistent differences between differences no it does not

No it's not

Is it a multiple (or geometric sequence)?

`40`, `20`, `10`, `5`, `2.5`

Divide each term by the previous term

`20/40=0.5`, `10/20=0.5`, `5/10=0.5`, `2.5/5=0.5`

Yes, it is. It is a multiple of `0.5`.

So the next two numbers are:

`2.5times0.5=1.25`

and the next would be

`1.25times0.5=0.625`

Answer the next two numbers are `1.25` and `0.625`

Example 4

What are the next two numbers in the following sequence?

`3`, `3sqrt8`, `24`, `24sqrt8`

This is a trick because the only way to tackle this is to:

Try and keep the first two sequences going, which is
`3` and `3sqrt8`
Then you have to recognise that
`8=sqrt8timessqrt8`

So this sequence could be rewritten

`3`			`=3`
`3sqrt8`			`=3sqrt8`
`24`	`=`	`3timessqrt8timessqrt8` (i.e. `3times8=24`)	`=3sqrt8sqrt8`
`24sqrt8`	`=`	`(3timessqrt8timessqrt8)timessqrt8`	`=3sqrt8sqrt8sqrt8`

So the sequence can be rewritten as:

`3`, `3sqrt8`, `3sqrt8sqrt8`, `3sqrt8sqrt8sqrt8`

Now you can clearly see that dividing each term by the previous term gives

`(3sqrt8)/3=sqrt8`, `(3sqrt8sqrt8)/(3sqrt8)=sqrt8`, `(3sqrt8sqrt8sqrt8)/(3sqrt8sqrt8)=sqrt8`

So this is a multiple of `sqrt8`

The next two numbers in the sequence are

`3sqrt8sqrt8sqrt8timessqrt8=3times8times8=192`

and the next is

`3sqrt8sqrt8sqrt8sqrt8timessqrt8=3times8times8timessqrt8=192sqrt8`

Answer next two numbers are `192` and `192sqrt8`