Sequence pattern 2 - Consistent difference between differences

The next easiest pattern in a sequence to find is to look for a consistent difference between differences.

They also call this a quadratic sequence. (For a definition of quadratics see our mammoth memory quadratics section)

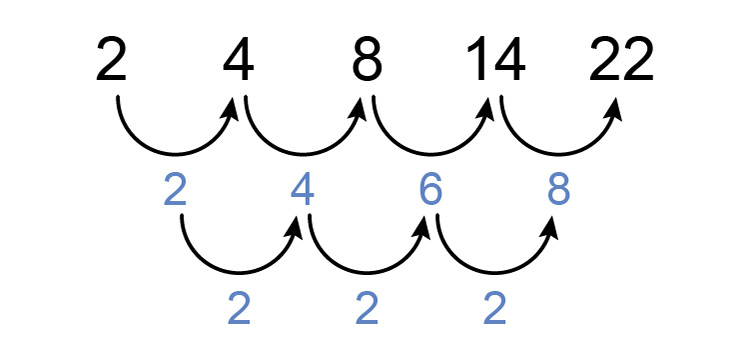
Consistent difference between differences first find the difference between the numbers in the sequence then find the difference of the differences identified this example is 2

There is a consistent difference between the differences of the original sequence and this is 2.

Quadratic `=x^2` Involved here (something to the power of 2)

Example 1

Find the pattern in the following sequence:

`7`, `9`, `13`, `19`, `27`

First, see if there is a consistent difference between each number.

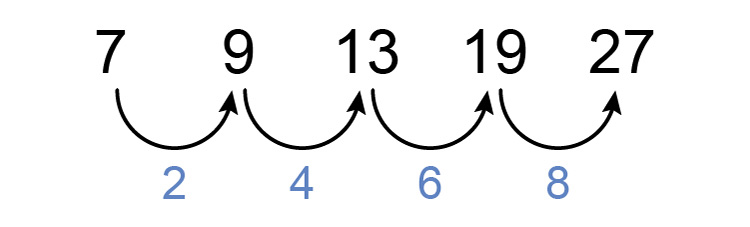
In this example first find the differences

There is not but now see if there is a constant difference between differences.

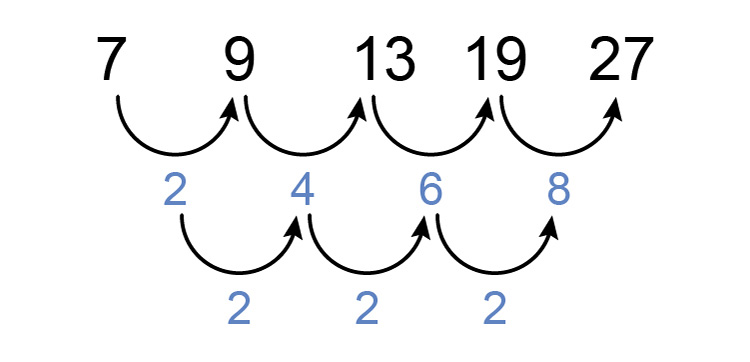
Then find the differences of the numbers you have just identified its 2

We can see that there is.

Answer = `2`

Example 2

Find the pattern in the following sequence:

`5`, `12`, `25`, `44`, `69`

First, see if there is a consistent difference between each number.

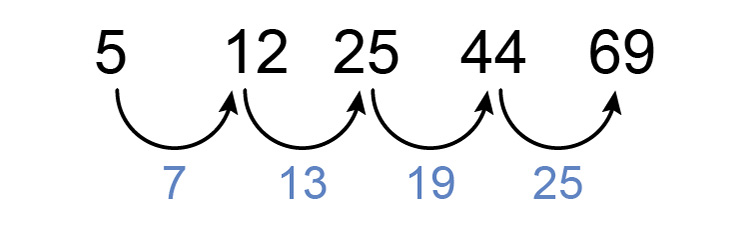
Find the differences in the sequence

There is not but now see if there is a constant difference between differences.

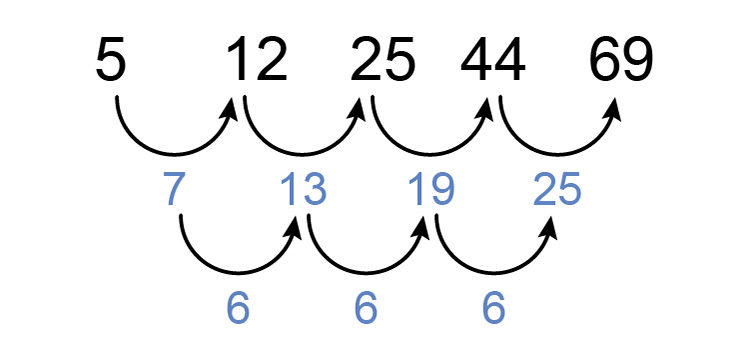
Find the differences of the numbers you have just identified its 6

We can see that there is.

Answer = `6`

Example 3

Find the pattern in the following sequence:

`-3`, `3`, `13`, `27`, `45`

First, see if there is a consistent difference between each number.

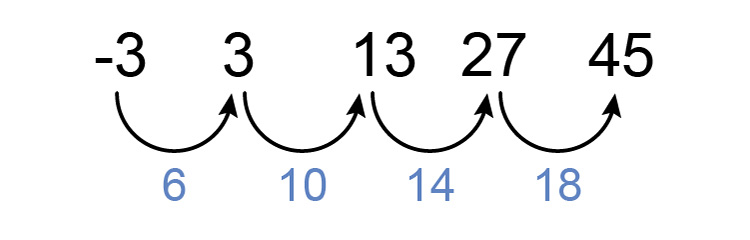
Find the differences in the sequence

There is not but now see if there is a constant difference between differences.

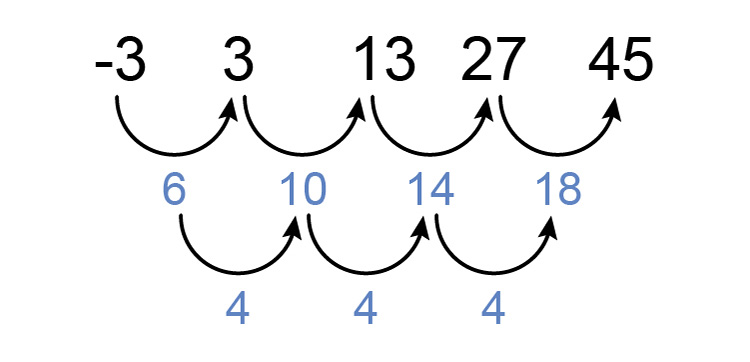
Find the differences of the numbers you have just identified its 4

We can see that there is.

Answer = `4`

Example 4

Find the pattern in the following sequence:

`0`, `0`, `2`, `6`, `12`

First, see if there is a consistent difference between each number.

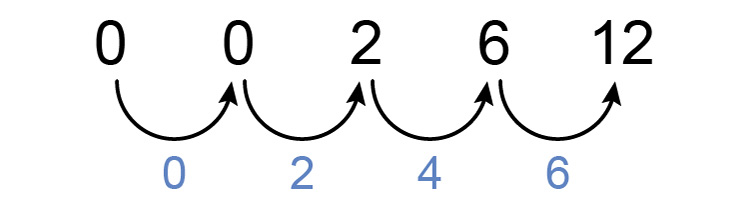
Find the differences in the sequence

There is not but now see if there is a constant difference between differences.

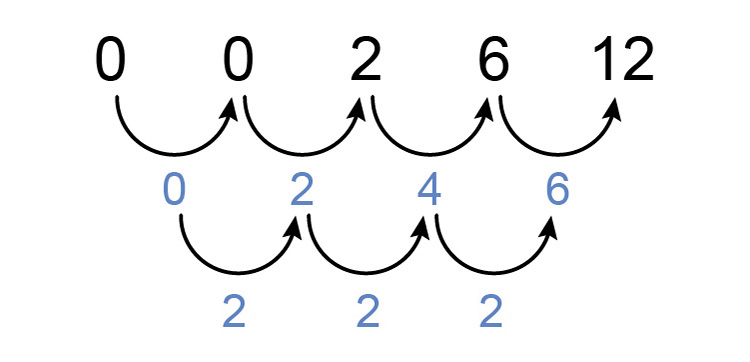
Find the differences of the numbers you have just identified its 4

We can see that there is.

Answer = `2`

Example 5

Find the pattern in the following sequence:

`1`, `11`, `20`, `28`, `35`

First, see if there is a consistent difference between each number.

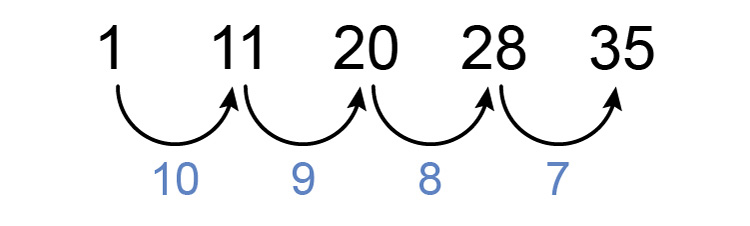
Find the differences in the sequence

There is not but now see if there is a constant difference between differences.

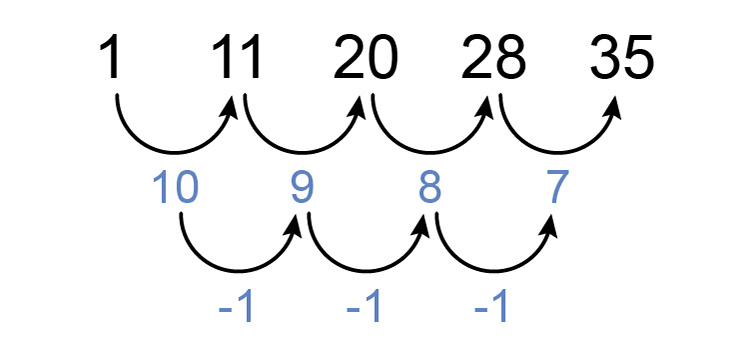
Find the differences of the numbers you have just identified its minus 1

We can see that there is.

Answer = `-1`