Arc of a sector
Using the same reasoning about radians we can also work out the length of any arc on a circle.
Example
Work out the length of the arc AB
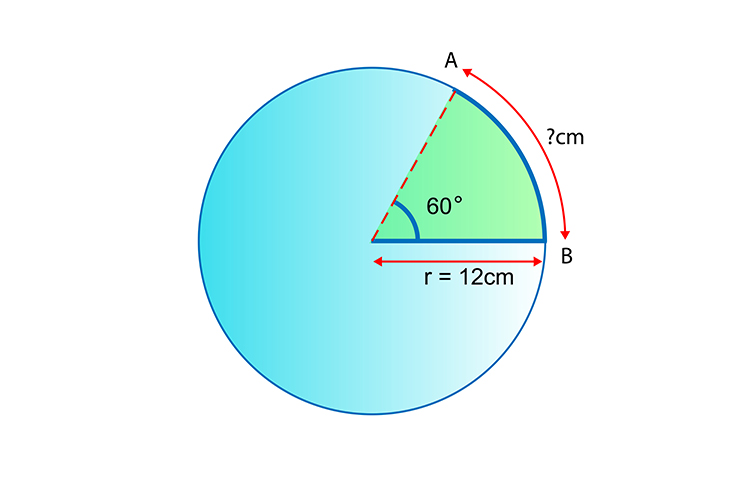
Circumference`=2pir`
Therefore Circumference`=2pi times12` `cm`
`=24pi` `cm`
Logic progresses as follows:
`24pi=100%`of the circumference
`360^@=24pi` `cm`
`60^@=x` `cm`
| `360/60` | `=` | `(24pi)/x` |
| `x` | `=` | `(60times24pi)/360` |
| `x` | `=` | `(1times24pi)/6` |
| `x` | `=` | `4pi` |
Answer: The arc is `x=4pi` `cm` long