The circumference of a circle experiment
Finding the circumference of a circle has many classrooms all over the world comparing the diameter of circle to their circumference:

Compare the circumference of the barrel to the diameter of the barrel.
Or in the snow:
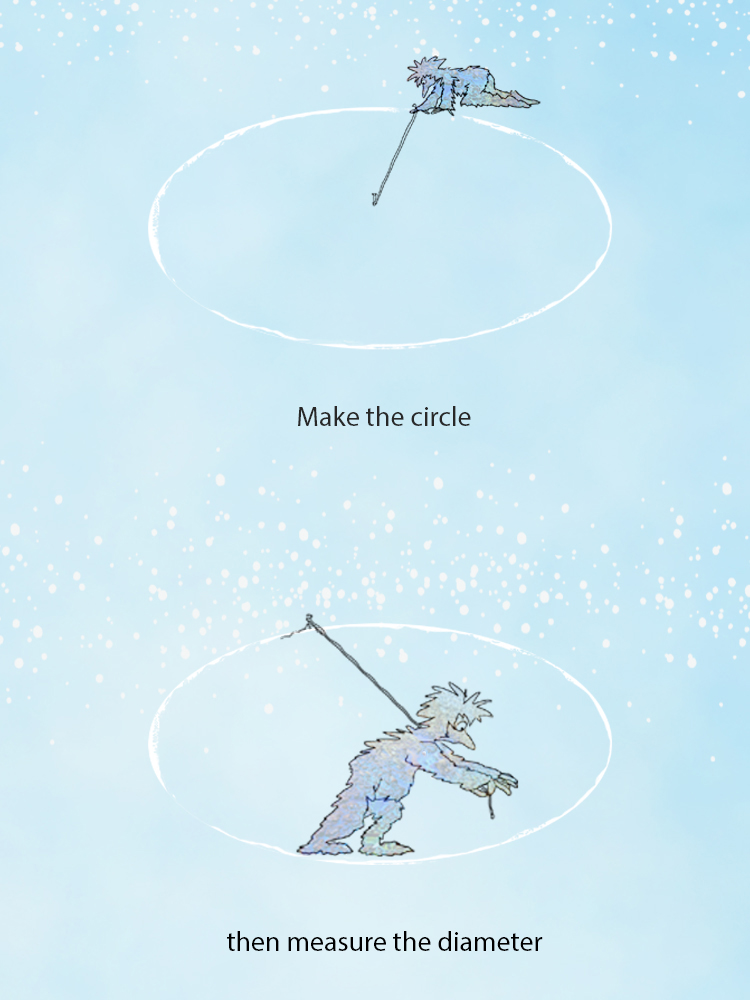
Compare the circumference of the circle in the snow with its diameter or rolling a car tyre.
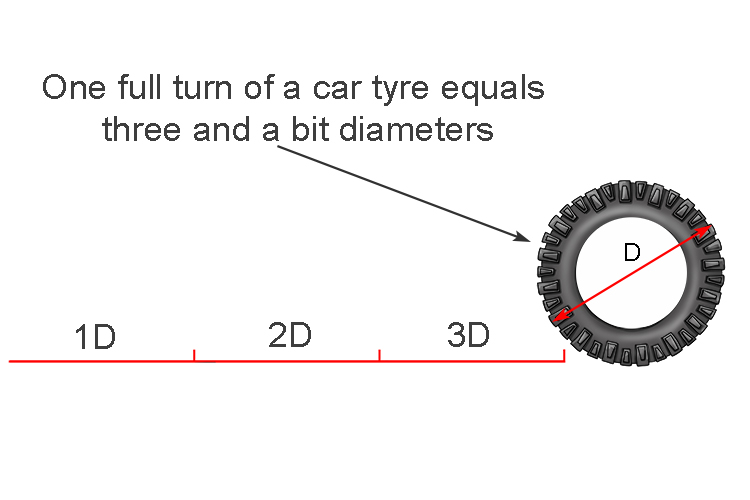
What every kid in the world has found is that
Roughly 3 diameters = The circumference
No matter what size of circle
To be more precise mathematicians found that the number of times the diameter goes around the perimeter is 3.141592…… and the number goes on forever.
Circumference = 3.142....times diameter
And to further confuse things mathematicians called this number 3.142…. Pi (pronounced Pie).
3.142....= Pi
And to confuse things even further they gave Pi the symbol π
Summary
Pi = `pi`
So the formula for circumference is
Circumference of a circle = 3.142….times diameter
Or
Circumference of a circle = `pitimesD`
NOTE 1:
`\piD` is the same as `2\pir`
NOTE 2:
Eventually, mathematicians also found the Area of the circle = `\pir^2`
Example 1
A tin of diameter 8 cm and height 15 cm has a label around it. The label is glued together using a 1 cm overlap. There is a 1 cm gap between the label and the top and the bottom of the tin.
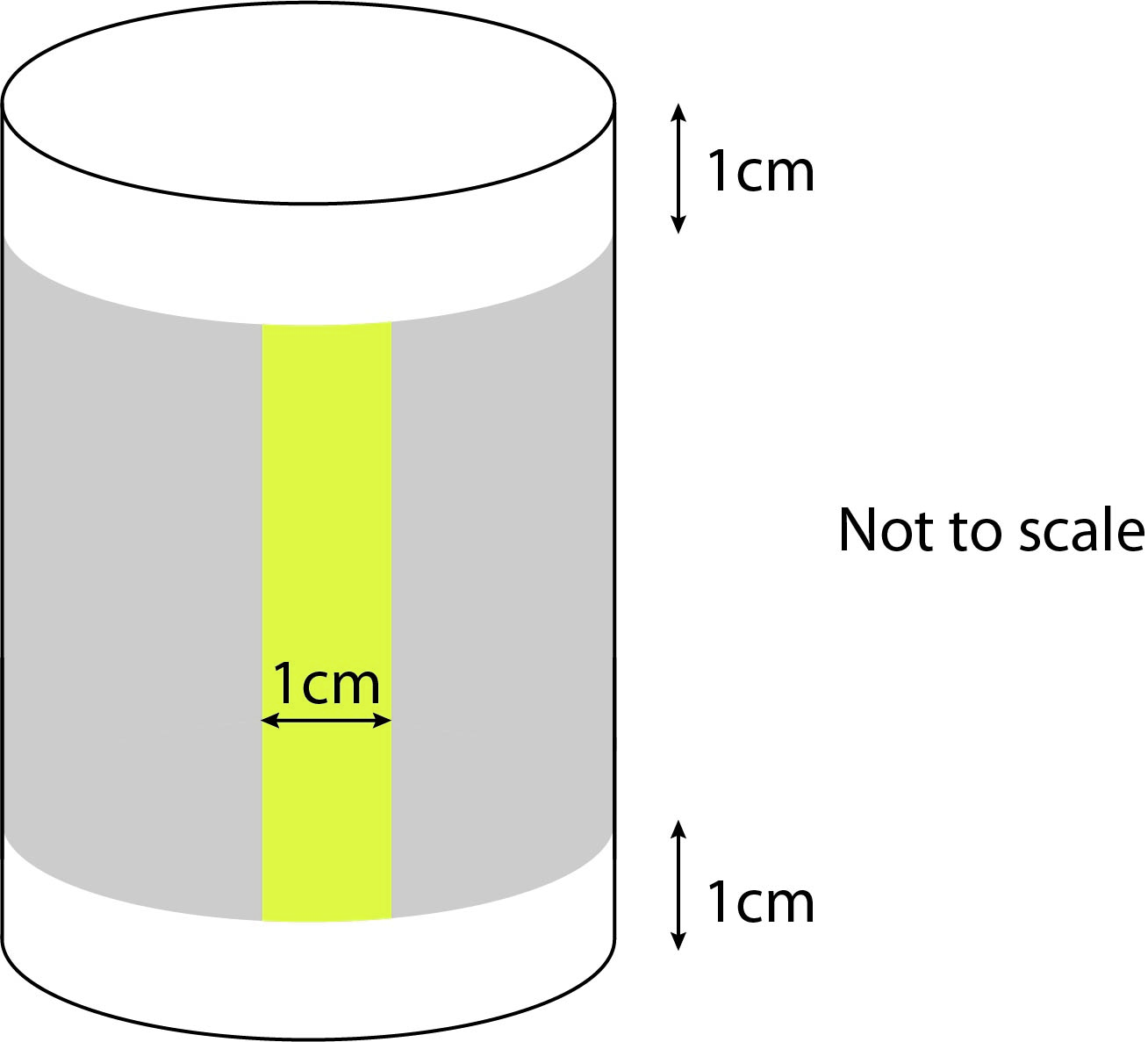
What length and height must the label be?
Answer:
Height of the label = Height of the can – gap at top and bottom.
Therefore height of the label `=15–(1\times\2)=15–2=13cm`
Length of the label = Circumference of the can + overlap
Therefore length of the label `=2\pir+1`
`r = 1/2\ diameter=1/2\times8=4`
Length of the label `=2\times\pi\times4+1`
Length of the label `=25.13+1=26.13cm`
Answer:
The label must be 26.13cm long and 13 cm high
Example 2
A factory makes novelty giant paper clips. A diagram of one is placed alongside a centimetre ruler as shown below. The curved ends are semicircles.
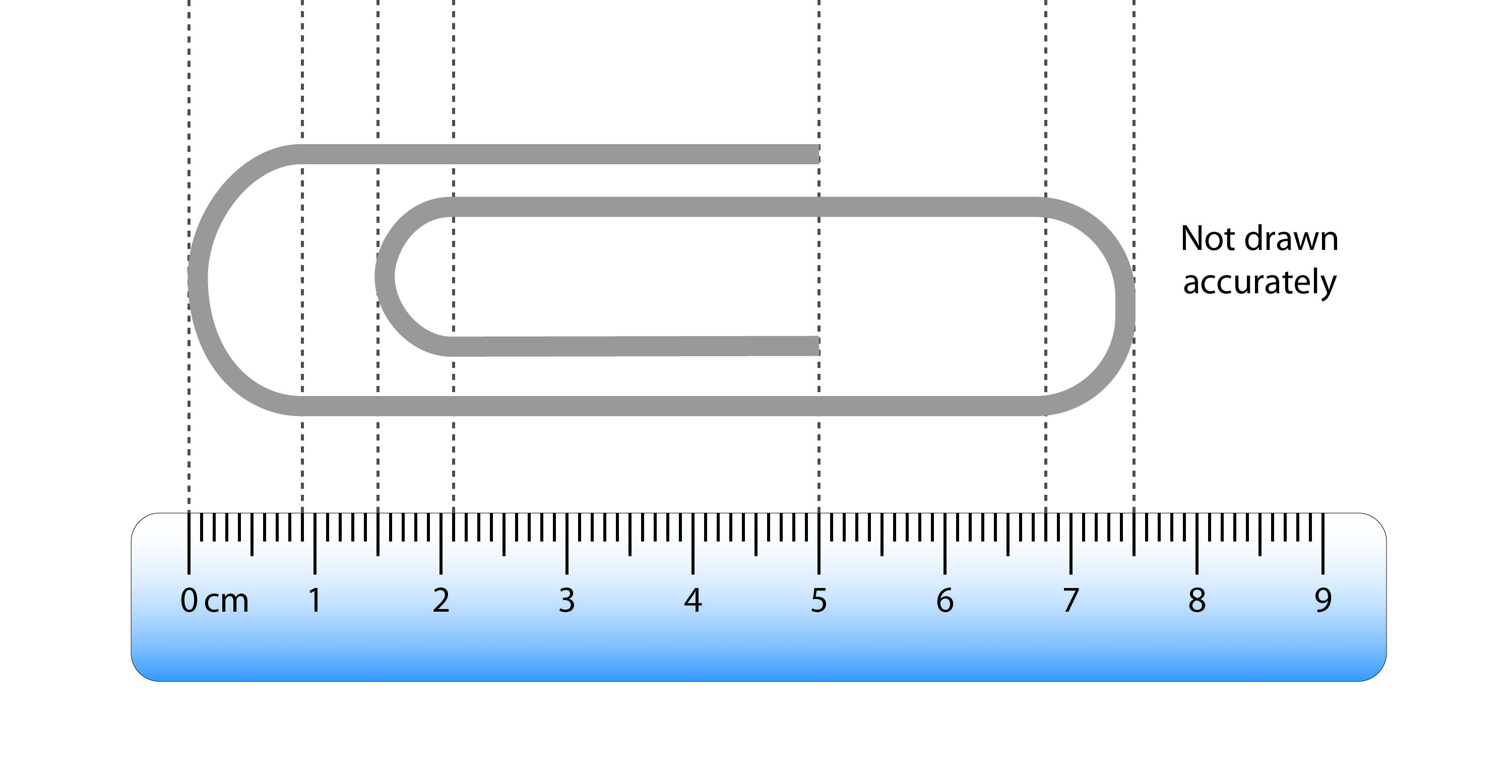
The paperclips are cut from rolls of coiled wire 1000m long. Calculate how many paper clips can be made from each roll of wire.
Answer:
We must first work out the length of wire required to make each paper clip.
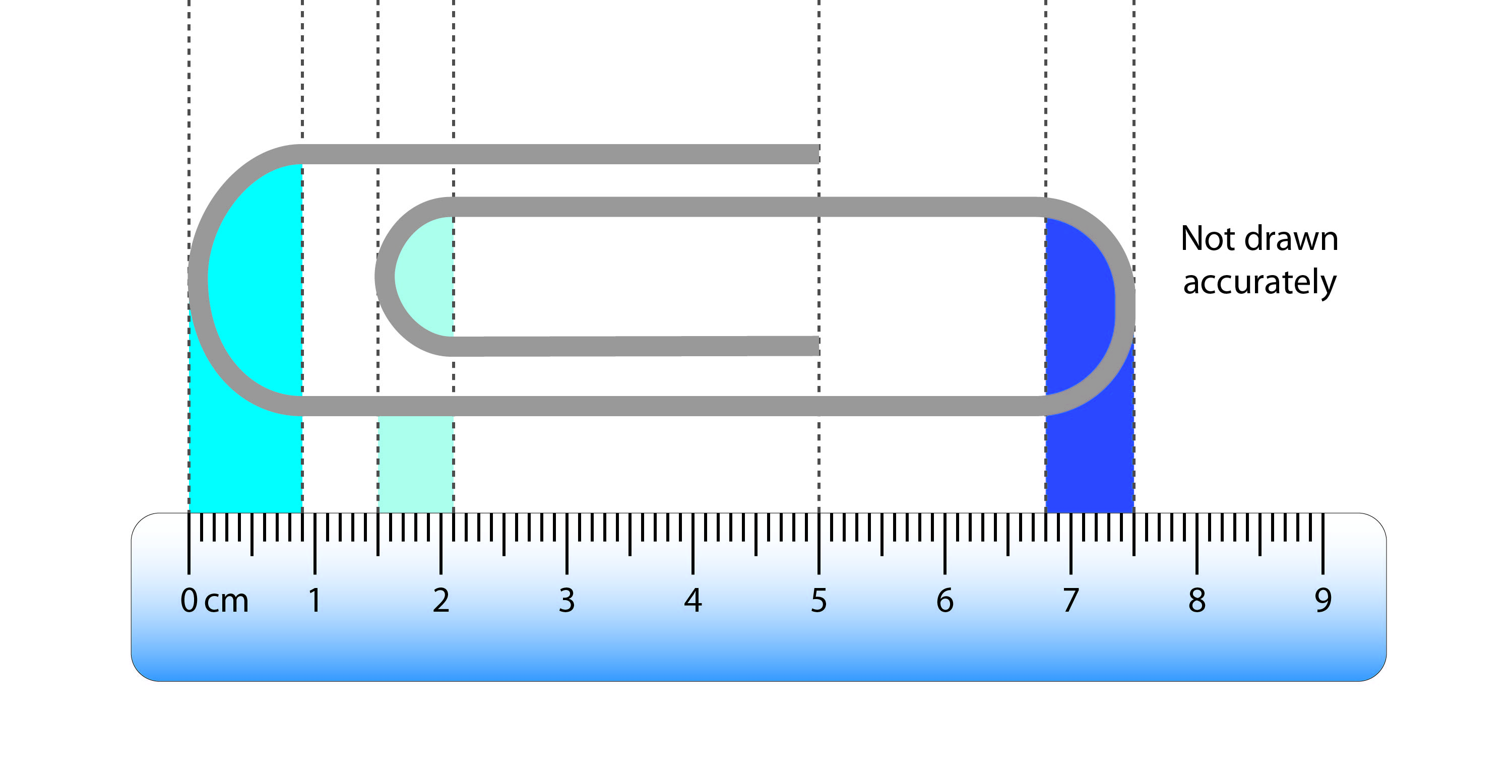
The length of wire needed for each paper clip is the total length of all the straight sections (coloured sections shown below) and the arc length of the three semi circles (coloured grey below).
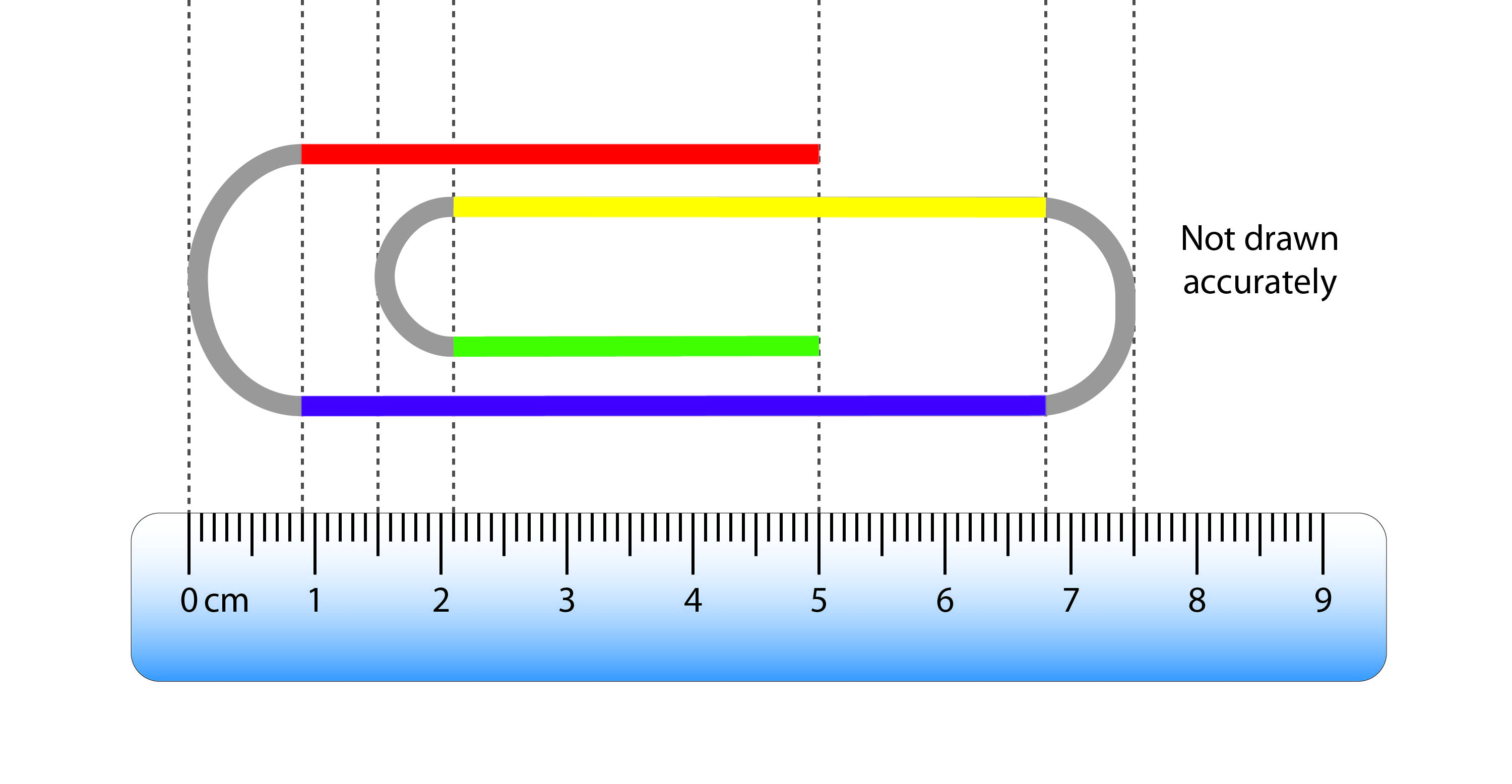
The length of the red straight section shown below is:
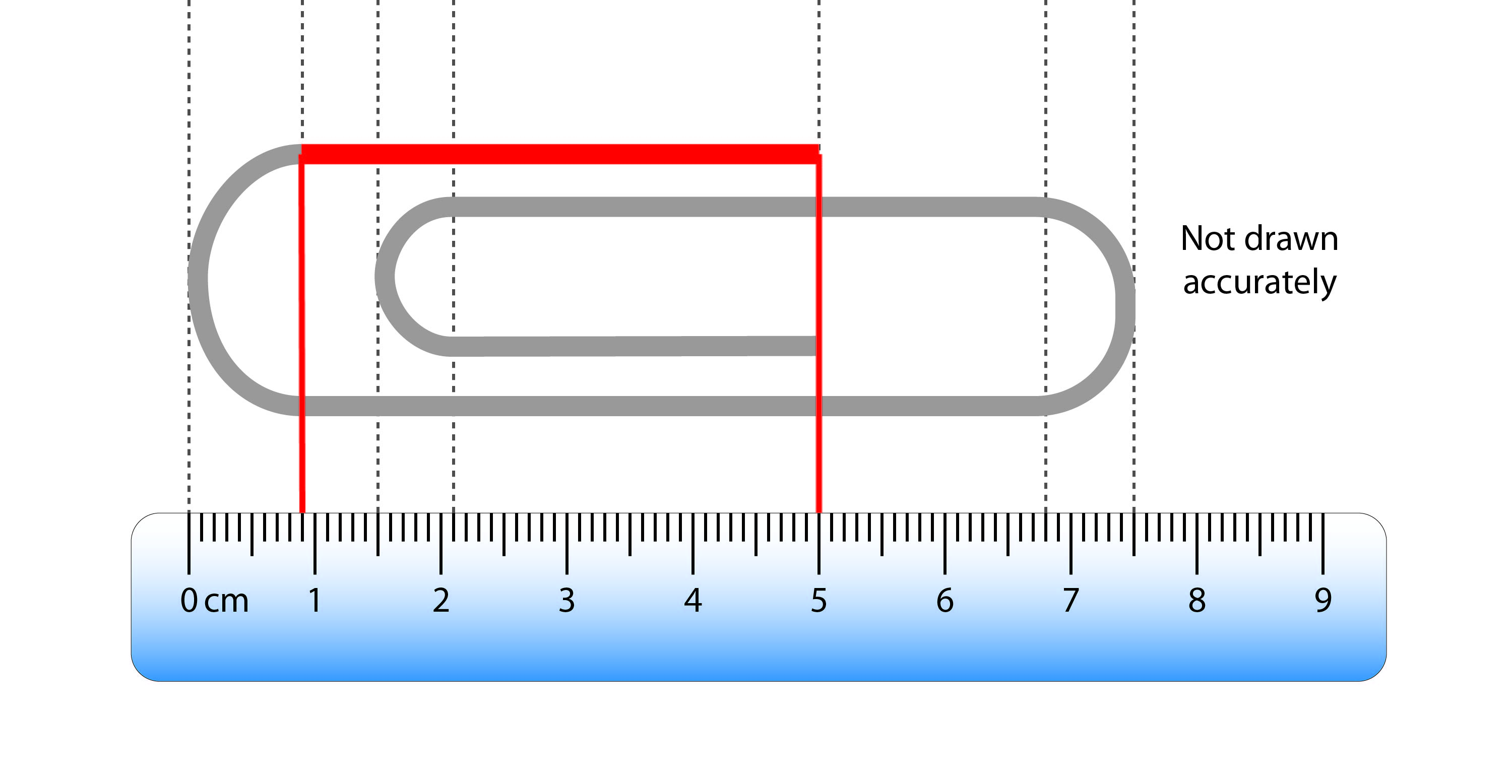
`5cm–0.9cm=4.1cm`
The length of the yellow straight section shown below is:
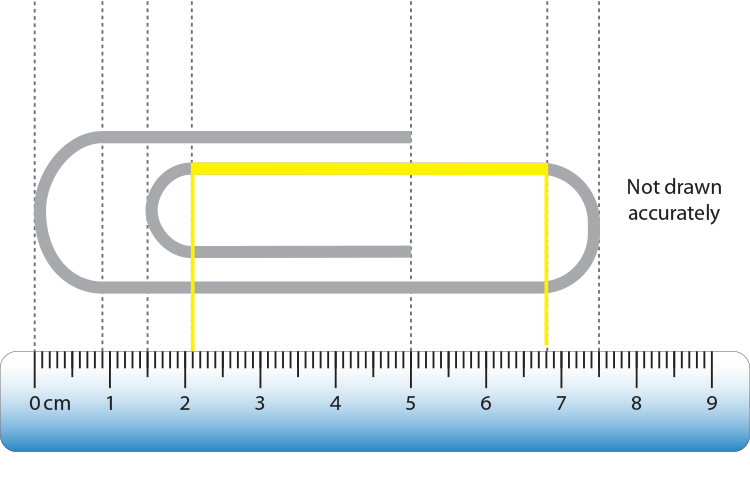
`6.8cm–2.1cm=4.7cm`
The length of the green straight section shown below is:
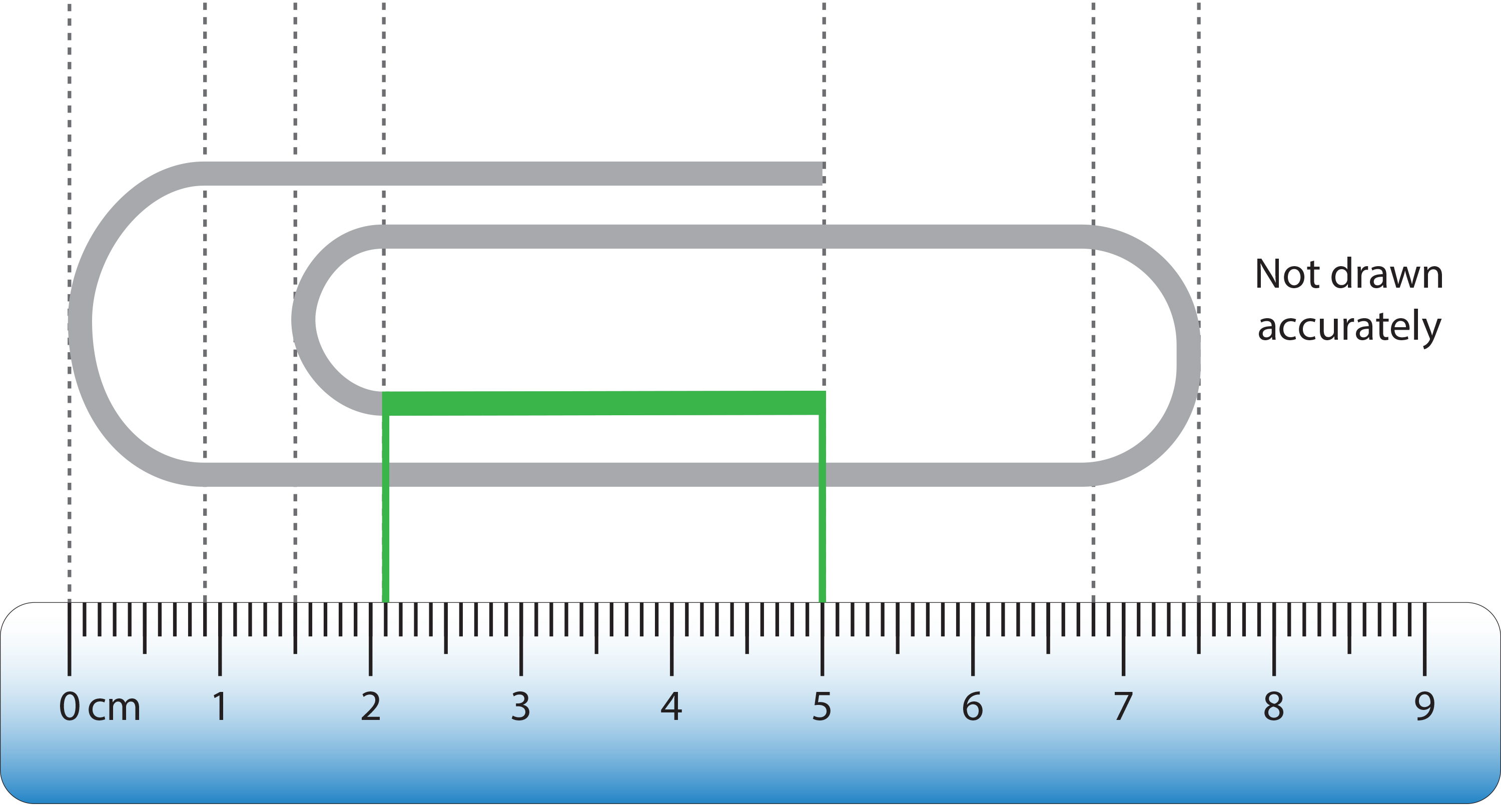
`5cm–2.1cm=2.9cm`
The length of the purple straight section shown below is:
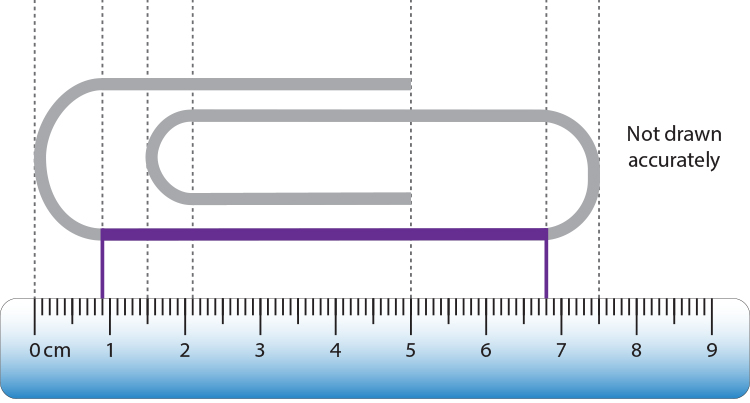
`6.8cm–0.9cm=5.9cm`
Therefore length of straight sections = red length + yellow length + green length + purple length
Length of straight sections `=4.1+4.7+2.9+5.9=17.6cm`
The length of the arc around a semicircle is half the circumference of the whole circle so if
A circles circumference `=2\pir`
Then a semi circles arc `=\pir`
The radius of the left hand semicircle on the paper clip shown below is:
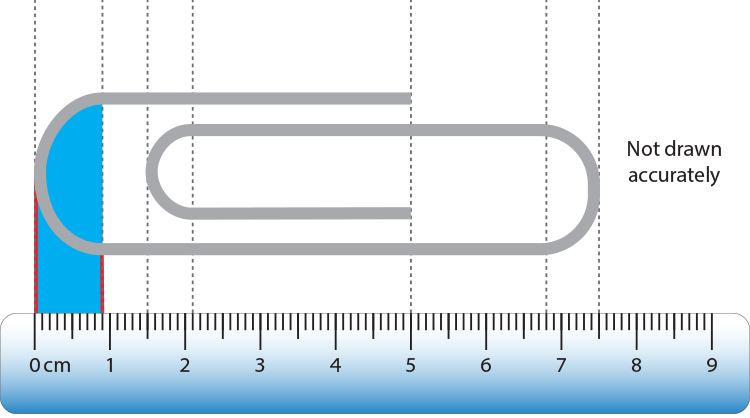
`0.9cm–0cm=0.9cm`
Therefore the arc length of this semicircle `=\pir=\pi\times0.9=2.8cm`
The radius of the middle semicircle on the paper clip shown below is:
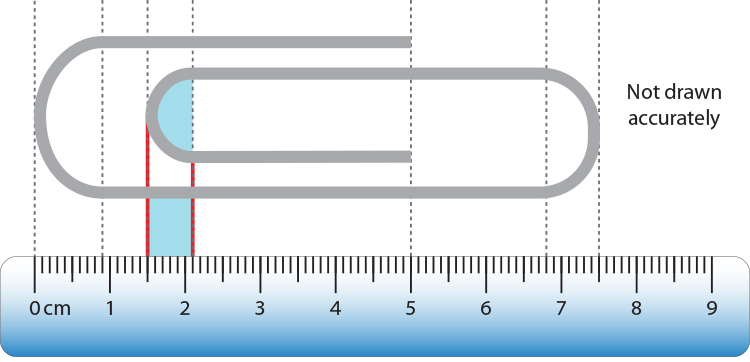
`2.1cm–1.5cm=0.6cm`
Therefore the arc length of this semicircle = `pir=pitimes0.6=1.9cm`
The radius of the right hand semicircle on the paper clip shown below is:
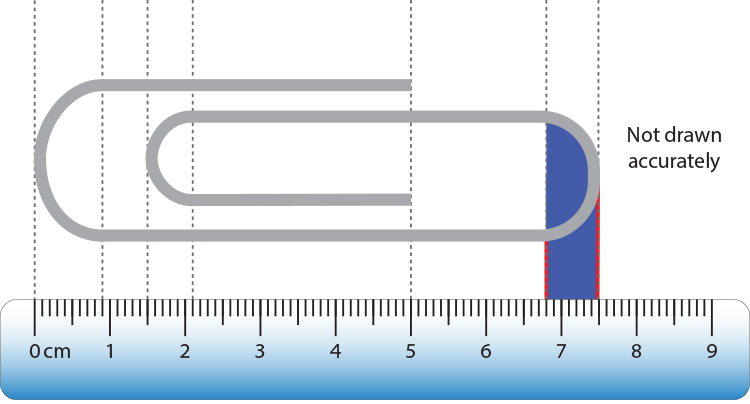
`7.5cm–6.8cm=0.7cm`
Therefore the arc length of this semicircle `=\pir=\pi\times\0.7=2.2cm`
So the total length of the arcs formed by the paper clips semi-circles `=2.8+1.9+2.2=6.9cm`
Therefore the total length of each paper clip = The total length of all the straight sections (17.6cm) plus the total arc lengths of the three semi circles (6.9cm) `= 17.6+6.9=24.5cm`
Each roll of coiled wire = 1000m and there are 100cm in 1m
Therefore each roll of coiled wire = `1000times100=100,000cm`
`(100,000)/(24.5)=4081.63`
Answer:
4081 paperclips can be made from each roll of wire.