Parabolas - Double the distance from the `y` axis

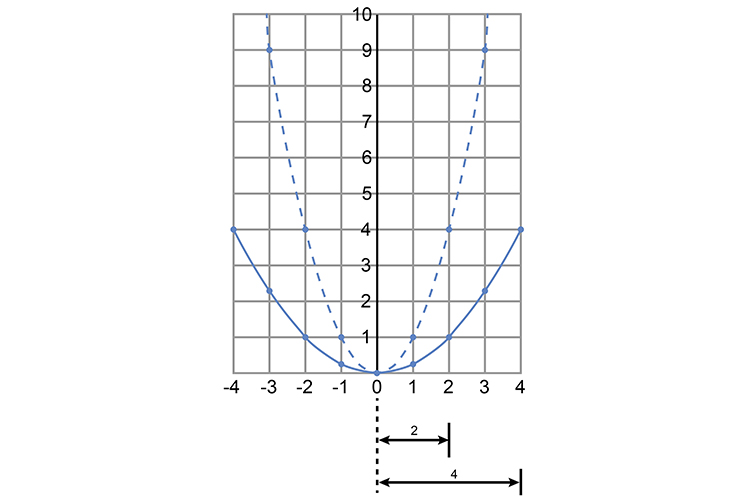
`y=(1/2x)^2` - Doubles the distance from the `y` axis.

To prove this, plot the graph.

Try different values of `x`

`x=4`		`y=(1/2times4)^2`	`=(2)^2`	`=4`
`x=3`		`y=(1/2times3)^2`	`=(1.5)^2`	`=2.25`
`x=2`		`y=(1/2times2)^2`	`=(1)^2`	`=1`
`x=1`		`y=(1/2times1)^2`	`=(1/2)^2`	`=0.25`
`x=0`		`y=(1/2times0)^2`	`=(0)^2`	`=0`
`x=-1`		`y=(1/2times(-1))^2`	`=(-1/2)^2`	`=0.25`
`x=-2`		`y=(1/2times(-2))^2`	`=(-1)^2`	`=1`
`x=-3`		`y=(1/2times(-3))^2`	`=(-1.5)^2`	`=2.25`
`x=-4`		`y=(1/2times(-4))^2`	`=(-2)^2`	`=4`

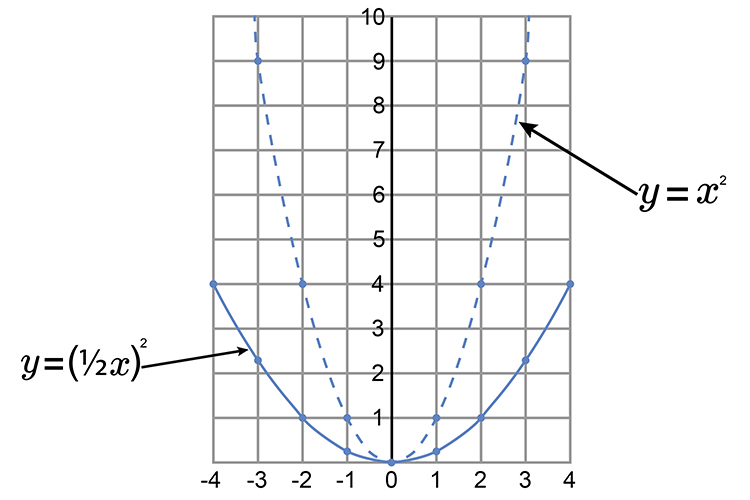
To reduce a parabola you need to double the distance from the y axis

Notice the parabola is double the distance from the `y` axis.

Notice the doubled distance of the example on the graph