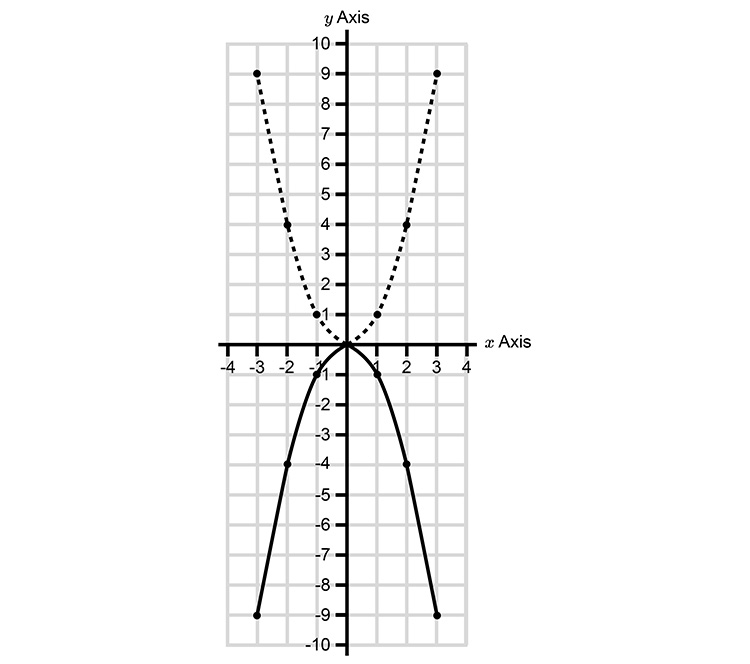
Reflecting simple parabolas
To reflect a parabola `y=x^2` through the `x` axis just place a negative sign in front of the `x^2`.
`y=-(x^2)` is a reflection of `y=x^2`
Multiply everything by `-1` and this gives you a reflection in the `x` axis only.
Think of a picture.
Example
Take `y=x^2` and reflect it
Reflecting `y=x^2` would give `y=-x^2`
To prove this plot both parabolas.
1st `y=x^2`
Try different values of `x` in the equation `y=x^2`
| `x=3` | then | `y=3^2` | `=9` |
| `x=2` | then | `y=2^2` | `=4` |
| `x=1` | then | `y=1^2` | `=1` |
| `x=0` | then | `y=0^2` | `=0` |
| `x=-1` | then | `y=(-1)^2` | `=1` |
| `x=-2` | then | `y=(-2)^2` | `=4` |
| `x=-3` | then | `y=(-3)^2` | `=9` |
And we plot this as
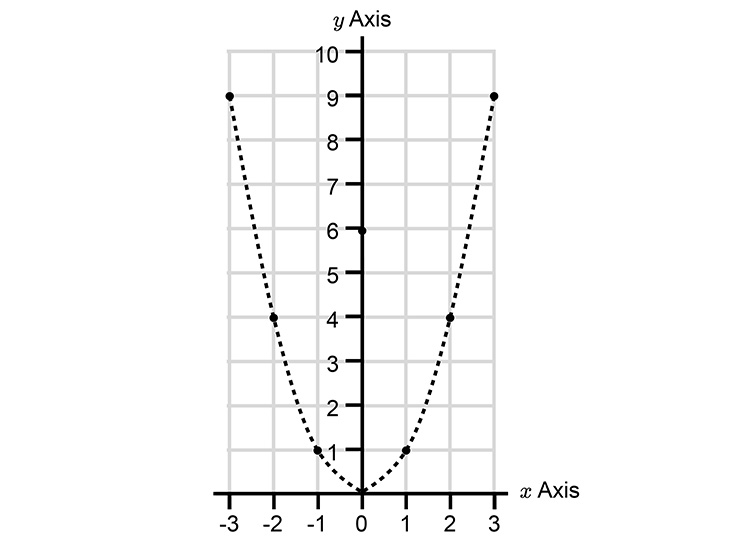
Now plot `y=-(x)^2`
NOTE:
`-(x)^2=-1times(x)^2`
Try different values of `x` in the equation `y=-x^2`
| `x=3` | `y=-1times3^2` | `=-9` | |
| `x=2` | `y=-1times2^2` | `=-4` | |
| `x=1` | `y=-1times1^2` | `=-1` | |
| `x=0` | `y=-1times0^2` | `=-0` | |
| `x=-1` | `y=-1times(-1)^2` | `=-1` | |
| `x=-2` | `y=-1times(-2)^2` | `=-4` | |
| `x=-3` | `y=-1times(-3)^2` | `=-9` |
Plotted on the same graph this would look like: