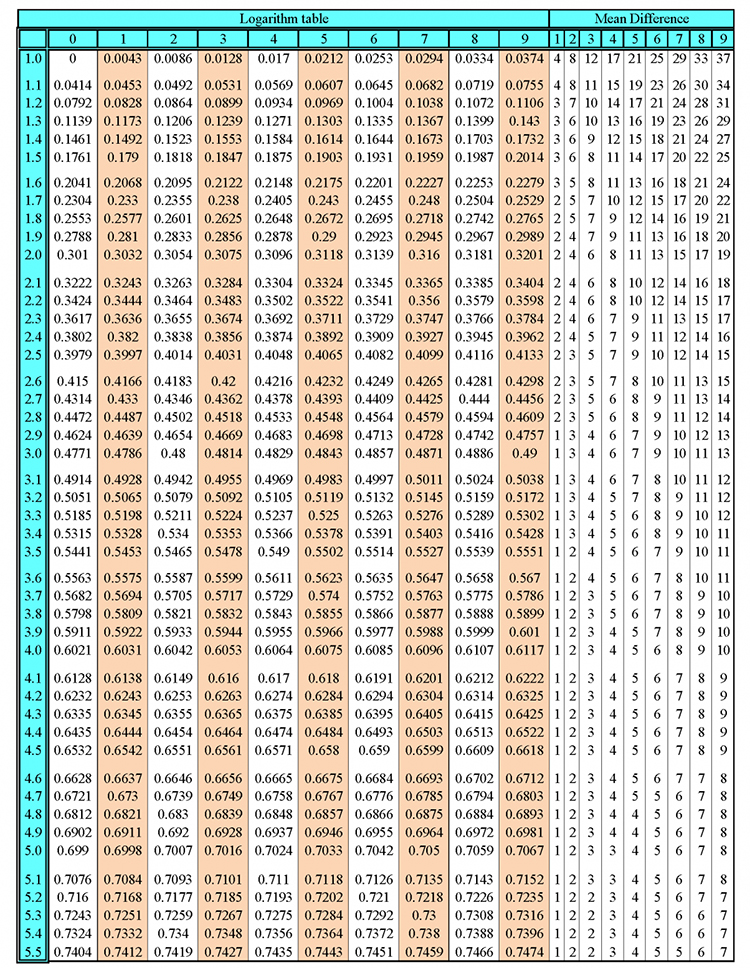
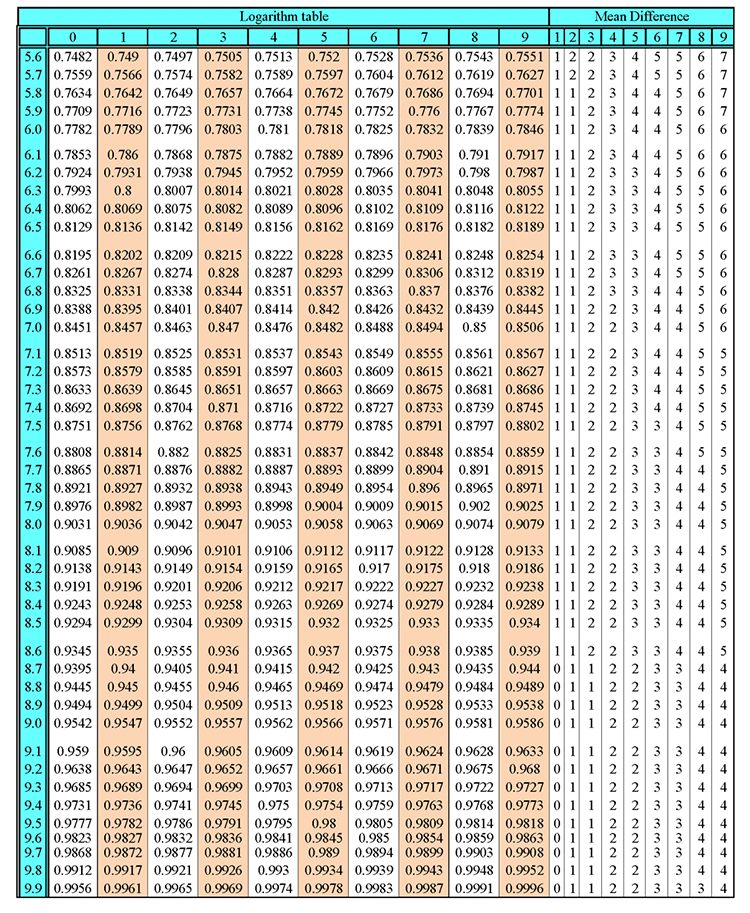
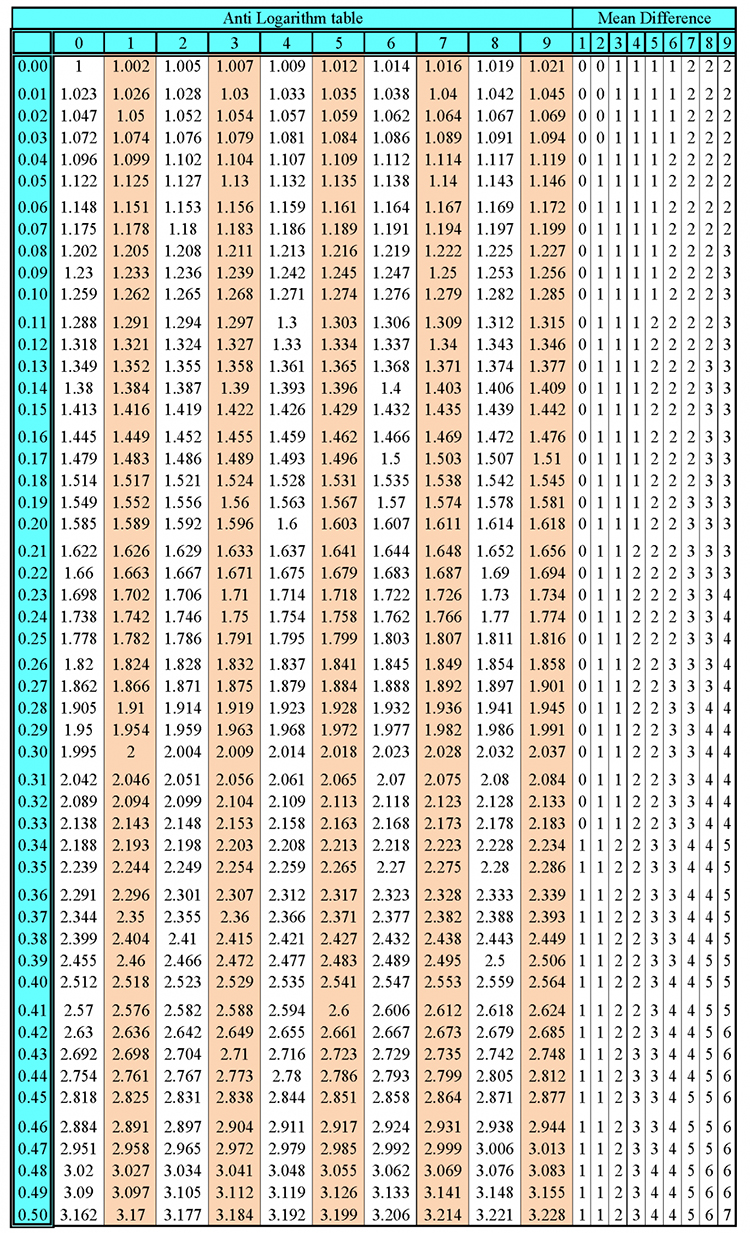
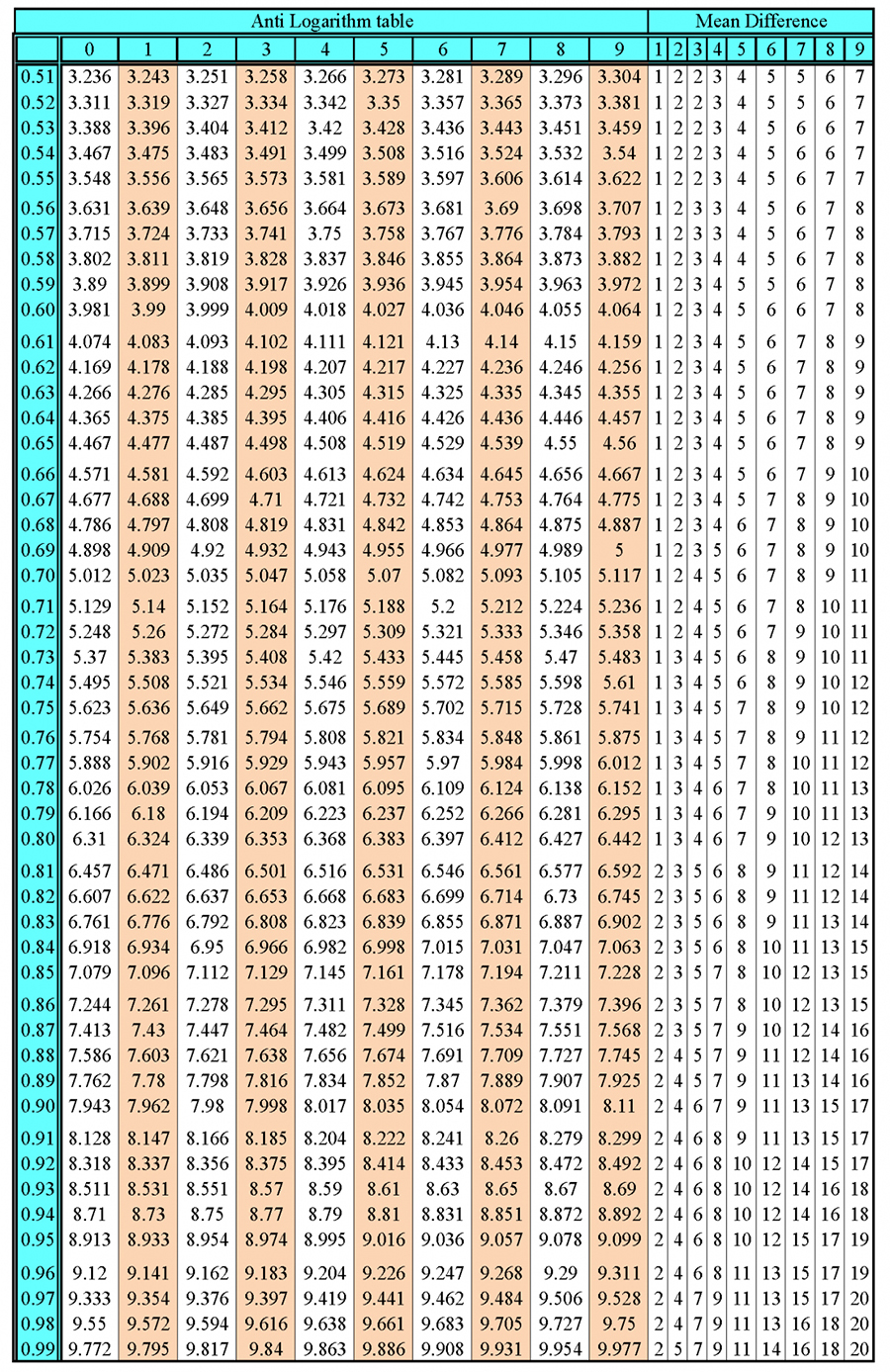
Rotating simple parabolas

Rotating `y=x^2` by 90° clockwise or anticlockwise you have to remember.

Rotate `y=x^2`        clockwise       `y=sqrtx`
Rotate `y=x^2`    anticlockwise    `y =sqrt(-x)`

So first plot `y=x^2`

Try different values of `x`

`x=3`		`y=3^2`	`=9`
`x=2`		`y=2^2`	`=4`
`x=1`		`y=1^2`	`=1`
`x=0`		`y=0^2`	`=0`
`x=-1`		`y=(-1)^2`	`=1`
`x=-2`		`y=(-2)^2`	`=4`
`x=-3`		`y=(-3)^2`	`=9`

 

And we plot this as

 

Now plot `y=sqrtx`

try different values of `x`

`x=0`		`y=sqrt0=0`
`x=1`		`y=sqrt1=+-1`	`=+1\ \ or\ -1`
`x=4`		`y=sqrt4=+-2`	`=+2\ \ or\ -2`
`x=9`		`y=sqrt9=+-3`	`=+3\ \ or\ -3`

 

Now plot `y=sqrt-x`

try different values of `x`

`x=0`		`y=sqrt(-1times0)=0`
`x=-1`		`y=sqrt(-1times-1)=sqrt1`	`=+1\ \ or\ -1`
`x=-4`		`y=sqrt(-1times-4)=sqrt4`	`=+2\ \ or\ -2`
`x=-9`		`y=sqrt(-1times-9)=sqrt9`	`=+3\ \ or\ -3`

 

Now plot this against the original graph. 

 

More Info