Translating parabolas

If you translate (slide) a parabola there are four elements you need to remember:

Start with the most famous parabola.

`y=x^2`

1. `y=x^2+1` Goes up `uarr` (Shifts the parabola up)

2. `y=x^2-1` Goes down `darr` (Shifts the parabola down)

3. `y=(x+1)^2` Goes left `larr` (Shifts the parabola to the left)

4. `y=(x-1)^2` Goes right `rarr` (Shifts the parabola to the right)

How do you remember translating parabolas:

Draw a diagonal line as in a graph

To start with draw a diagonal line of a graph

Then write

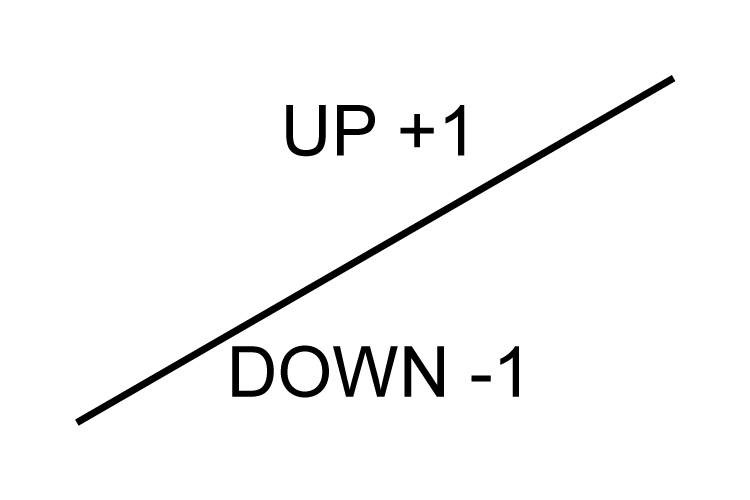
Write up above down

Then write

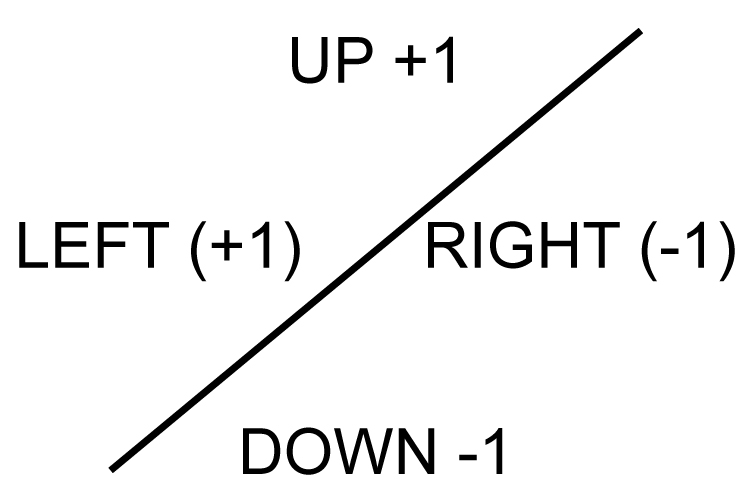
Up and left is positive, down and right is minus

This should remind you.

UP `+1`		`y=x^2+1`
Down `-1`		`y=x^2-1`
Right `(-1)`		`y=(x-1)^2`
Left `(+1)`		`y=(x+1)^2`

The results would be as the following examples:

Example 1

`y=x^2+1` or Up `+1`

And we can prove this or further help to remember this by plotting the graph out as follows:

`x=3`	`y=3^2+1`	`=9+1`	`=10`
`x=2`	`y=2^2+1`	`=4+1`	`=5`
`x=1`	`y=1^2+1`	`=1+1`	`=2`
`x=0`	`y=0^2+1`	`=0+1`	`=1`
`x=-1`	`y=(-1)^2+1`	`=1+1`	`=2`
`x=-2`	`y=(-2)^2+1`	`=4+1`	`=5`
`x=-3`	`y=(-3)^2+1`	`=9+1`	`=10`

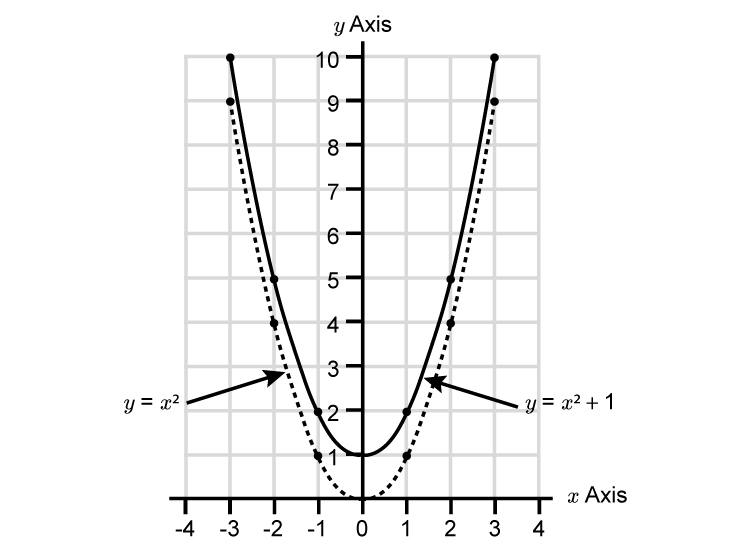
Transition a parabola down example 1

The parabola has been translated by `((0),(1))`

UP `+1\ \ uarr`

Example 2

`y=x^2-1` or Down `-1`

Again we can prove this or further help to remember this by plotting the graph as follows:

`x=3`	`y=3^2-1`	`=9-1`	`=8`
`x=2`	`y=2^2-1`	`=4-1`	`=3`
`x=1`	`y=1^2-1`	`=1-1`	`=0`
`x=0`	`y=0^2-1`	`=0-1`	`=-1`
`x=-1`	`y=(-1)^2-1`	`=1-1`	`=0`
`x=-2`	`y=(-2)^2-1`	`=4-1`	`=3`
`x=-3`	`y=(-3)^2-1`	`=9-1`	`=8`

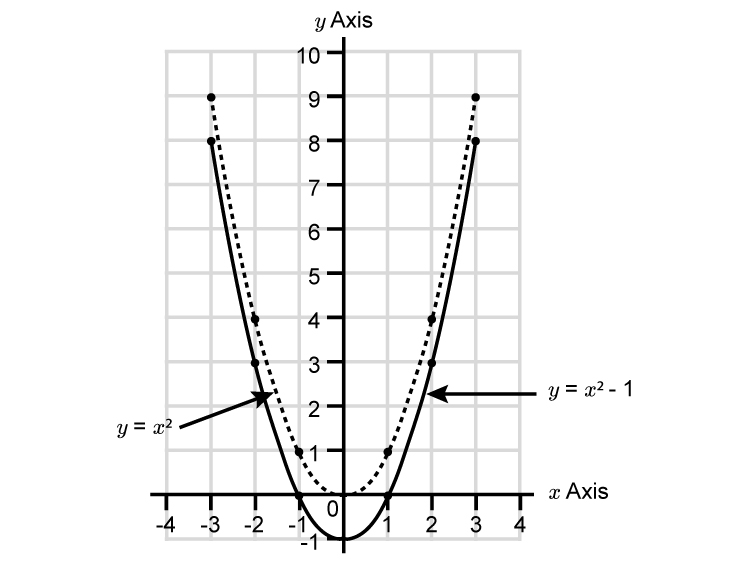
Transition a parabola down example 2

The parabola has been translated by `((0),(1))`

Down `-1\ \ darr`

Example 3

`y=(x+1)^2` or Left `larr`

NOTE:

See how we added brackets around the `x` value and added `+1`

We can prove this or further help remember this by plotting the graph as follows:

`x=3`	`y=(3+1)^2`	`=4^2`	`=16`
`x=2`	`y=(2+1)^2`	`=3^2`	`=9`
`x=1`	`y=(1+1)^2`	`=2^2`	`=4`
`x=0`	`y=(0+1)^2`	`=1^2`	`=1`
`x=-1`	`y=(-1+1)^2`	`=0^2`	`=0`
`x=-2`	`y=(-2+1)^2`	`=(-1)^2`	`=1`
`x=-3`	`y=(-3+1)^2`	`=(-2)^2`	`=4`
`x=-4`	`y=(-4+1)^2`	`=(-3)^2`	`=9`

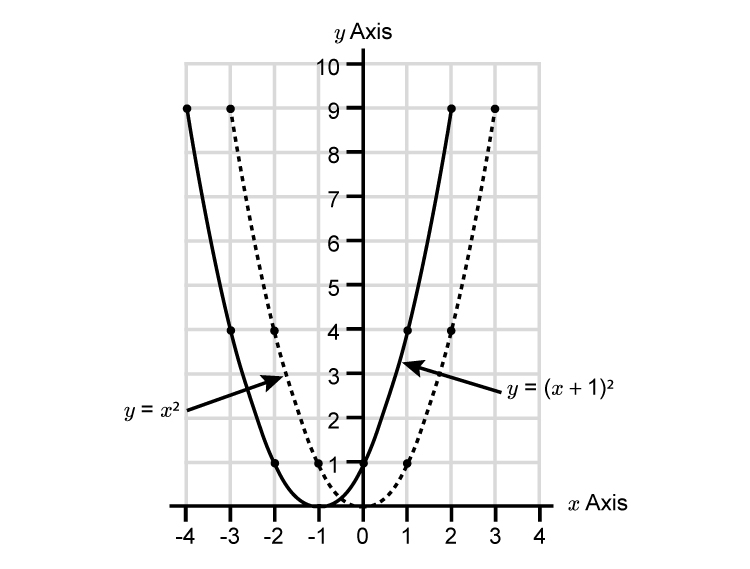
Transition a parabola to the left example 3

The parabola has been translated by `((-1),(0))`

Left `-1\ \ larr`

Example 4

`y=(x-1)^2` or Right `rarr`

NOTE:

See how we added brackets around the `x` value and subtracted `1`

We can prove this or further help remember this by plotting the graph as follows:

`x=4`	`y=(4-1)^2`	`=3^2`	`=9`
`x=3`	`y=(3-1)^2`	`=2^2`	`=4`
`x=2`	`y=(2-1)^2`	`=1^2`	`=1`
`x=1`	`y=(1-1)^2`	`=0^2`	`=0`
`x=0`	`y=(0-1)^2`	`=(-1)^2`	`=1`
`x=-1`	`y=(-1-1)^2`	`=(-2)^2`	`=4`
`x=-2`	`y=(-2-1)^2`	`=(-3)^2`	`=9`
`x=-3`	`y=(-3-1)^2`	`=(-4)^2`	`=16`

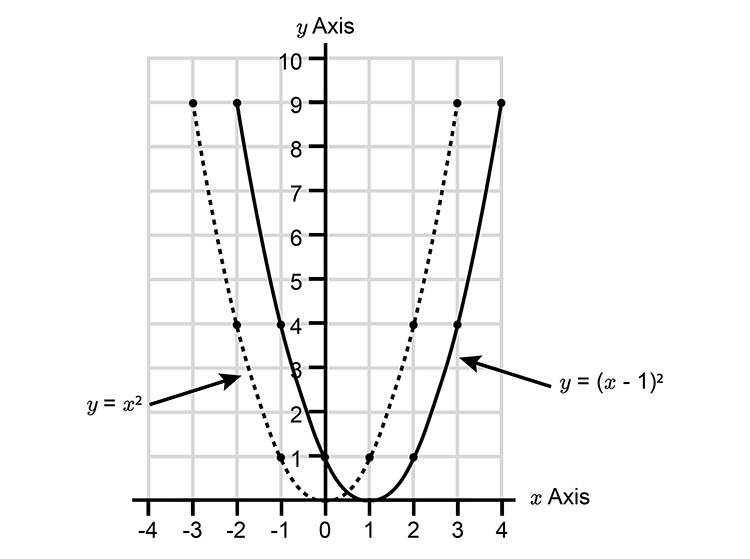
Transition a parabola to the right example 4

The parabola has been translated by `((1),(0))`

Right `+1\ \ rarr`