Slanting triangles

Even for triangles shaped as below, the area of a triangle = base x height and half it.

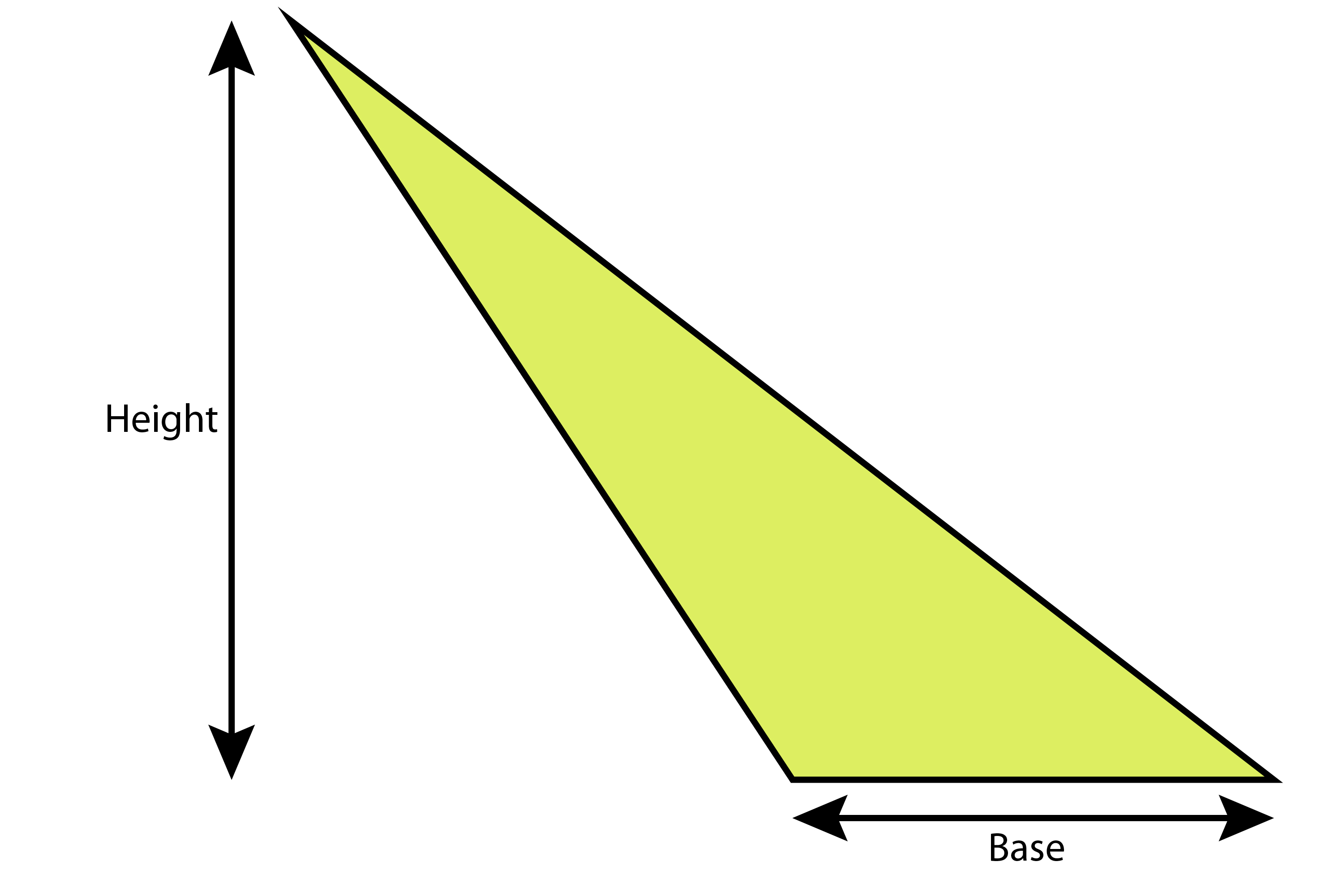
Even for slanting triangles and other triangles which are not right angle triangles, its half base times height

The proof (but you don’t need it) is as follows:

Redraw the above diagram

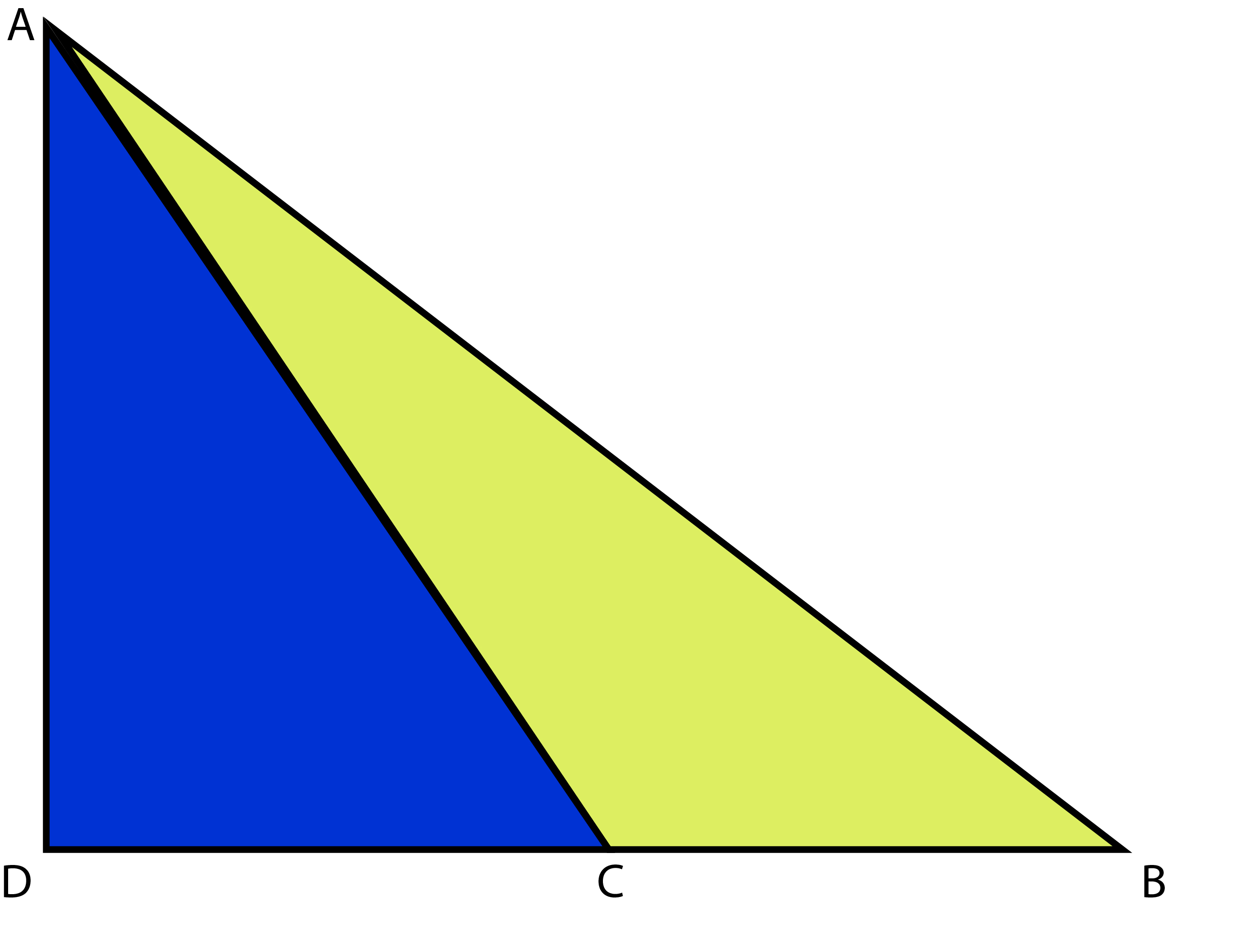
Turning the slanting triangle here into a right angle triangle makes working out the area a lot easier to understand

Area of triangle $ABC=$ Area triangle $ADB-$ Area triangle $ADC$

Area of triangle $ABC=1/2timesDBtimesAD-1/2timesDCtimesAD$

You can remove $1/2AD$

Area of triangle $ABC=1/2AD(DB-DC)$

And because $DB-DC=CB$

We can now say:

Area of triangle $ABC=1/2ADtimesCB$

NOTE:

Slanting triangles are rare and it’s still best to think of areas of triangles in a rectangle.