How do you know?

Divide the internal angles of a shape by 360, if it equals a whole number it will tessellate

If you can divide `360^@` exactly by an inside angle of a regular shape and get a whole number it can form a tessellation pattern.

Triangle

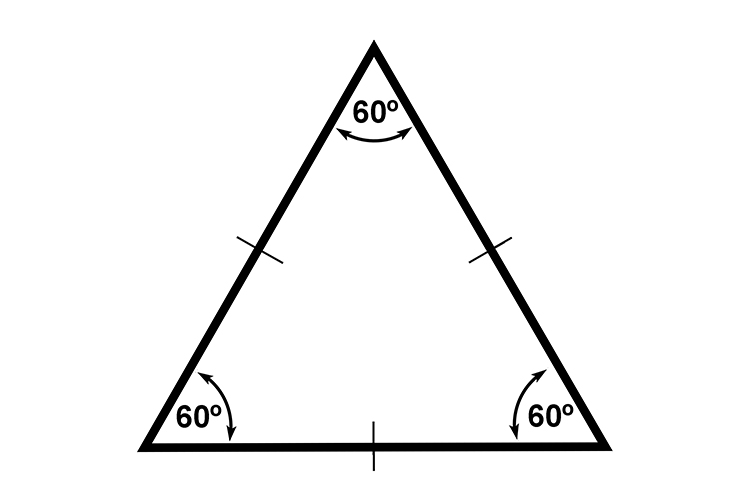
The internal angles of a triangle divided by 360 makes 6, this is a whole number so triangles will tessellate

`360/60=6`

(6 is a whole number)

Answer:

6 therefore this triangle can form a tessellation.

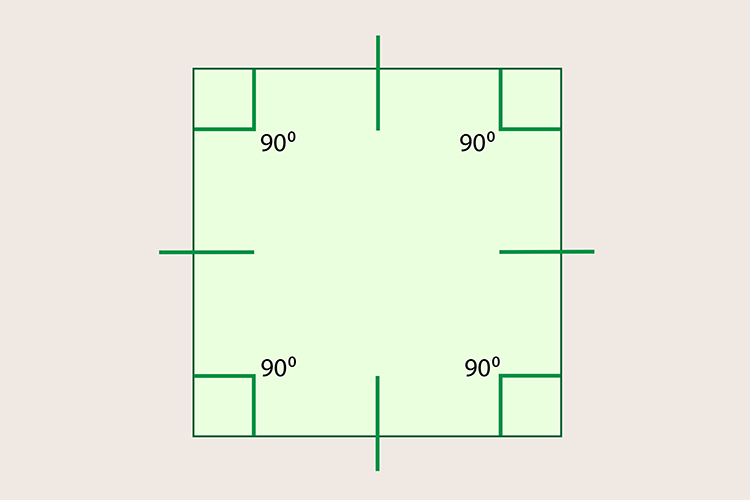
The internal angles of a square divided by 360 makes 4 this a whole number meaning it will tessellate

`360/90=4`

(4 is a whole number)

Answer:

A square can form a tessellation.

The internal angles of a pentagon divided by 360 makes 3.33, this is not a whole number meaning it will not tessellate

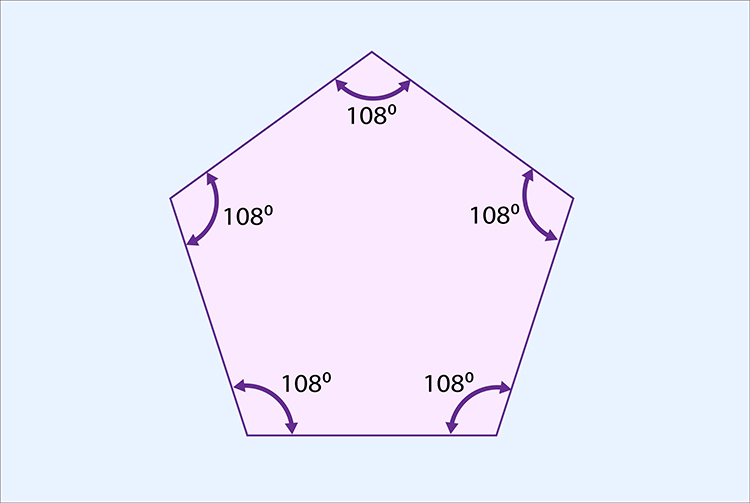
`360/108=3.33`

(3.33 is NOT a whole number)

Answer:

A pentagon can NOT form a tessellation.

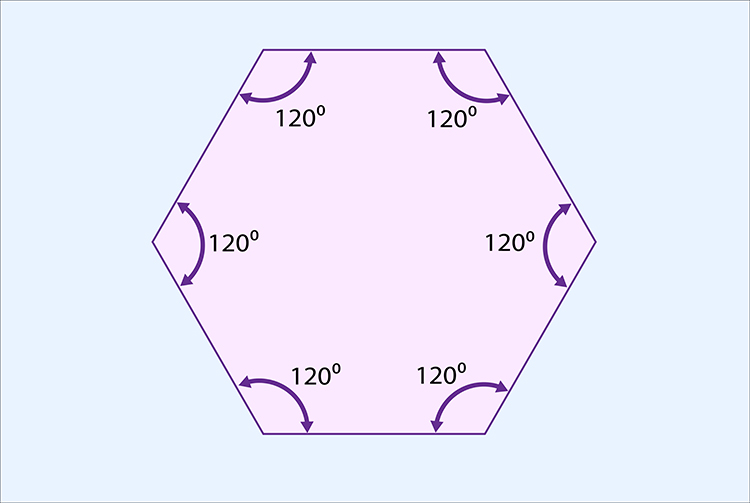
The internal angles of a hexagon divided by 360 makes 3, this is a whole number meaning it will tessellate

`360/120=3`

Answer:

A hexagon can be tessellated.