Tessellations and graph questions
Example 1
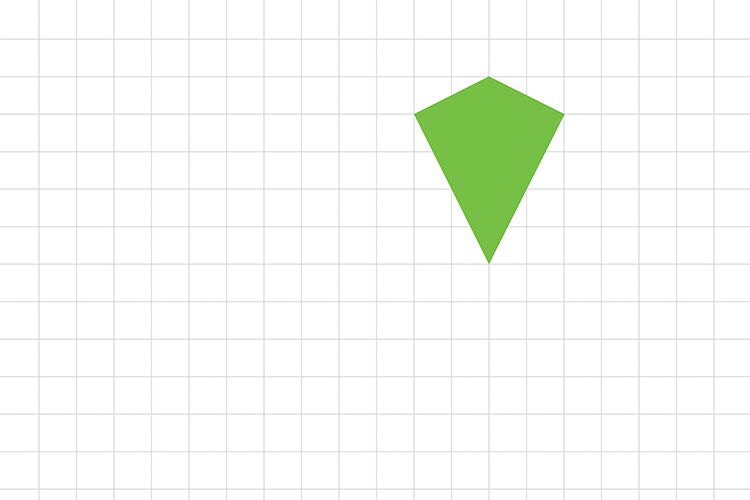
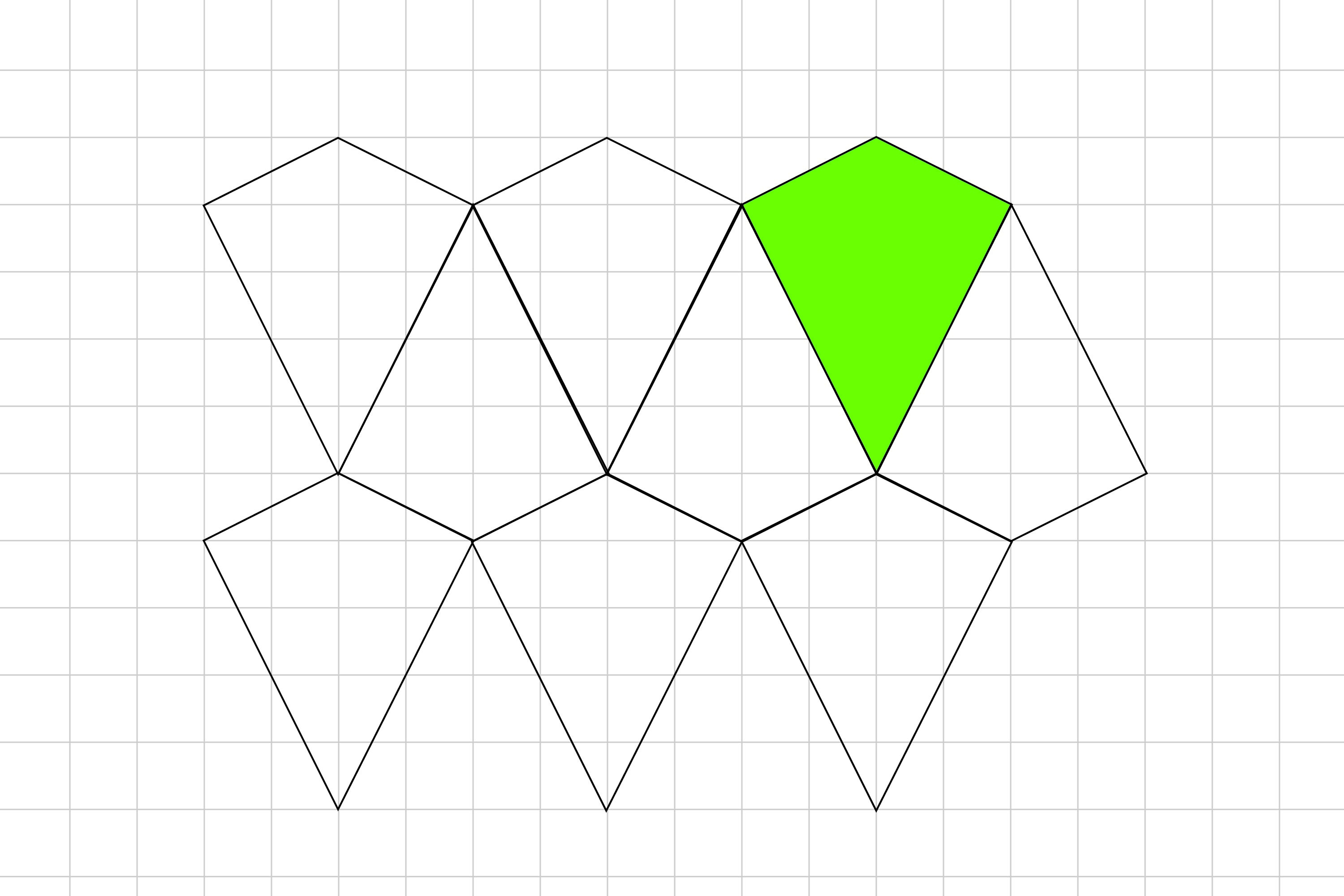
On the graph show this quadrilateral tessellating at least 5 times.
Click on the image below to reveal the answer.
Example 2
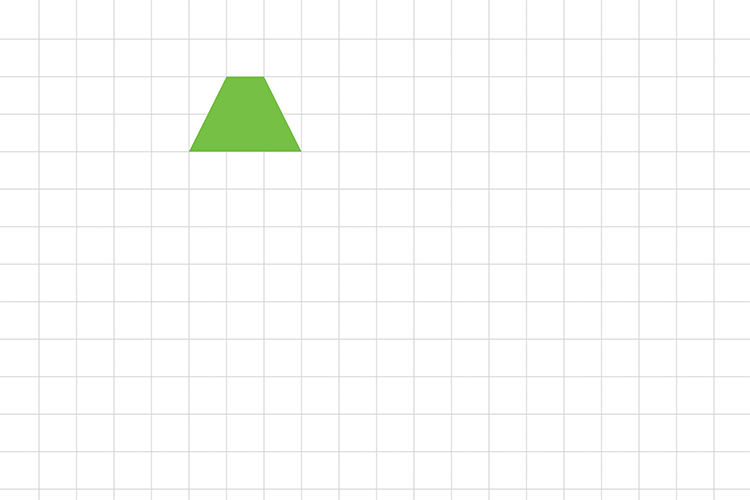
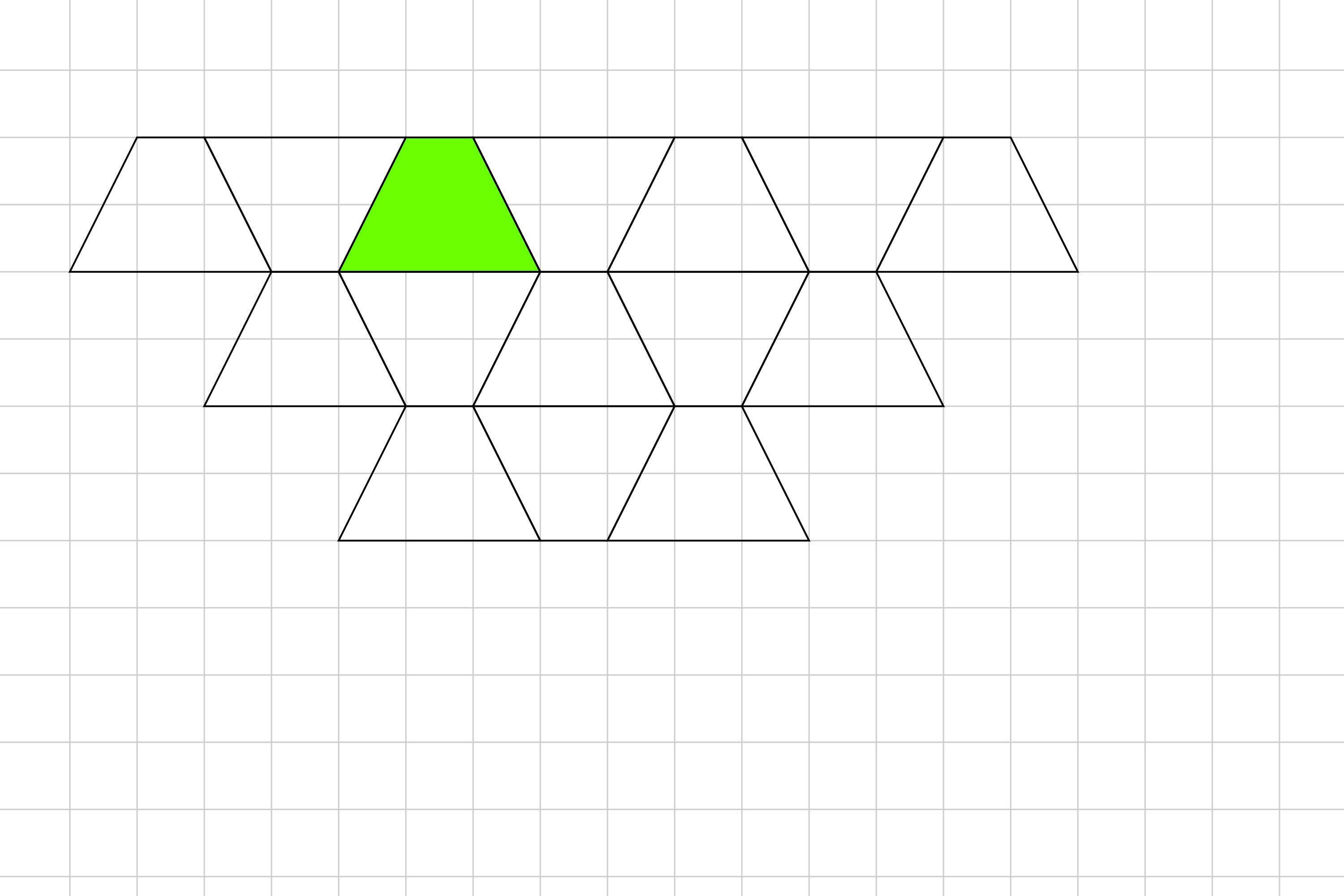
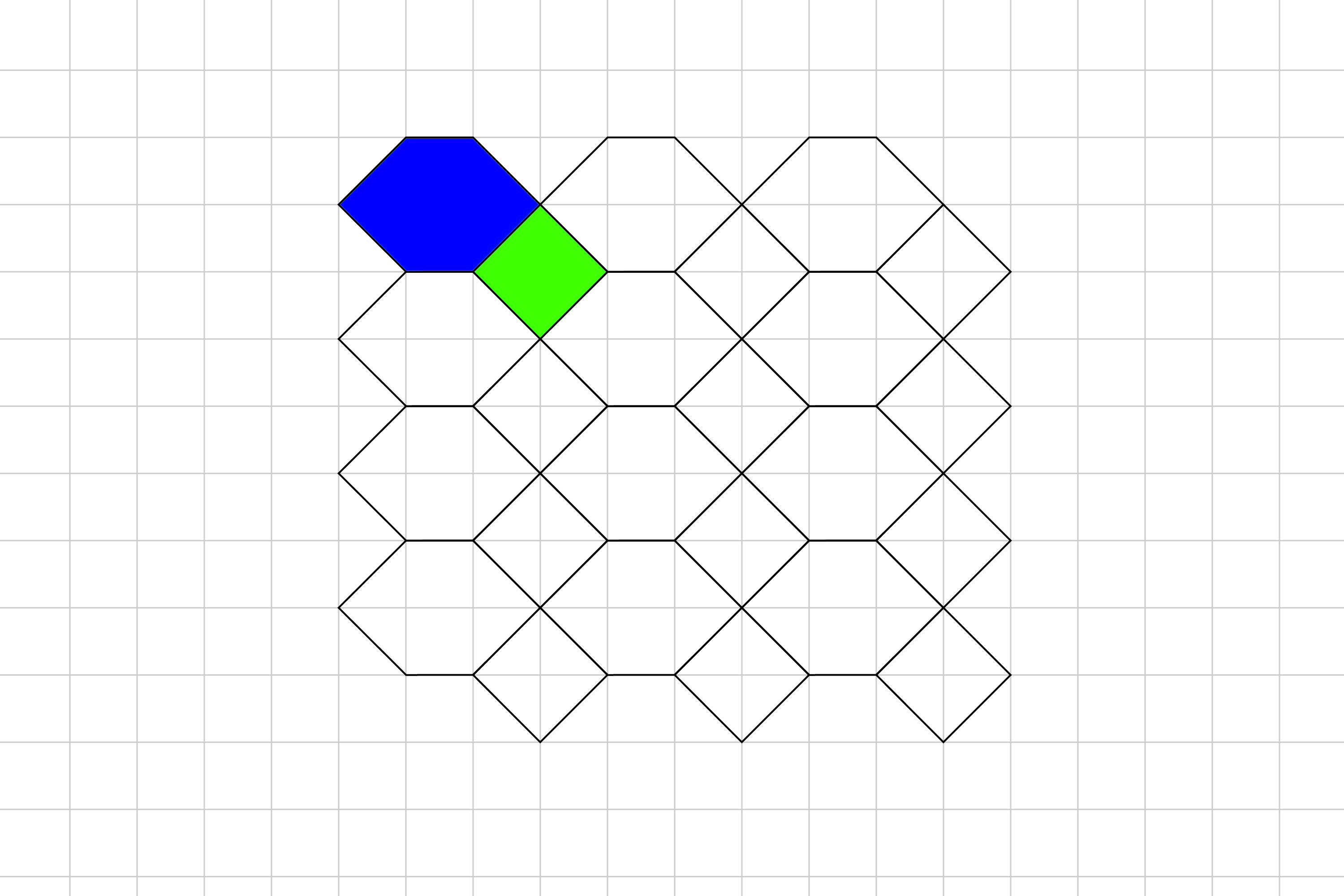
On the grid below draw 7 more quadrilateral tessellations.
Click on the image below to reveal the answer.
Example 3
A bathroom floor needed to be tiled and the owners left two types of tiles. Show in the diagram how the builder will lay the floor.
Click on the image below to reveal the answer.
Example 4
Here is a tessellating pattern made from equilateral triangles.

a) Write down the size of each interior angle in the equilateral triangle.
b) Explain why equilateral triangles tessellate.
Answer:
a) Interior angles of a triangle`=180^@`
As an equilateral triangle has equal length sides all interior angles are equal, so each interior angle `=180/3=60^@`
b) The interior angle of a shape which meets the common vertex must divide into 360 to produce a whole number (integer) in order for it to tessellate. As the interior angles of an equilateral triangle`=60^@`
`360/60=6`
6 is a whole number so equilateral triangles will tessellate.
Example 5
Here is a tessellating pattern made from equilateral triangles and squares.
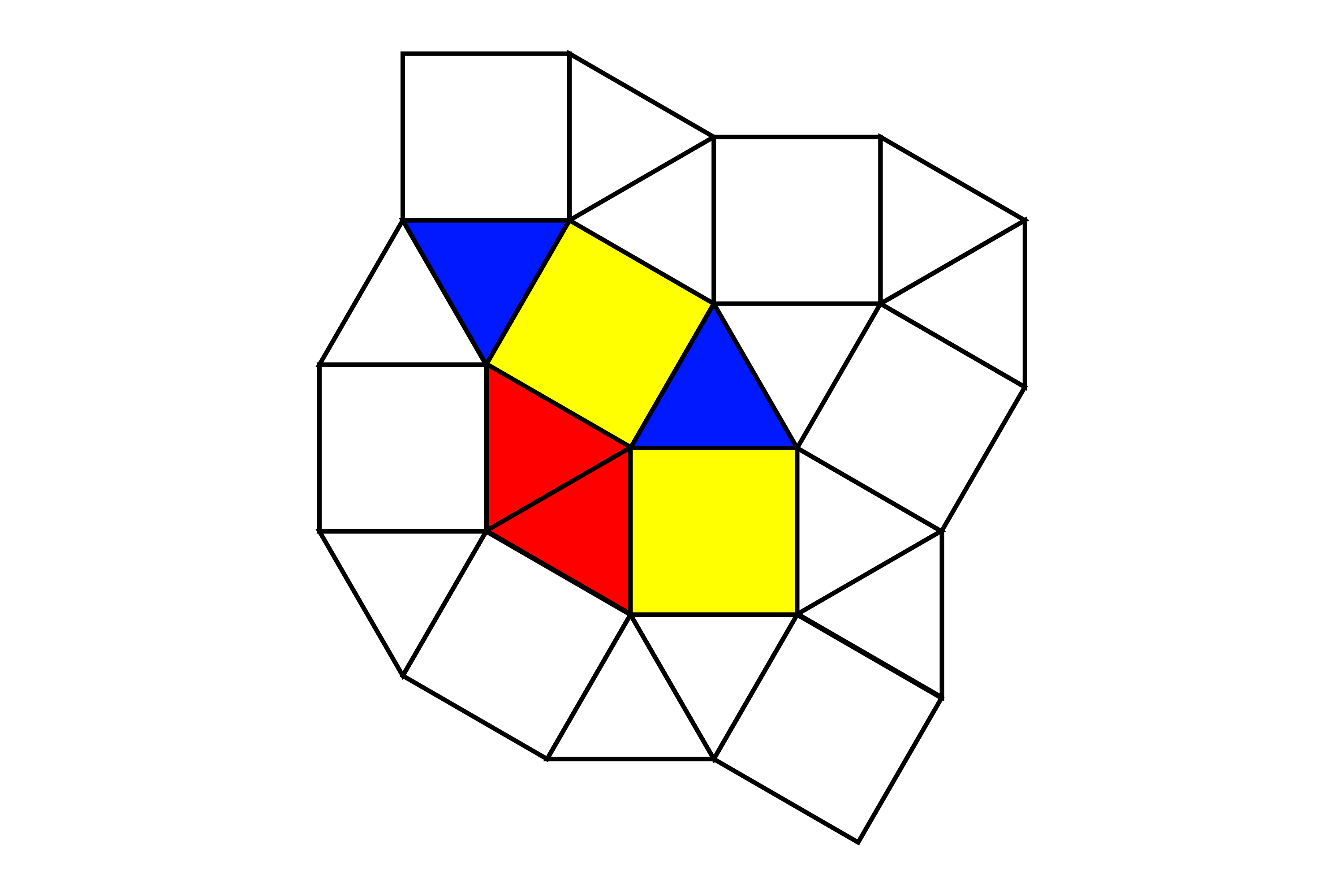
Explain why equilateral triangles and squares can form a pattern that tessellates.
Answer:
For a group of shapes to tessellate the interior angles of the shapes around the common vertex must add up to `360^@`.
In this example the common vertex is at the centre of 2 red equilateral triangles, 2 yellow squares and one blue equilateral triangle. The interior angle of the equilateral triangles `=60^@` and the interior angle of a square `90^@`.
Therefore `90+90+60+60+60=360` so this pattern tessellates.




