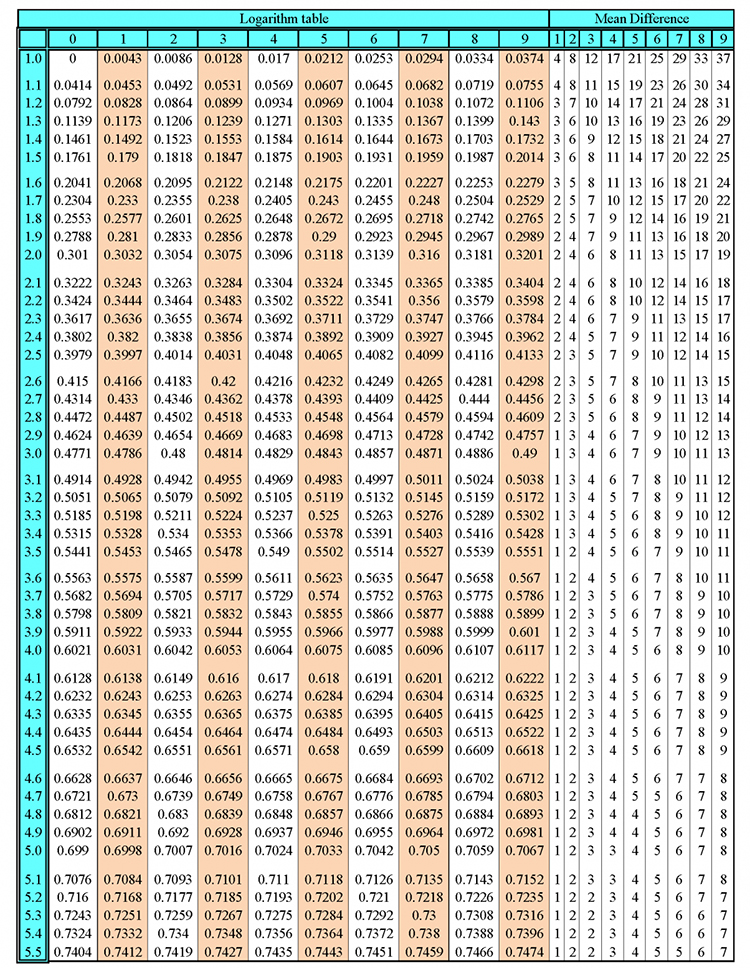
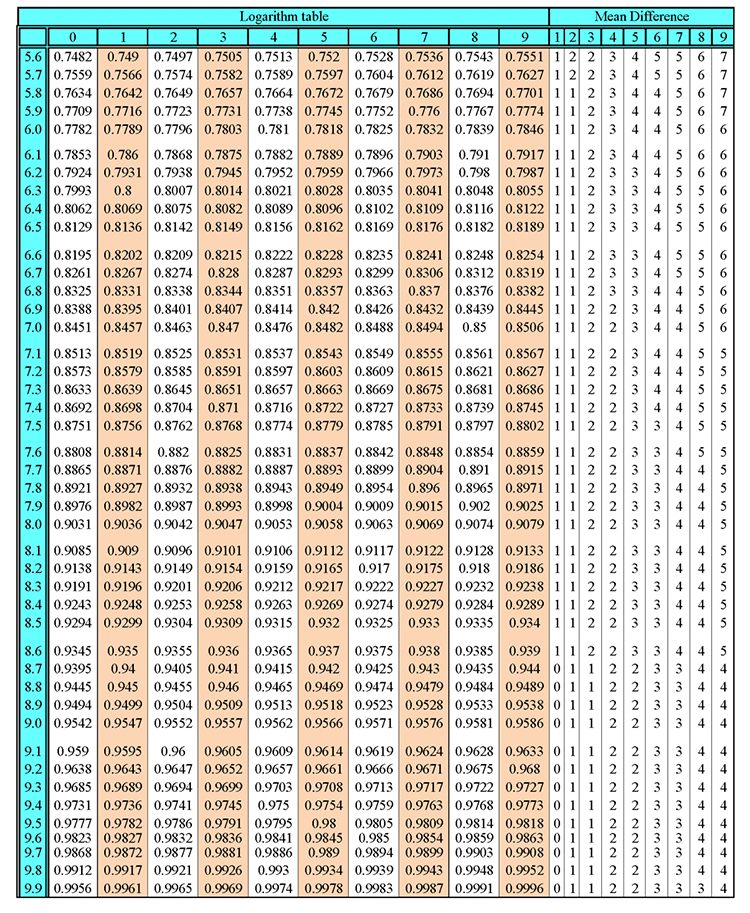
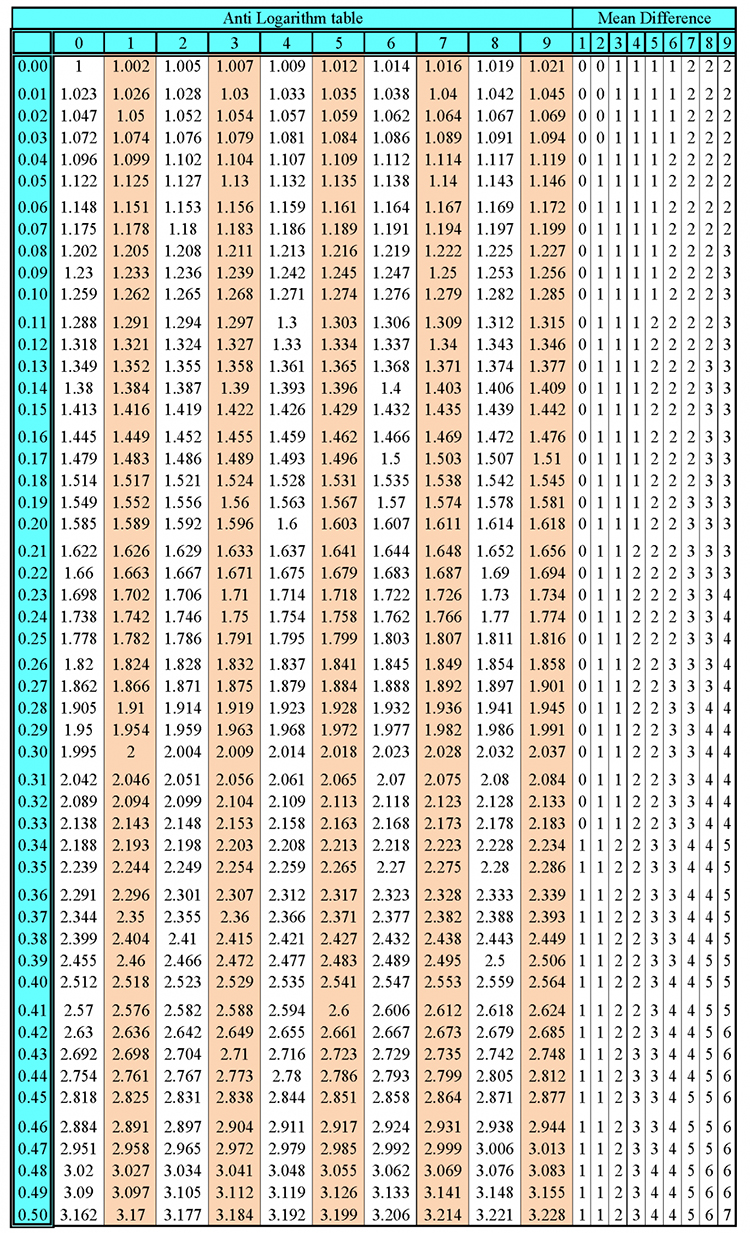
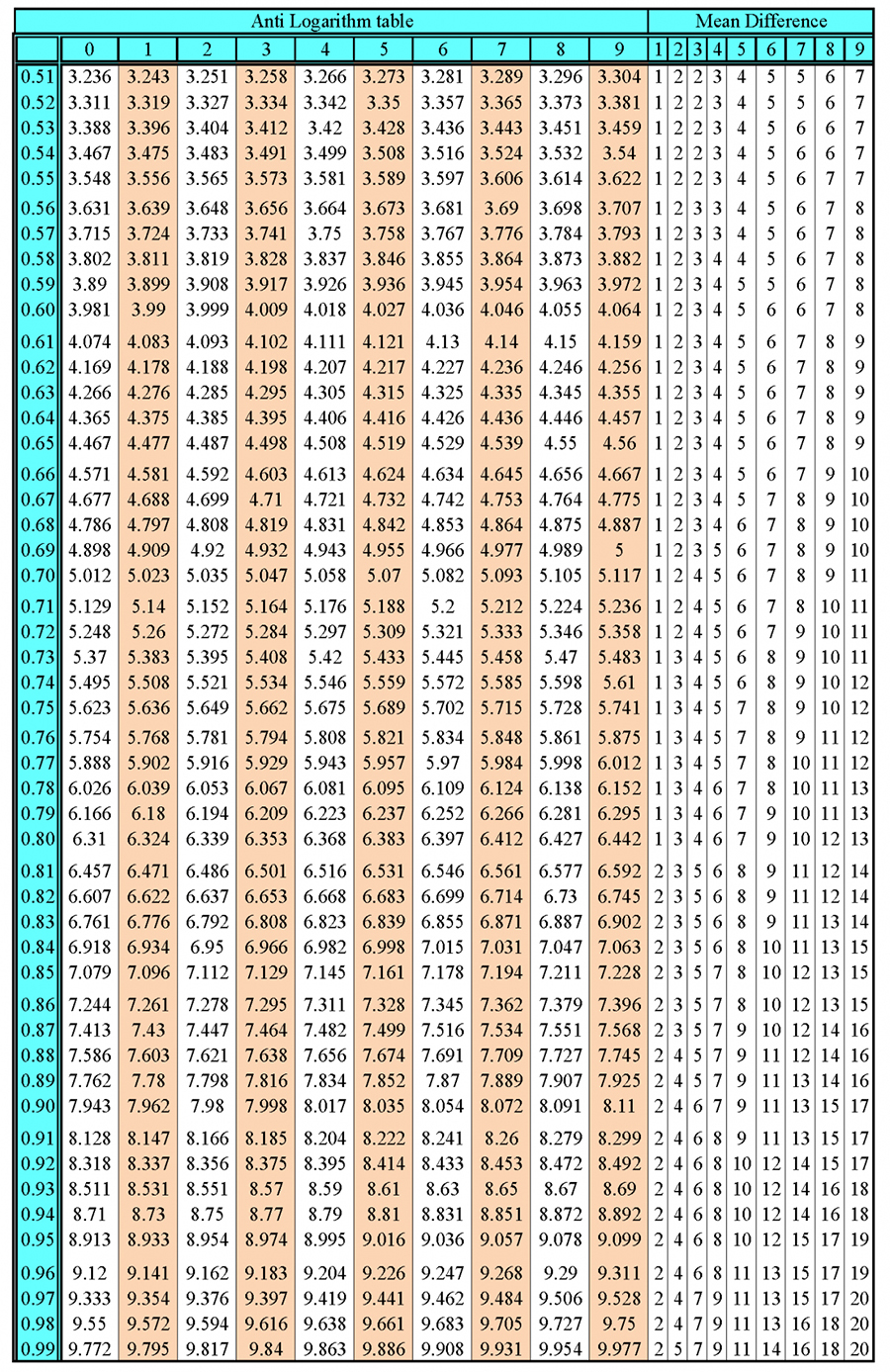
Sum of all internal angles of a polygon

To remember the formula for the sum of all internal angles of a polygon, you should always work out the first three polygons, i.e. triangle, square and pentagon:

Because you know that a triangle's total internal angle is 180° and a square's total internal angle is 360° ask yourself:

How does a triangle (3 sides) get to a total interior angle of 180°.

What is the relationship for number sides to total internal angle?

Ask yourself how does a square (4 sides) get to a total interior angle of 360°

What is the relationship for number sides to total internal angle?

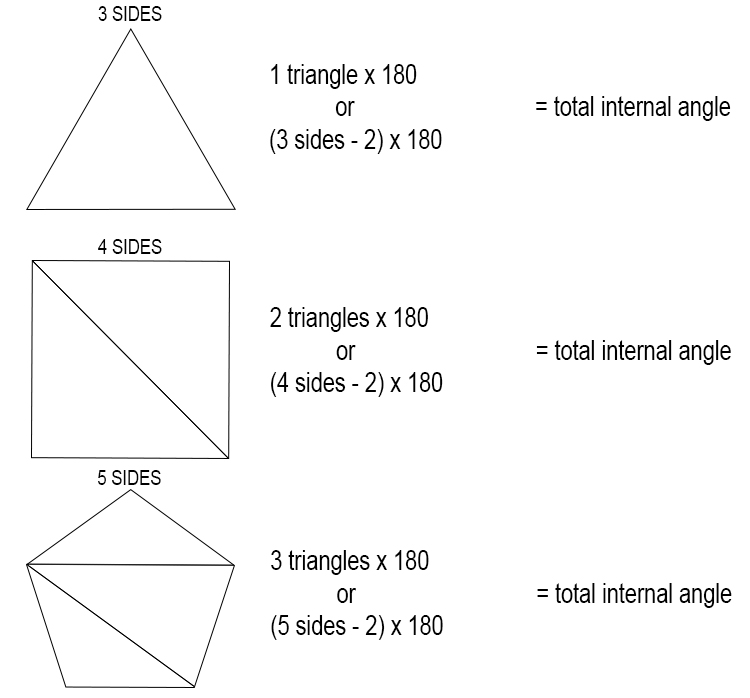
To remember the formula for the sum of all internal angles of a polygon, you should always work out the first three polygons, i.e triangle, square and pentagon.

Therefore, the sum of all the internal angles

`=(Number of sides -2)times180`

which is often shown as

`=(n-2)times180`

where n is the number of sides.