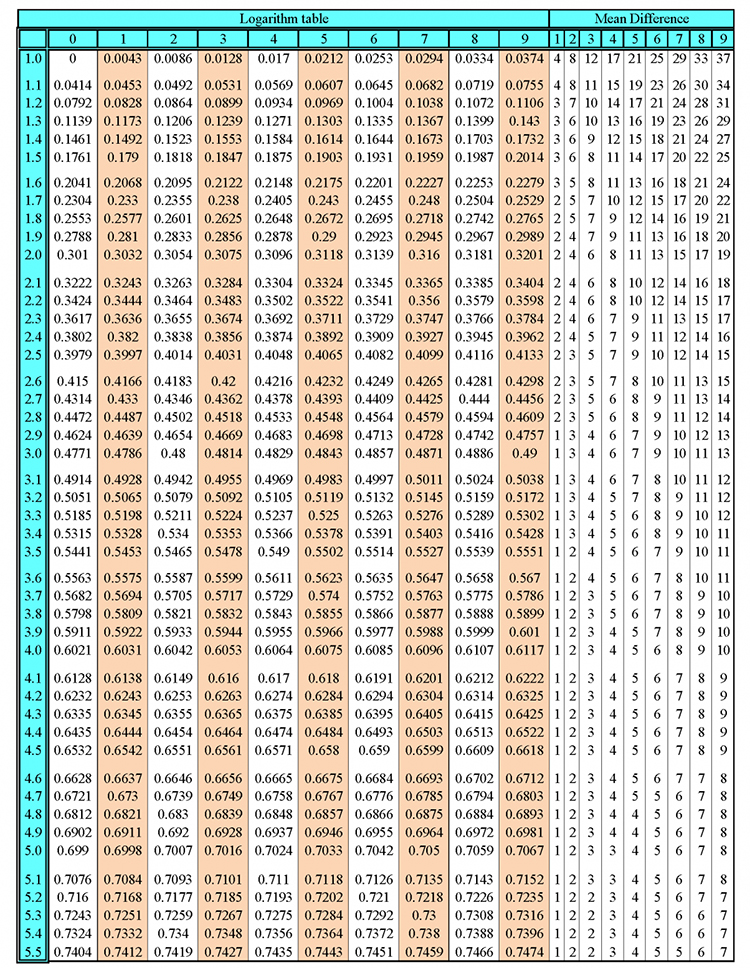
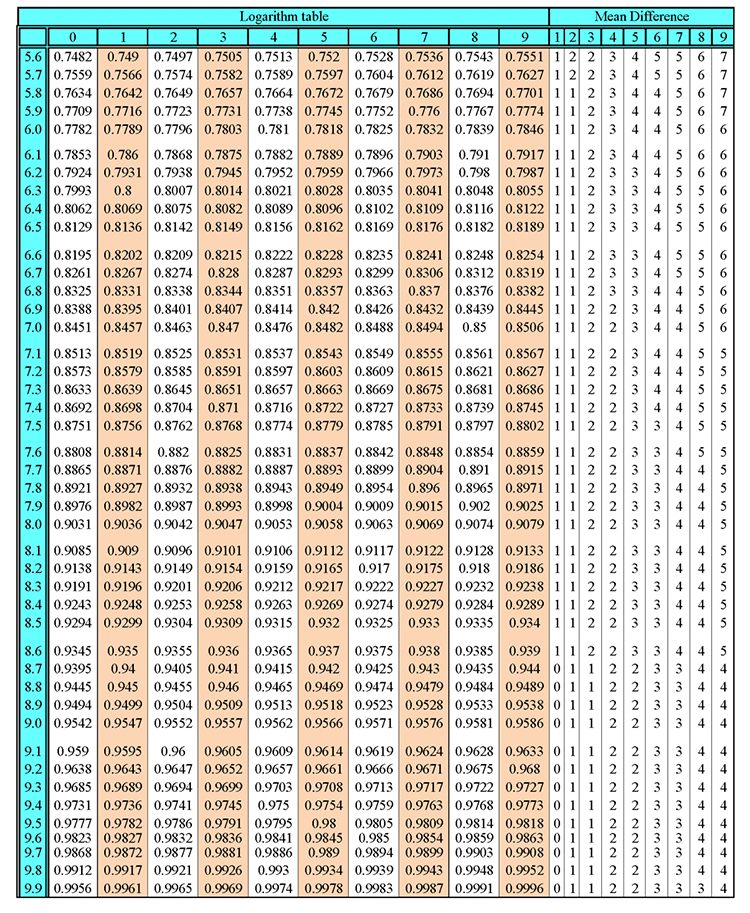
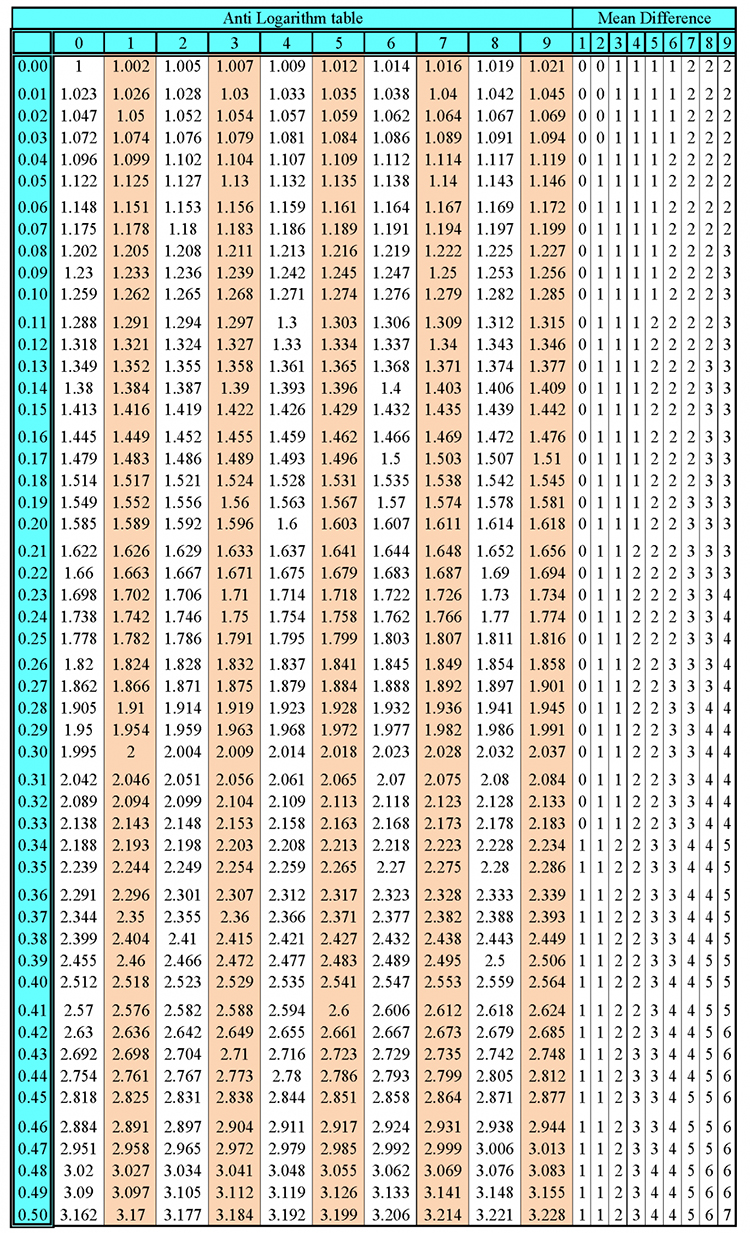
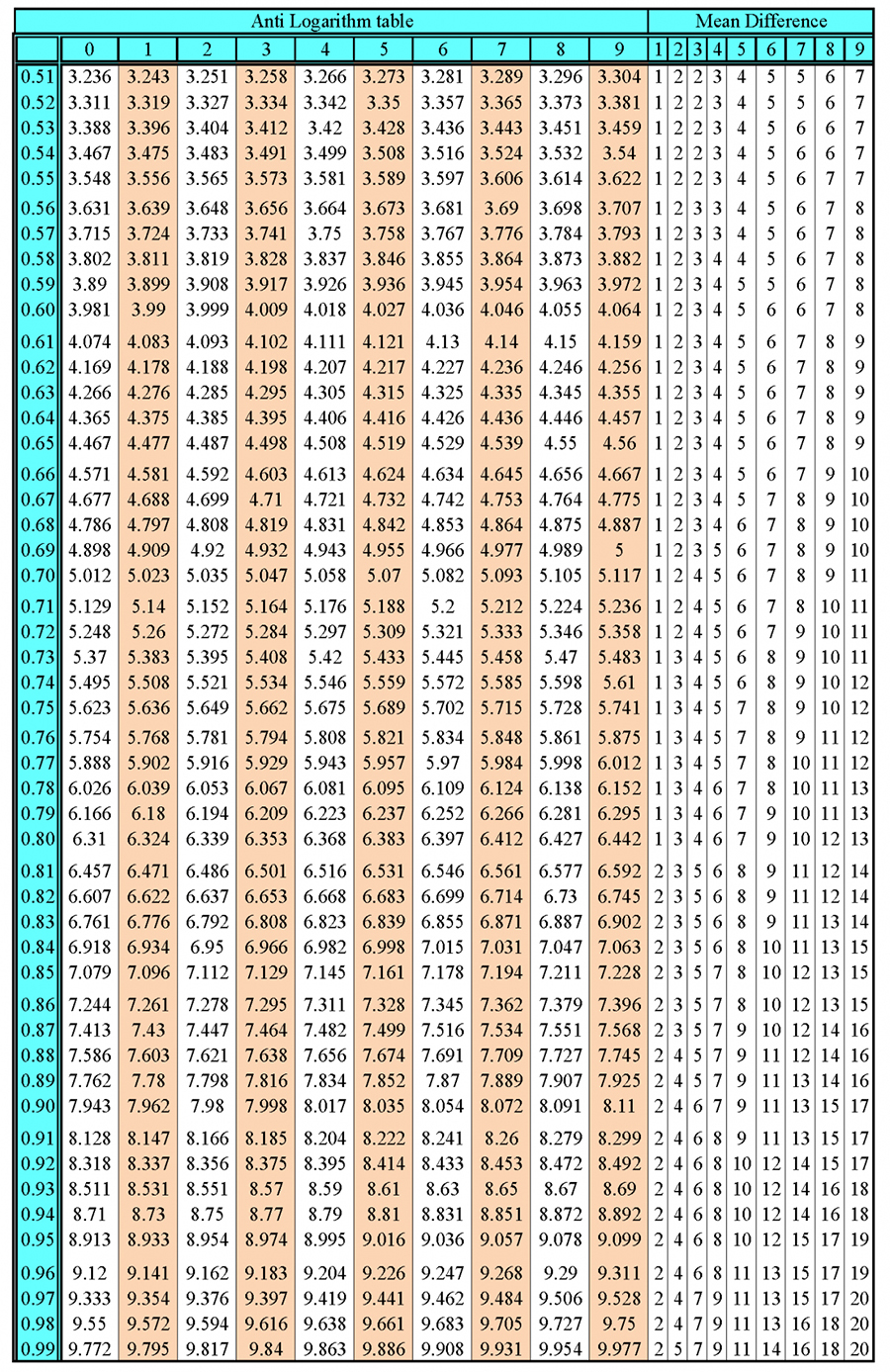
The total interior angles of an octagon = 1080°
Each time we add a side (triangle to square, square to pentagon, pentagon to hexagon) we add another 180°.
Triangle to octagon
|
Triangle |
|
Square |
|
Pentagon |
|
Hexagon |
|
Heptagon |
|
Octagon |
|
|
|
`180°` |
`+` |
`180°` |
`+` |
`180°` |
`+` |
`180°` |
`+` |
`180°` |
`+` |
`180°` |
`=` |
`1080°` |
The total internal angles of a heptagon = 1080°
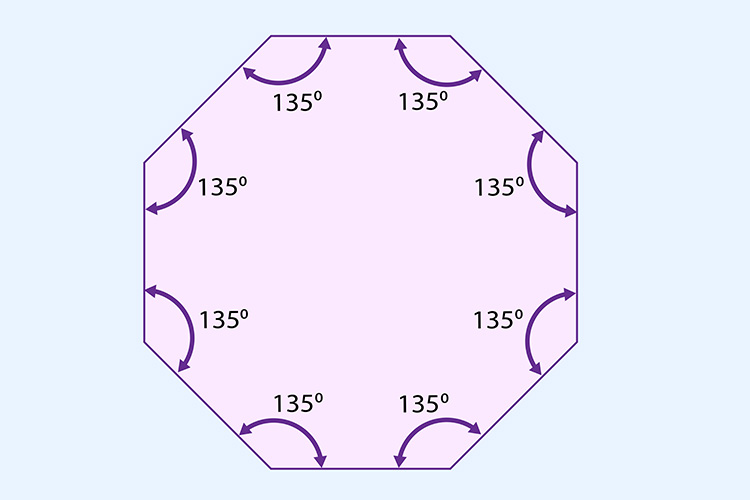
Now, divide the total internal angle by the number of corners.
i.e. divide 1080° by 8.
`1080^circ/8=135^circ`
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
|
|
`135°` |
`+` |
`135°` |
`+` |
`135°` |
`+` |
`135°` |
`+` |
`135°` |
`+` |
`135°` |
`+` |
`135°` |
`+` |
`135°` |
`=` |
`1080°` |