Resizing examples

Example 1

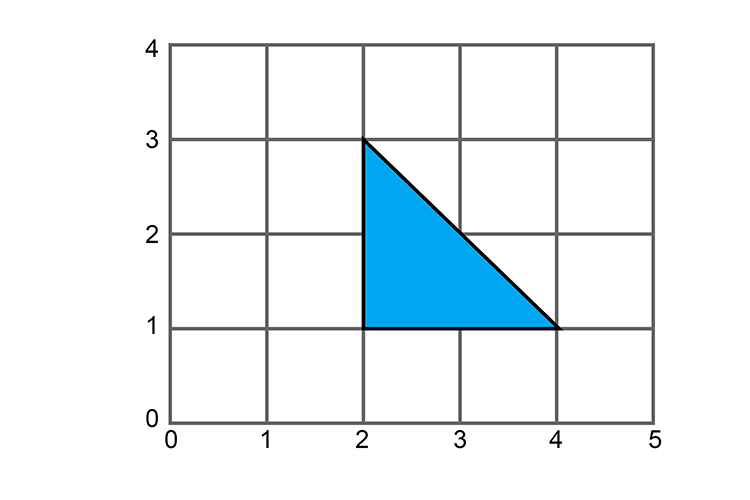
Enlarge the following shape by a scale of 3 from the graph origin.

Resize this shape to scale 3

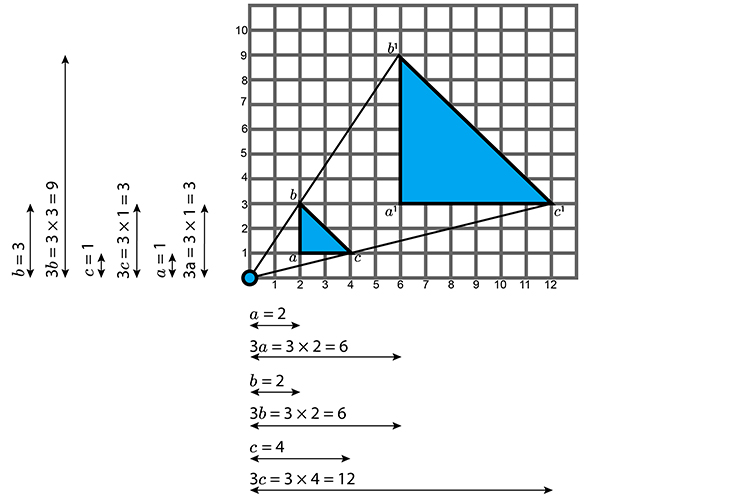
Explaining the resizing

Example 2

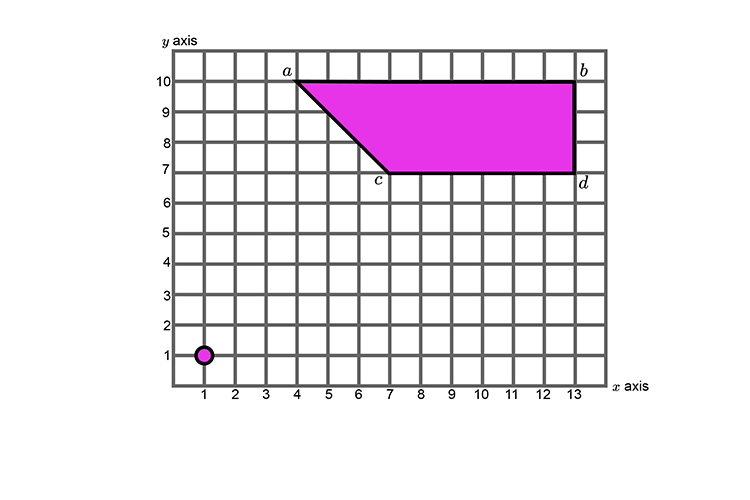
Resize the following shape by a `1/3` from the centre co-ordinates (1,1).

Resize by 1 third

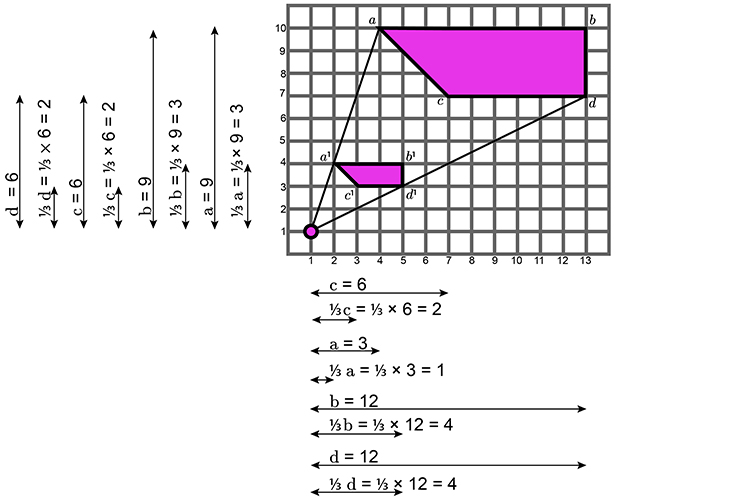
Explaining the resizing

Example 3

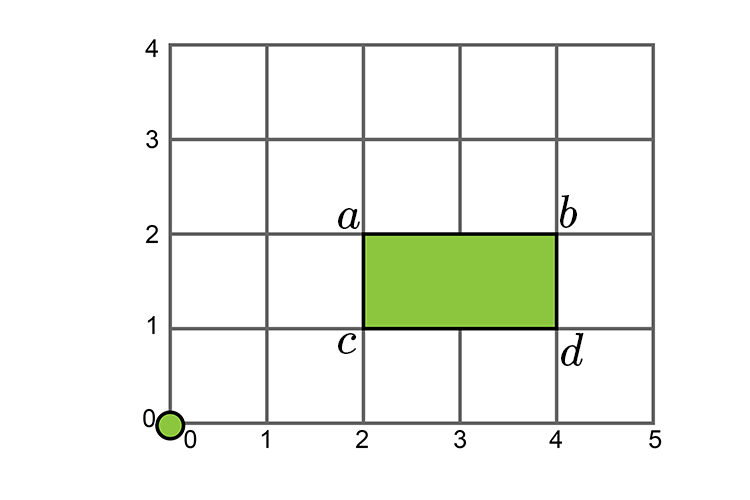
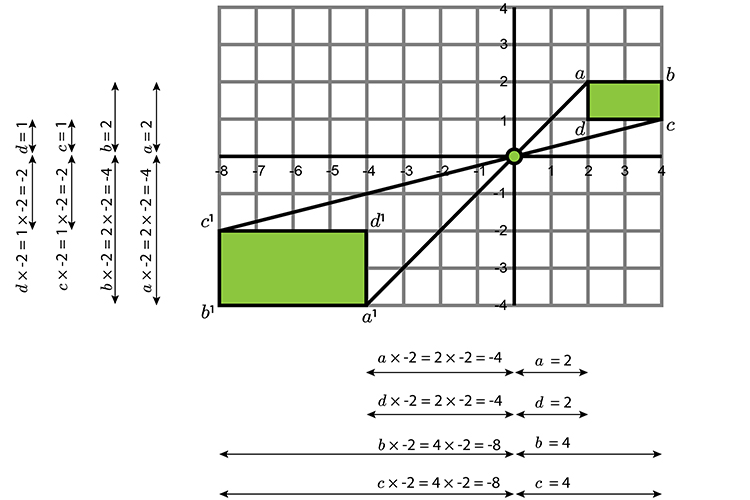
Resize the following rectangle by a factor of `-2` with the centre at the origin (of the graph).

Resize by minus 2

Explaining the resizing

Example 4

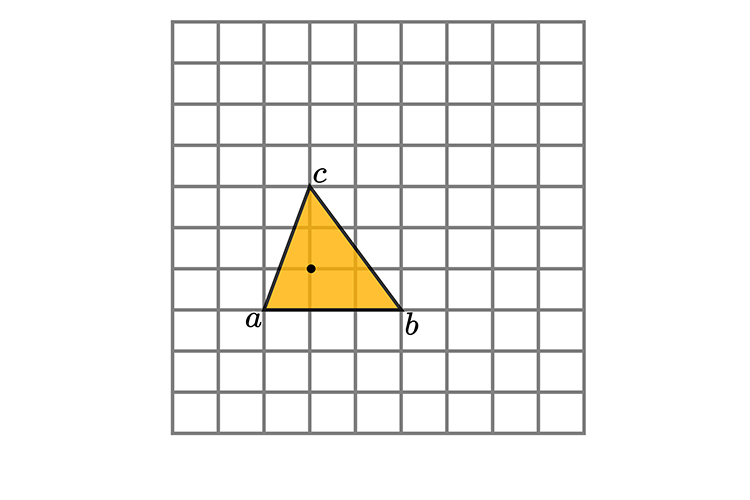
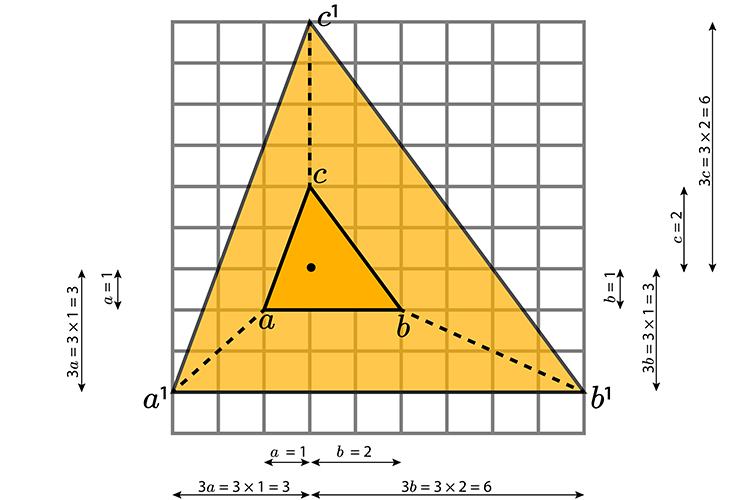
Enlarge the following triangle by a scale of 3 from the graph origin (0).

Resize this image by scale 3 origin means movement so resize but don’t move

Explaining the resizing and positioning

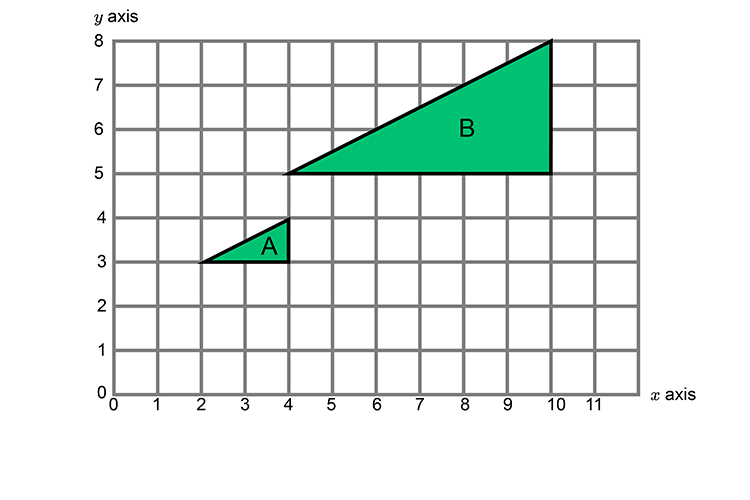
Example 5

Describe fully the transformation which maps triangle A onto Triangle B.

Describe this transformation of triangle A to triangle B

The first stage is to find the origin which you can achieve by joining the respective corners with a line and extending them.

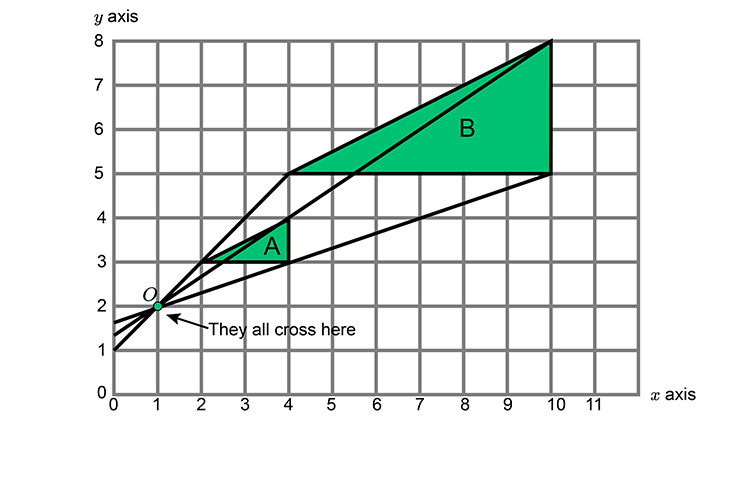
Find the intersection of the corners first and mark it

The extended lines all cross at point O which must therefore be the CENTRE point.

We must now work out the scale.

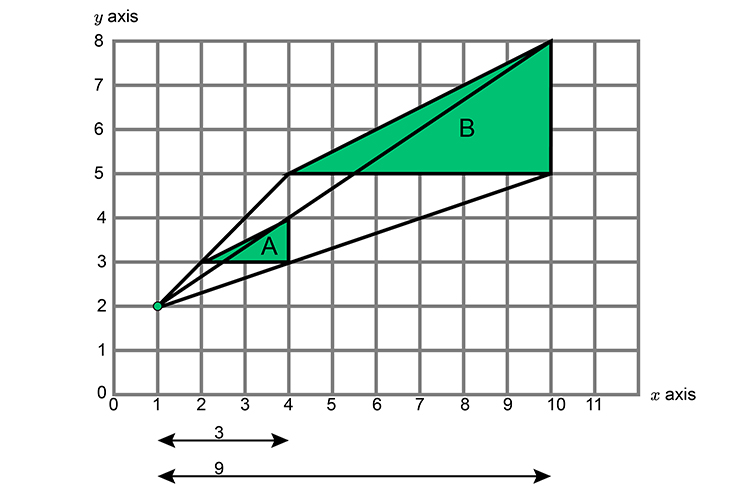
Measure the distance of both shapes from the intersection which gives you scale

Take any point and on one side alone work out the change in scale.

`3` becomes `9`

`3timesx=9`

`x=9/3`

`x=3`

Check

`3times3=9`

So the answer is: The single transformation which maps triangle A onto triangle B is an enlargement with centre of coordinate (1,2) and scale of `+3`.