Rotation - using logic

Determining new coordinates using logic

You can determine the new coordinates of an object using:

Rotation & the "L" shape

It works by joining the origin with the point to be rotated with an "L" shape.

Example 1

Rotate the following object clockwise 90° from the centre (1,3).

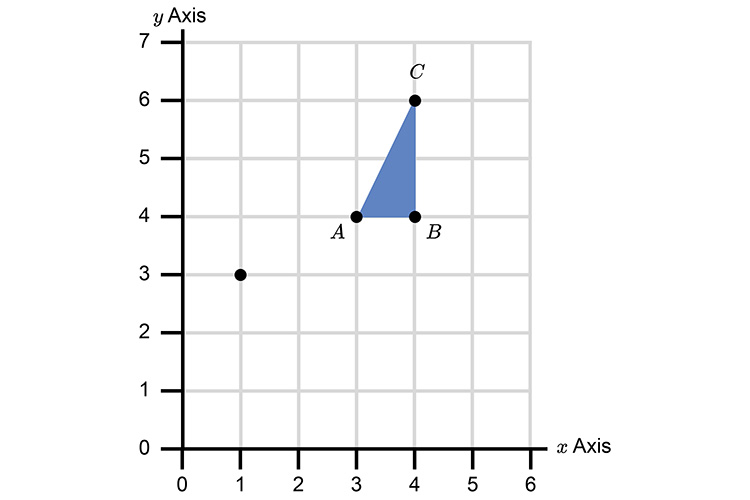
Rotate this triangle 90 degrees clockwise

Join the origin to A with an L.

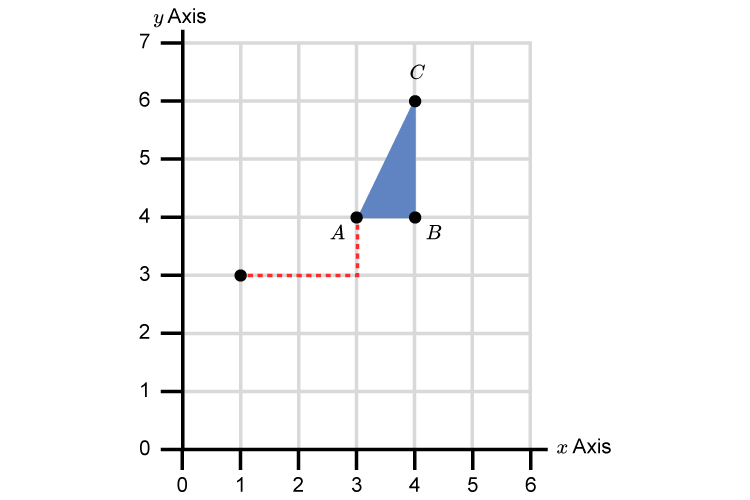
Draw from the pivot point to the closest corner of the shape

Now we are only dealing with right angles which makes this very easy when we want to turn a point through 90° clockwise.

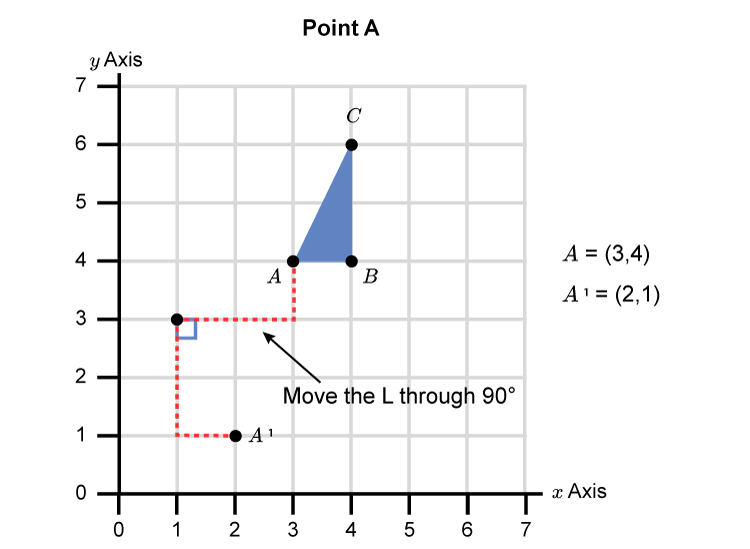
Rotate the new lines by 90 degrees using the pivot so the point has a right angle on both lines

Do the same as corner A with corner B

Do the same as corner A with corner C

This gives a final graph as:

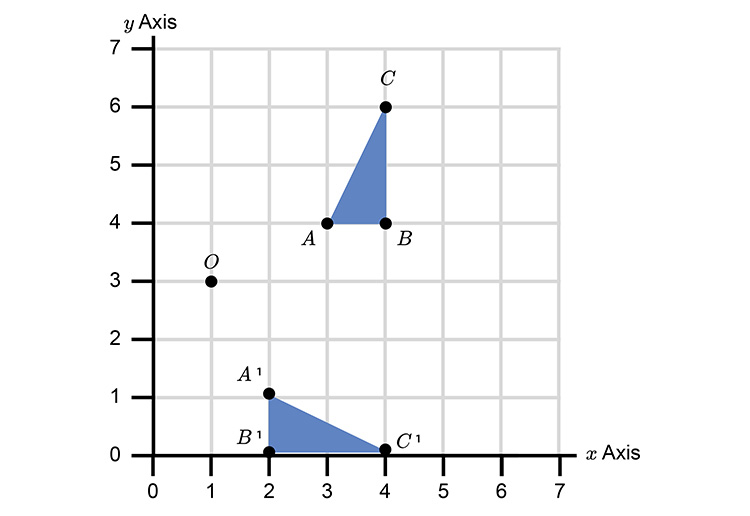
Draw the rotated shapes by joining the new corners

`A, B, C` has been rotated clockwise 90° from centre (1,3) to give the new triangle `A^1, B^1, C^1`.

Example 2

Rotate the following triangle 180° about the origin (0,0).

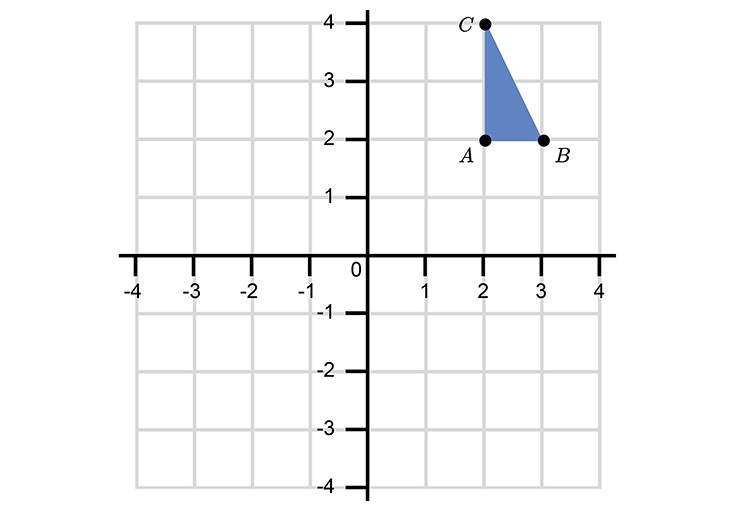
Rotate the triangle through 180 degrees

Rotate point `A` 180° using the L shape.

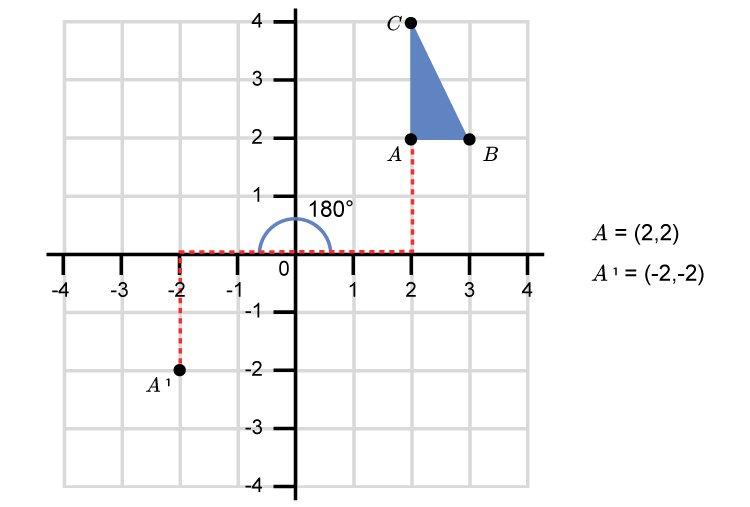
Rotate corner A using the L method

Rotate point `B` 180° using the L shape.

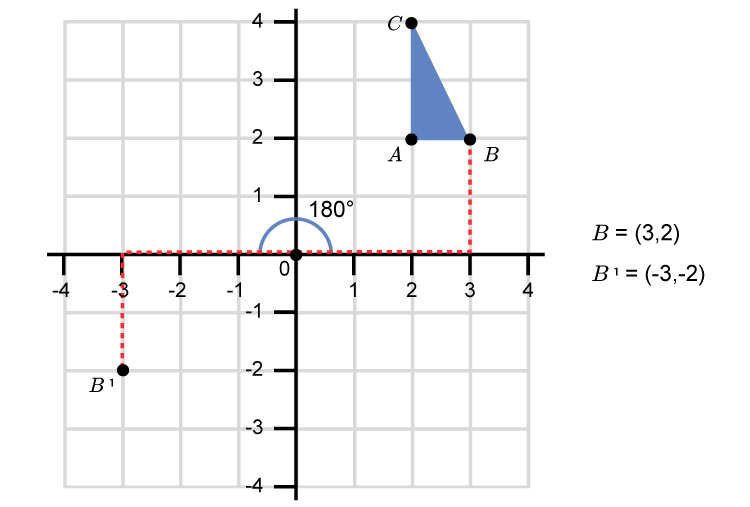
Rotate corner B using the L method

Rotate point `C` 180° using the L shape.

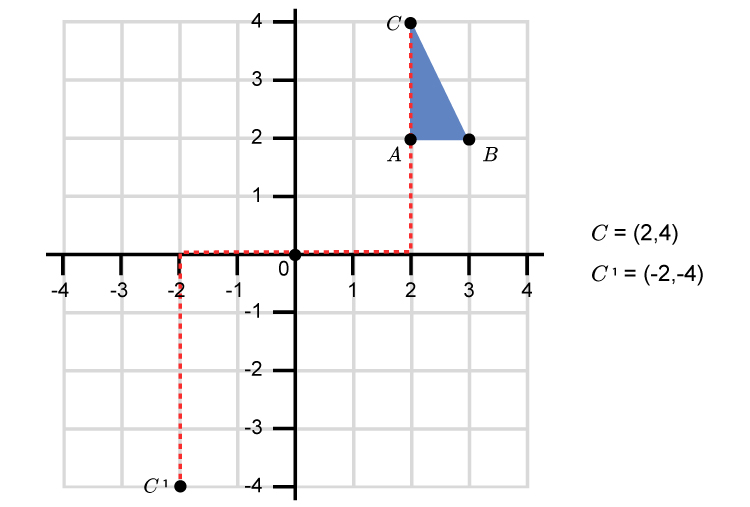
Rotate corner C using the L method

This gives a final graph as:

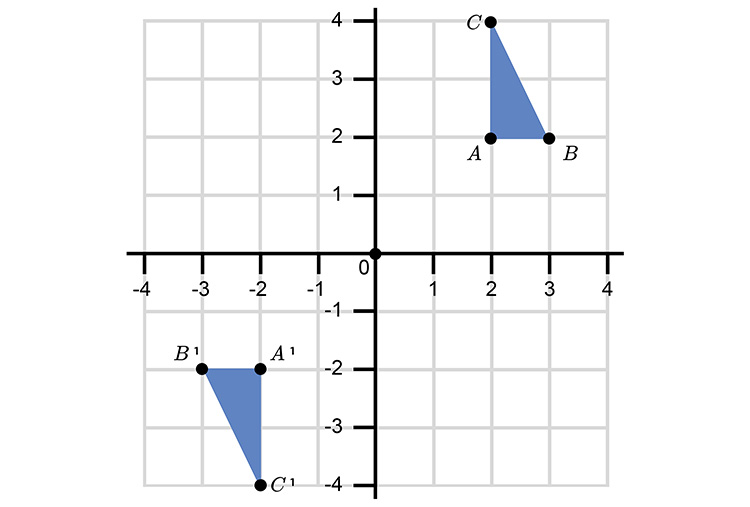
This is the final graph

`A, B, C` has been rotated 180° from the centre (0,0) to give the new triangle `A^1, B^1, C^1`.

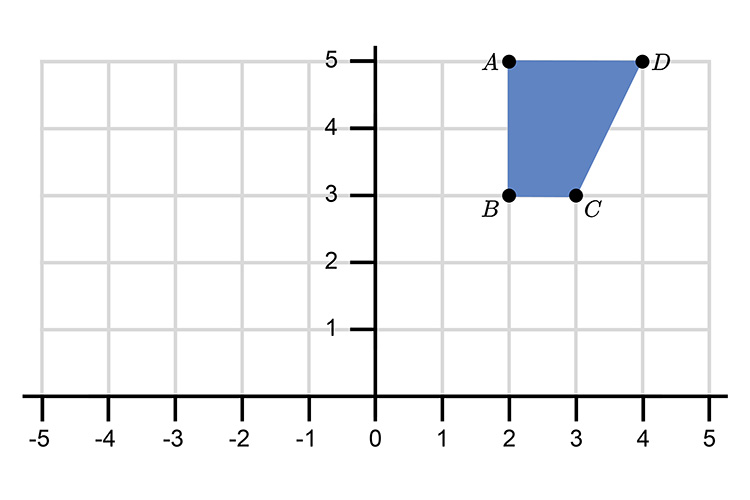
Example 3

Rotate the following shape 90° anticlockwise about grid point (1,1).

Rotate this shape anticlockwise by 90 degrees

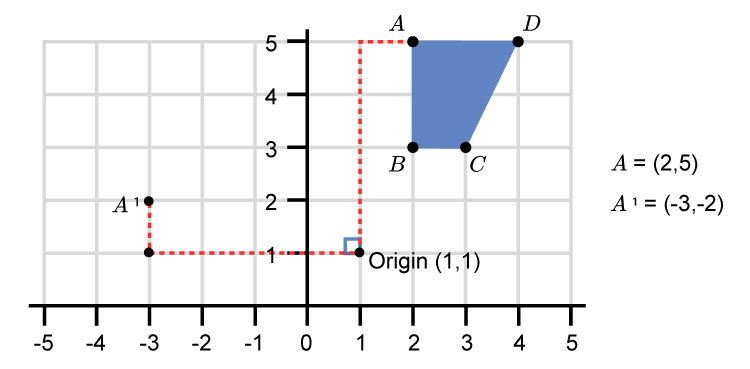
Rotate point `A` 90° using the L shape.

Rotate corner A using the L method

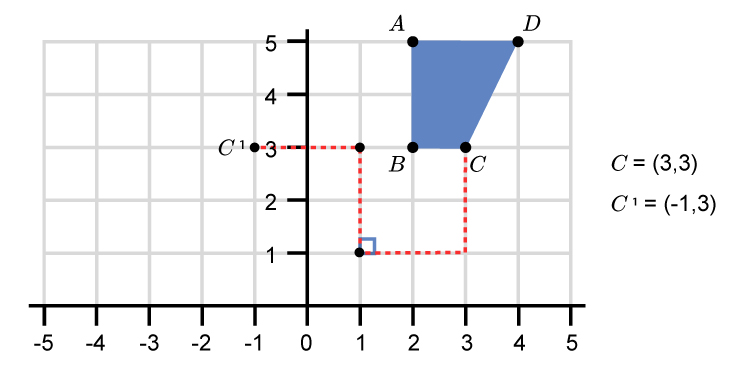
Rotate point `B` 90° using the L shape.

Rotate corner B using the L method

Rotate point `C` 90° using the L shape.

Rotate corner C using the L method

Rotate point `D` 90° using the L shape.

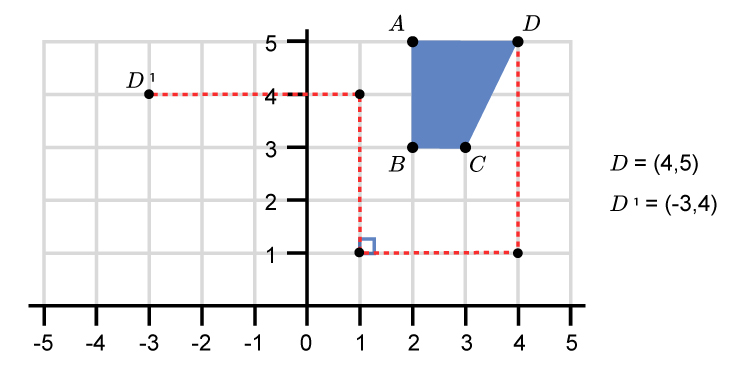
Rotate corner D using the L method

This gives a final graph as:

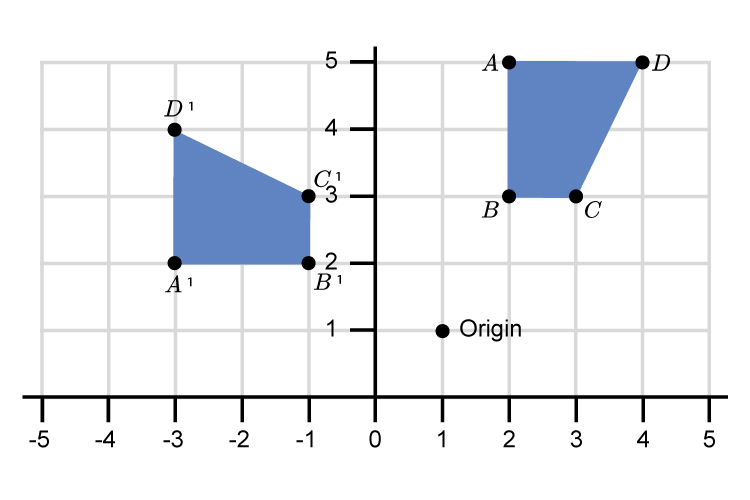
This gives the final graph with origin in place

`A,B,C,D` has been rotated 90° anti clockwise about centre (1,1) to give `A^1,B^1,C^1,D^1`.