Rotation

Determining new coordinates using a picture

You can determine the new coordinates of an object

Only if
the origin is (0,0)
and only if
you rotate `90^@`, `180^@` or `270^@`

Remember this picture:

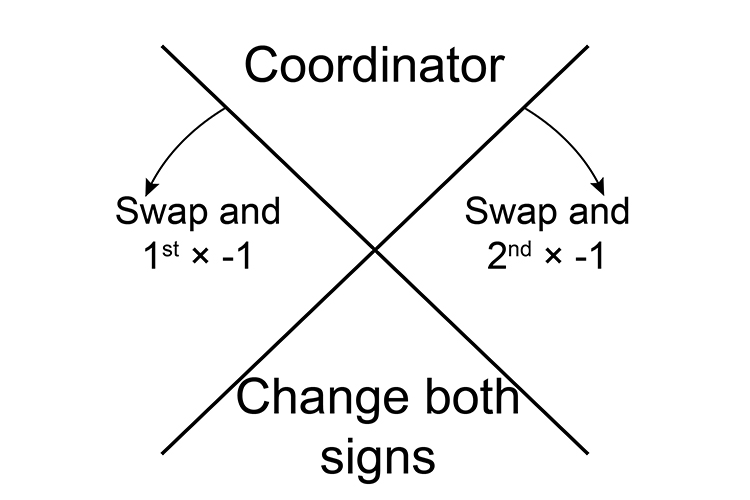
The above says:

1. Move clockwise 90°
   1. Swap the coordinates
   2. Then multiply the second coordinate by `-1`
2. Move anticlockwise 90°
   1. Swap the coordinates
   2. Then multiply the first coordinate by `-1`
3. Move 180°
   1. Just change both signs

Example 1

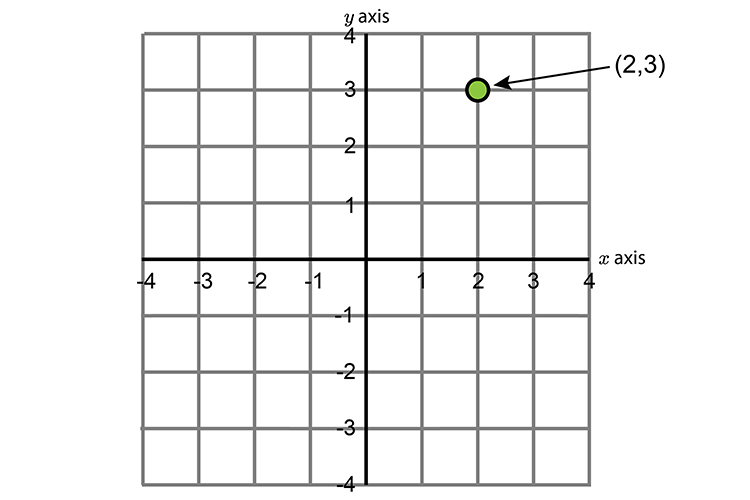
With origin (0,0) rotate the point (2,3) by

1. Clockwise 90°
2. Anticlockwise 90°
3. Through 180°

and plot your answers

Answer:

To remember how to do this write out the following:

1. Clockwise 90°
   1. Swap the coordinates:
              The coordinates are`(2,3)`
              swap and they become `(3,2)`
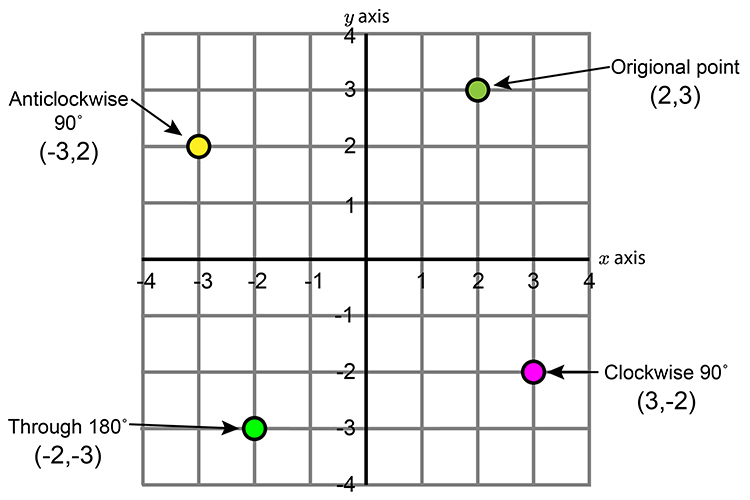
   2. Then multiply the second coordinate by `-1`:
              `(3,2)`  becomes `(3,-2)`
2. Anticlockwise 90°
   1. Swap the coordinates:
               The coordinates are`(2,3)` 
               swap and they become `(3,2)`
   2. Then multiply the first coordinate by `-1`:
              `(3,2)`  becomes `(-3,2)`
3. Through 180°
   1. Just change the signs:
               The coordinates are `(2,3)` 
               `(2,3)`  becomes `(-2,-3)`

Plot the answer:

Example 2

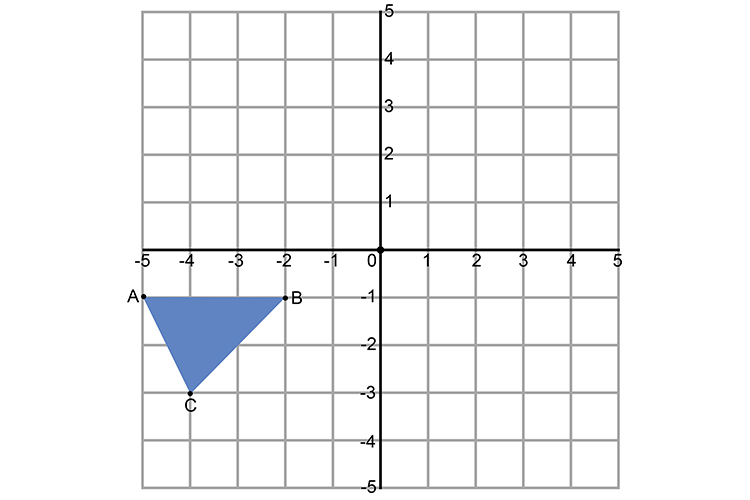
Rotate The object below anticlockwise by 90° with origin (0,0).

So we would use:    SWAP and 1st number `times-1`

Point A `=(-5,-1)`  becomes `(-1(times-1),-5)=(1,-5)`

Point B `=(-2,-1)`  becomes `(-1(times-1),-2)=(1,-2)`

Point C `=(-4,-3)`  becomes `(-3(times-1),-4)=(3,-4)`

The graph becomes:

Does this look correct? YES IT DOES

Example 3

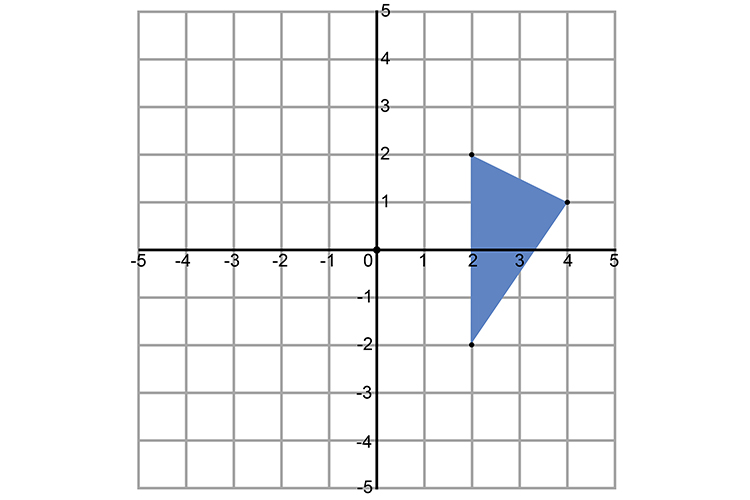
Rotate the triangle below anticlockwise by 90° with origin (0,0).

Use

We would use:    SWAP and 1st number `times-1`

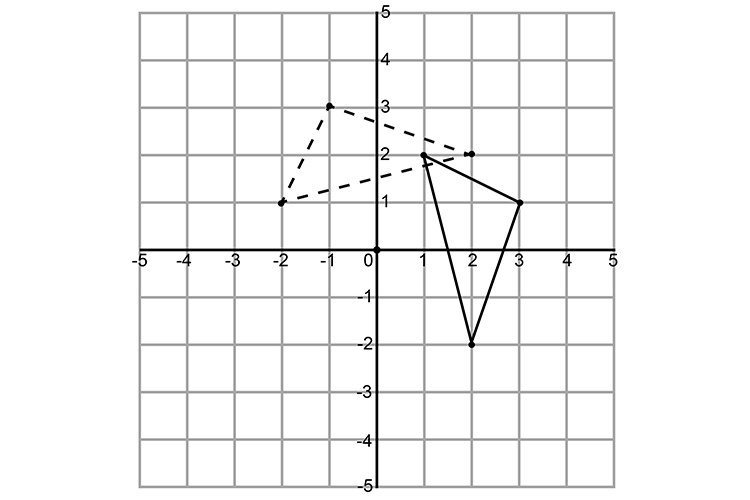
`A=(1,2)`  becomes `(2times(-1),1)=(-2,1)`

`B=(3,1)`  becomes `(1times(-1),3)=(-1,3)`

`C=(2,-2)`  becomes `(-2times(-1),2)=(2,2)`

The graph becomes:

Example 4

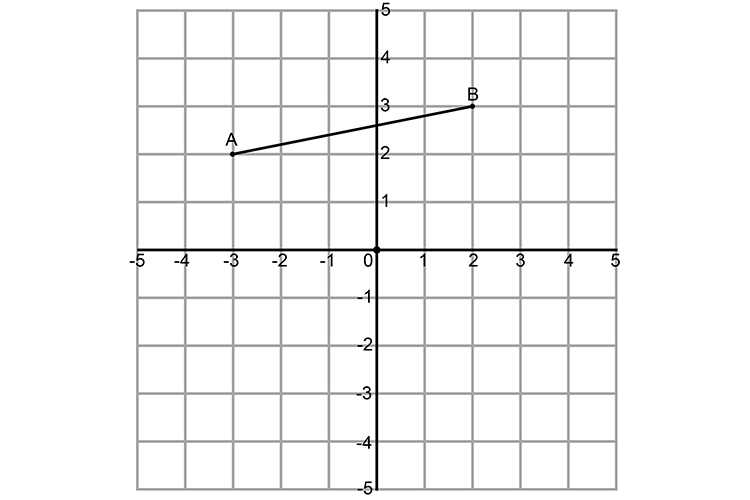
Rotate the line below by 180° with the origin at (0,0).

Use

We would use:    Change both signs

So if `A=(-3,2)`  and `B=(2,3)`

The new coordinates would be: 

`A^1=(3,-2)`  and `B^1=(-2,-3)`

Plot the results:

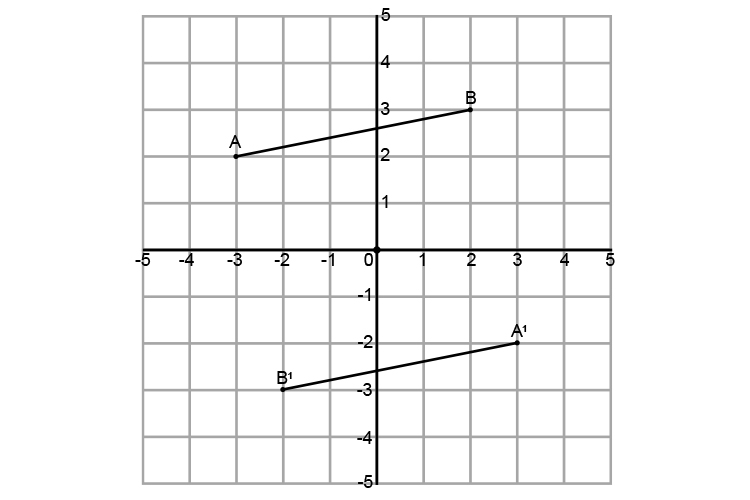
As a check you could run `A`  and `B`  through the origin and see if they hit`A^1`  and `B^1`  at the same distance from the origin:

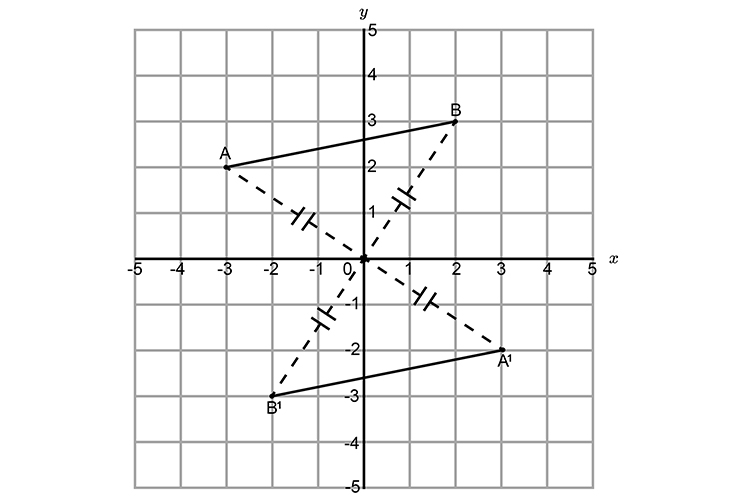
This is correct.