Resizing - Enlargement, contraction

In order to describe an enlargement or contraction of an object in maths you have to find its centre and the scale of reduction or enlargement.

Centre and scale

Memory aid to help you remember you have to find the centre and scale first

What an enlargement and she's covered in scales get her to the health CENTRE.

Resizing means the shape gets bigger or smaller

Resizing means the shape gets bigger or smaller without changing shape

The shape is similar i.e. all the angles and proportions stay the same.

They call this many names;

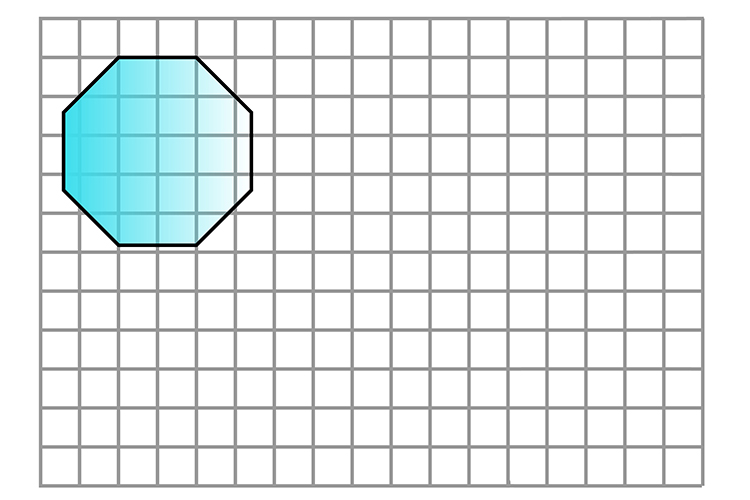
If you are just asked to enlarge a shape on a graph such as

Example

Enlarge the following shape by a scale of 2 or factor of 2.

To resize the shape you first have to define how big

Then your new shape will be:

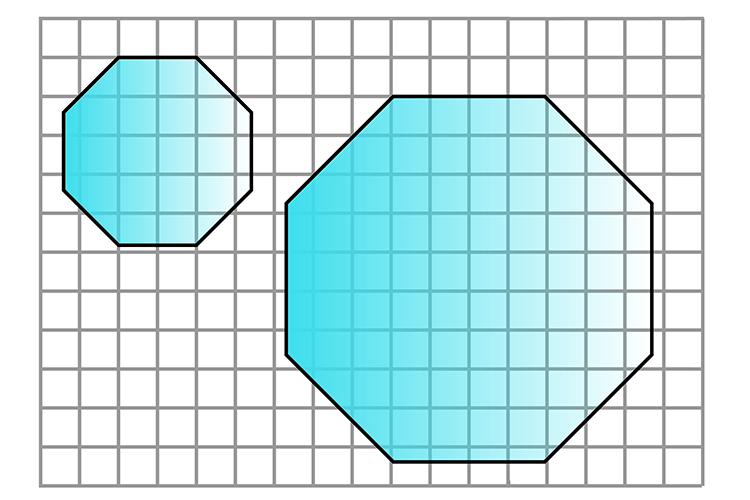
The new shape should be doubled so it is twice as big but doesn’t change shape

Twice as big.

The position of the enlarged shape hasn't been mentioned.

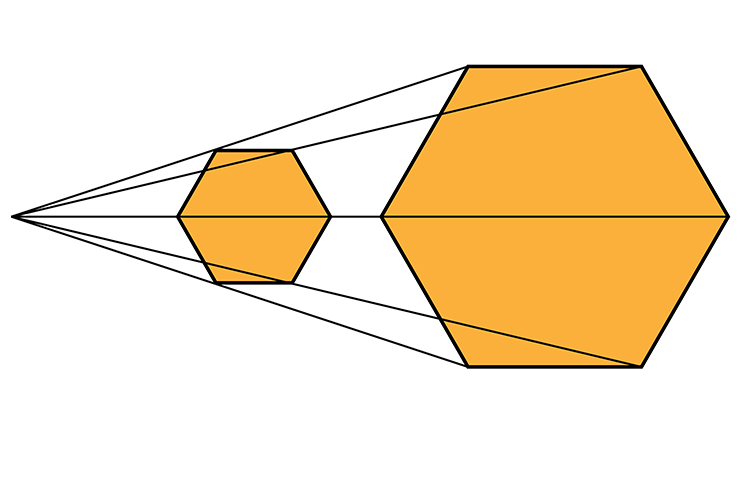
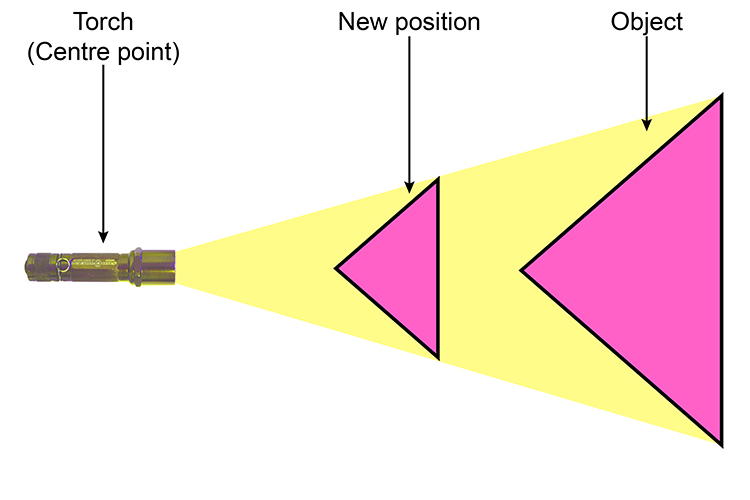
Resizing is different. Resizing will not only require a scale but will also ask for a centre point of origin.

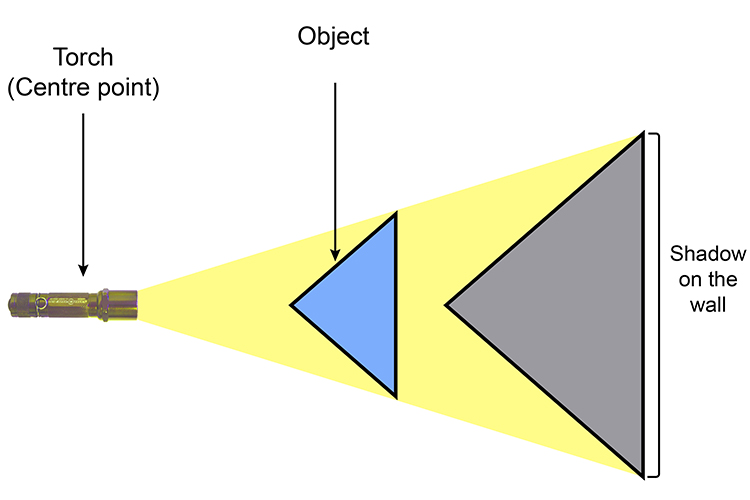
Think of resizing, enlargement or contraction as a torch shining from the centre point to the object and the resize depending on the scale.

Enlargement by a scale of 2.

The torch is the centre point and the cross-sections of the beam can be scaled at different points

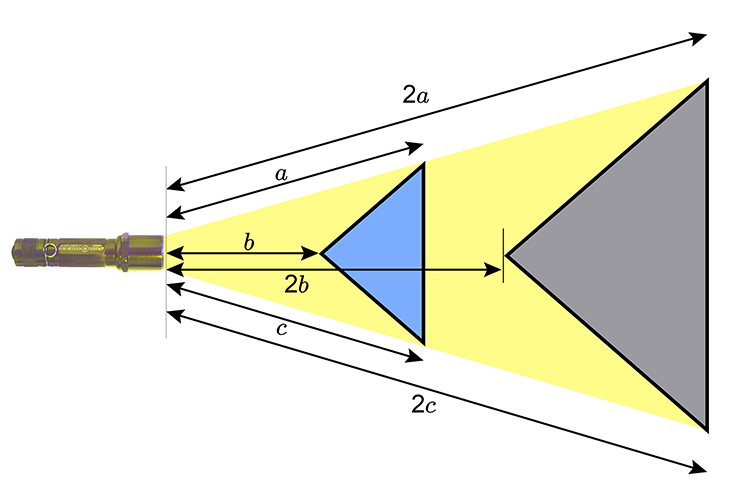
Measure each corner of the smaller triangle and scale up by 2

Our scale is 2 so we must multiply the distance between the centre point and each vertex (corner) by 2.

Reduction by a scale of `1/2`

Reduction is to make an object smaller but not changing the shape

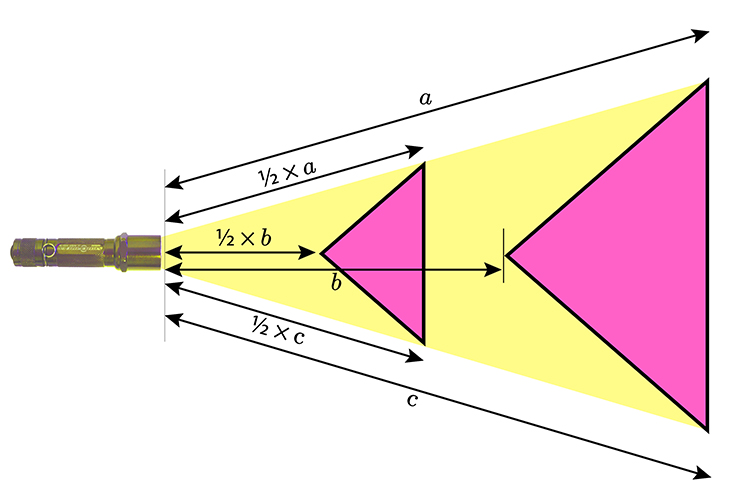
Measure the corners or the object and reduce by half

Our scale is `1/2` so we must multiply the distance between the centre point and each vertex (corner) by `1/2`.