Where can mirror lines go?

Mirror lines can go anywhere.

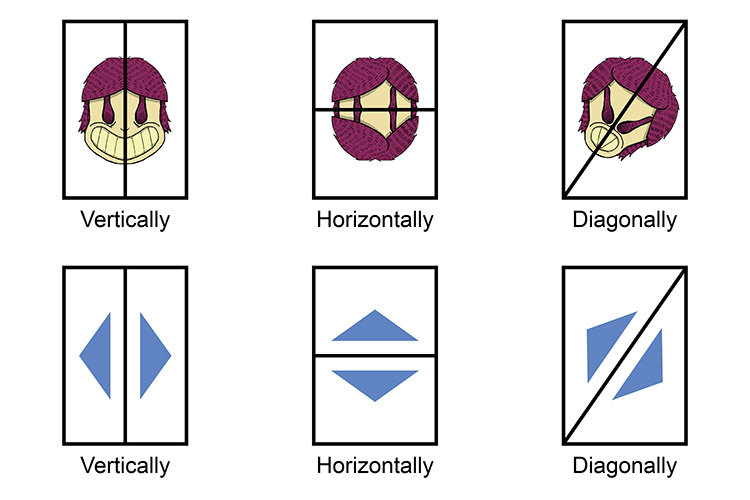
Where are the mirror lines?

Remember the formula for a straight line is:

`y=mx+c`

(you must see and learn the section on straight lines before you proceed.)

Verticle lines

Example

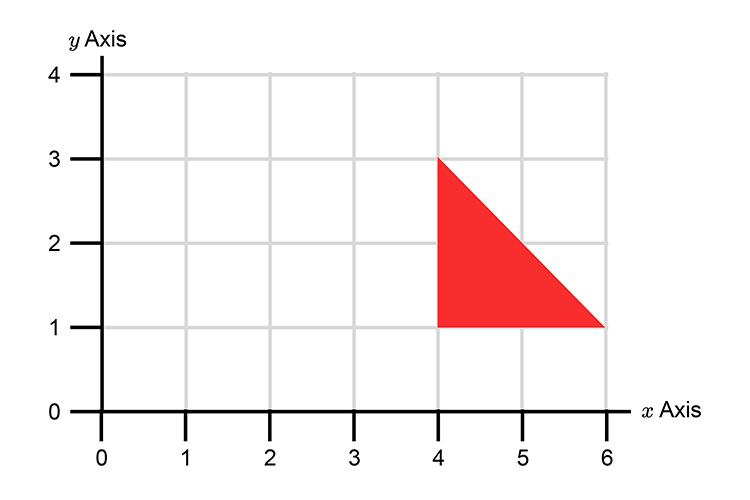
Draw a reflection of the following image with a mirror line on `x=3`.

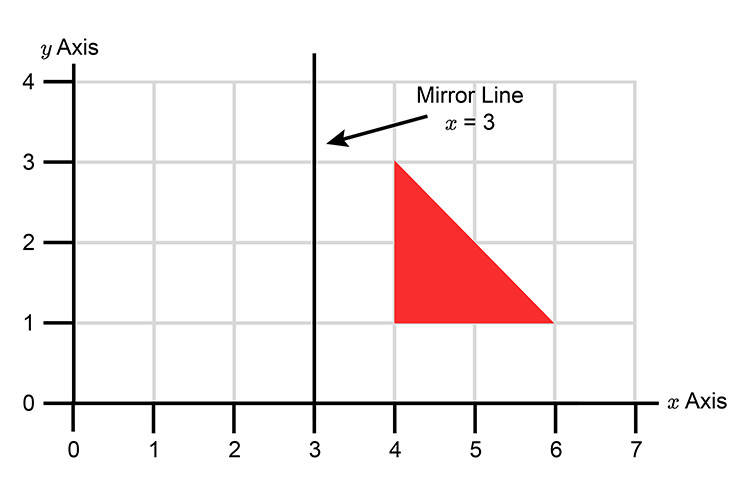
NOTE:

For `x=3`  we can work out that if:

`y=1`  then `x=3`

`y=2`  then `x=3`

`y=3`  then `x=3`  etc

If we plot this on our graph we can find the mirror line.

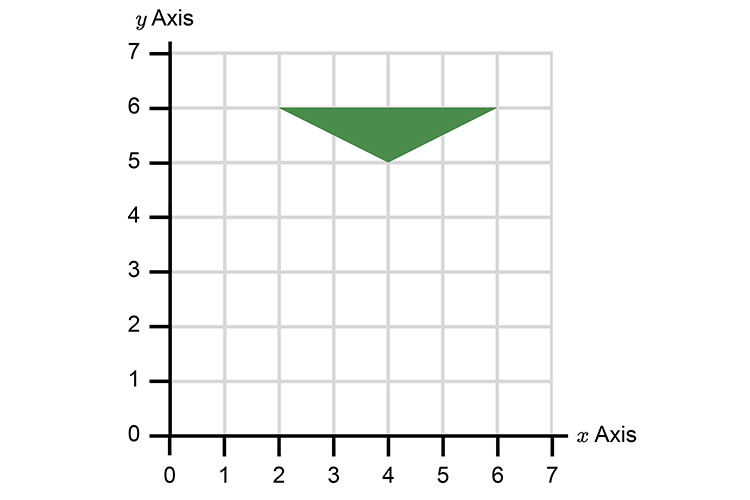
We can now complete the reflection.

Horizontal lines

Example

Draw a reflection of the following image with a mirror line on `y=4`.

NOTE:

For `y=4`  we can work out that if:

`x=5`  then `y=4`

`x=4`  then `y=4`

`x=3`  then `y=4`  etc

If we plot this on our graph we can find the mirror line.

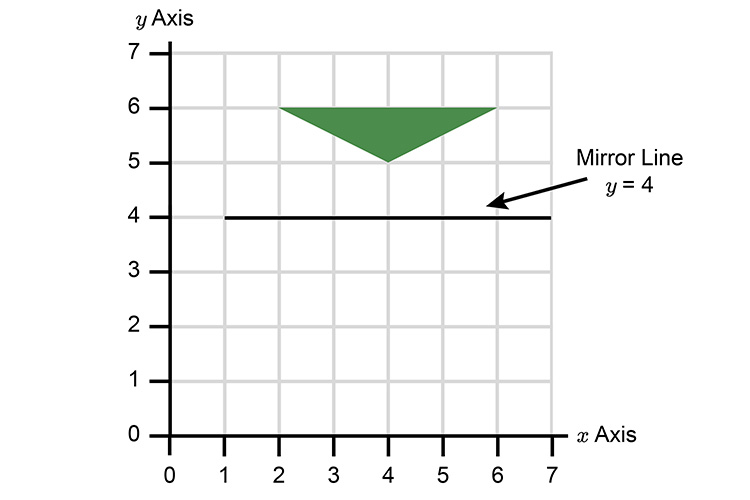
We can now complete the reflection.

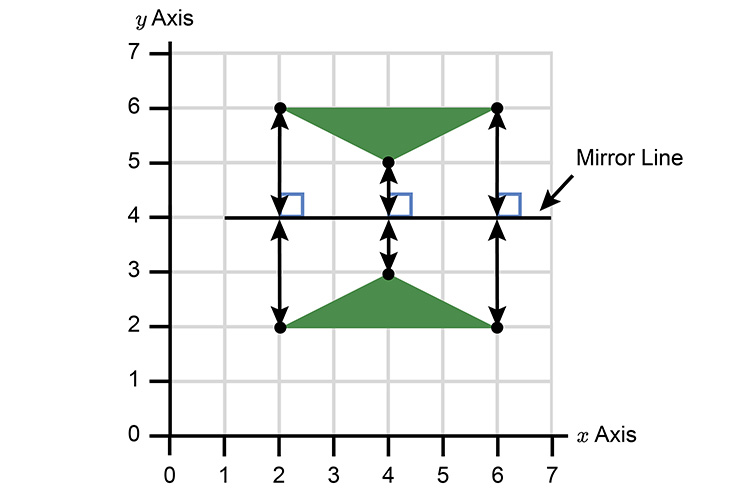
Diagonal lines

Example 1

Draw a reflection of the following image with a mirror line on `y=x`.

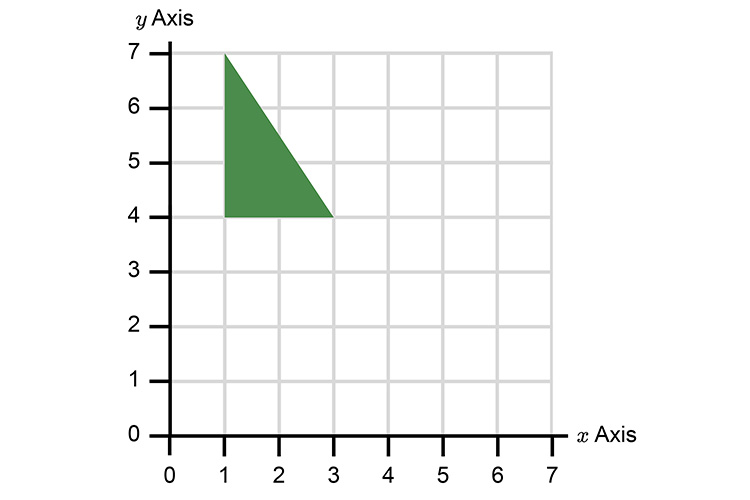
NOTE:

For `y=x`  we can work out that if:

`y=1`  then `x=1`

`y=2`  then `x=2`

`y=3`  then `x=3`  etc

If we plot this on our graph we can find the mirror line.

We can now complete the reflection.

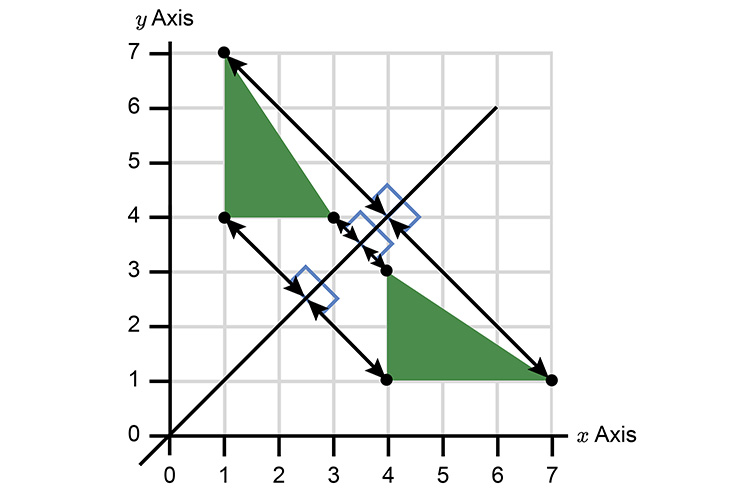
Example 2

Draw a reflection of the following image with a mirror line `y=-x`.

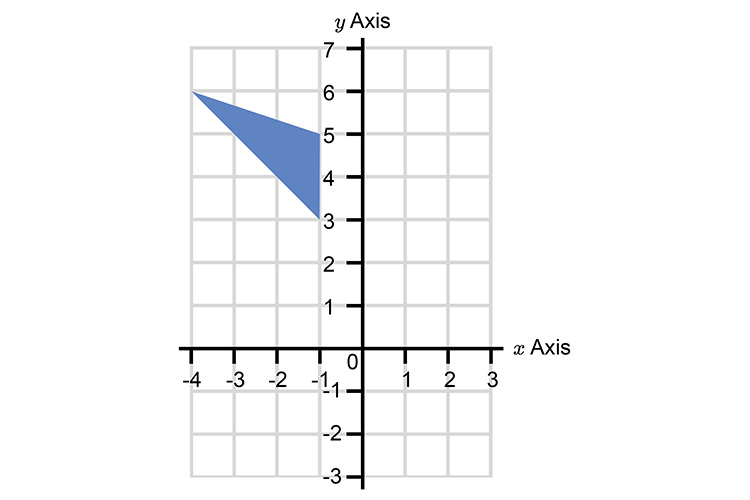
NOTE:

For `y=-x`  we can work out that if:

`y=1`  then `x=-1`         `(1=-1timesx`    therefore   `x=-1)`

`y=2`  then `x=-2`

`y=3`  then `x=-3`  etc

If we plot this on our graph we can find the mirror line.

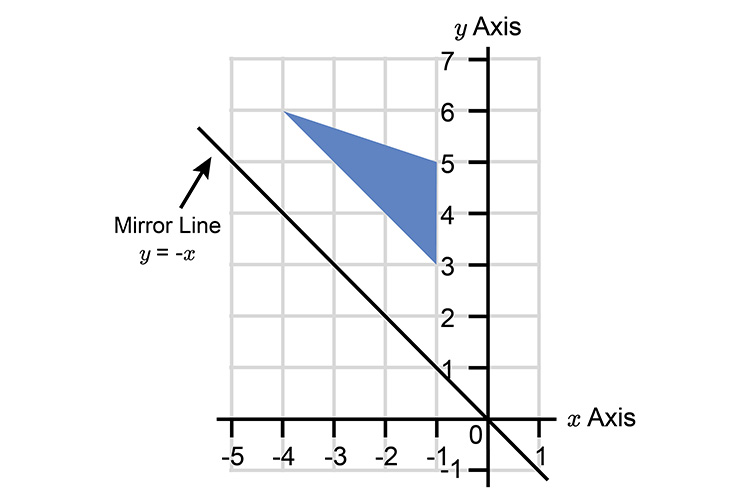
We can now complete the reflection.

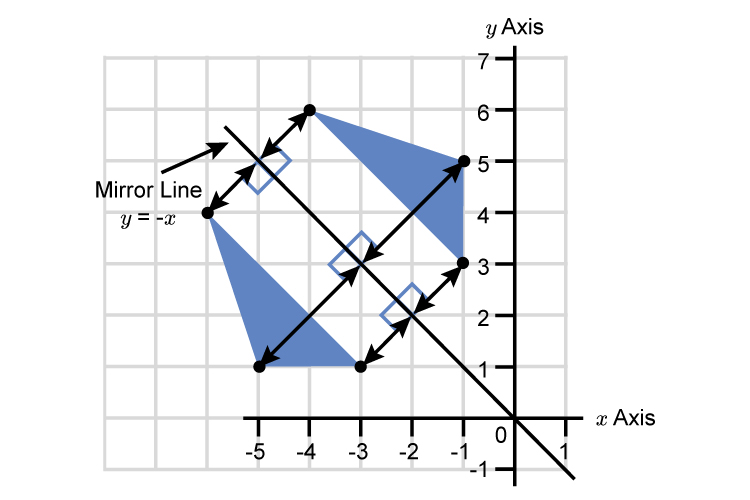
Other examples

Example 1

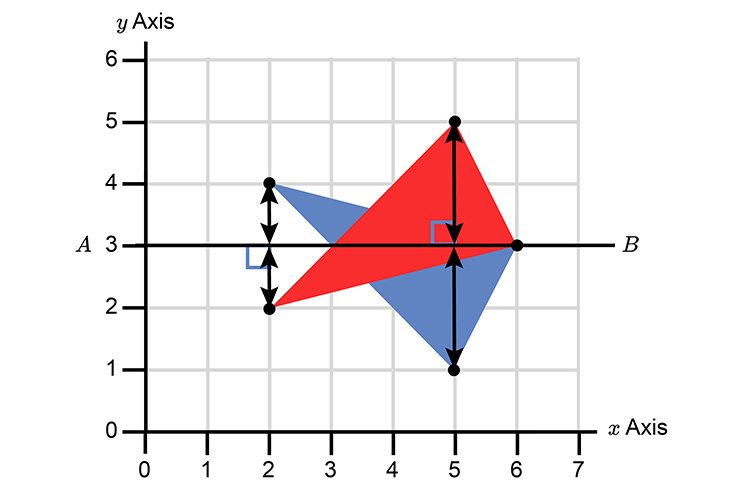
On the grid below reflect the triangle in the line A, B.

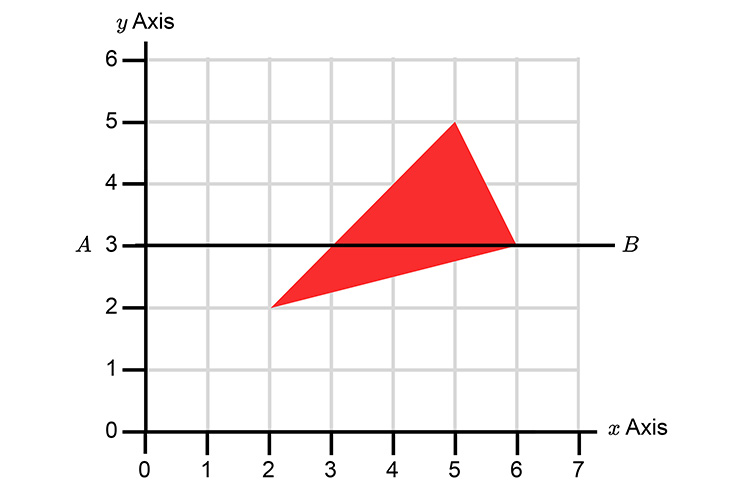
Redraw as follows:

Example 2

Describe the single transformation that maps A to B.

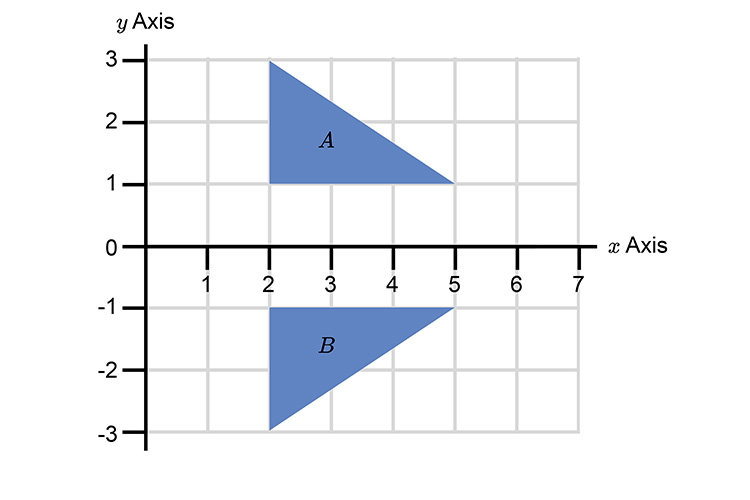
You must first describe what this is and it is a REFLECTION.

You must now find the mirror line.

This is easy because we can describe this as a mirror line along the `x` axis.

Or

If you want to get technical, it is the line `y=0`.

i.e. `x=1`  then `y=0`         

      `x=2`  then `y=0`

      `x=3`  then `y=0`  etc

Answer:

This is a reflection where the mirror line is on the `x` axis.