Frustums

A frustum is the shape you are left with if you cut the top part (the pointy bit) of a cone or pyramid off parallel to its base.

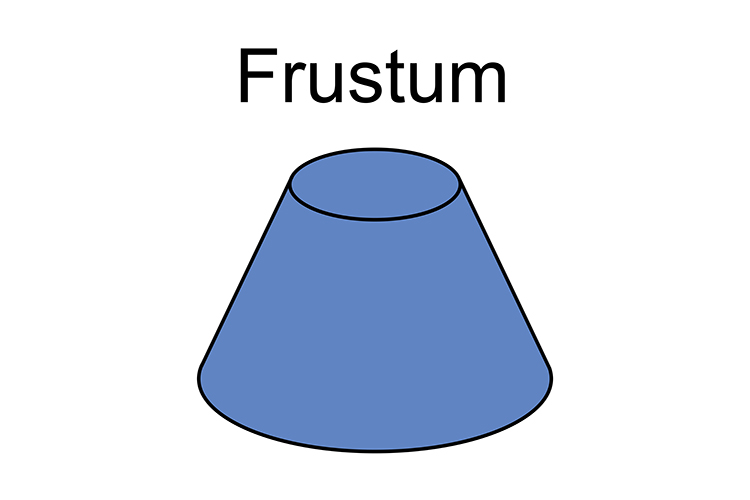
To remember this picture the following:

Wow was she frustrated (frustum) she lost the whole of the top of her ice cream cone. (The frustum is the bit that fell on the floor).

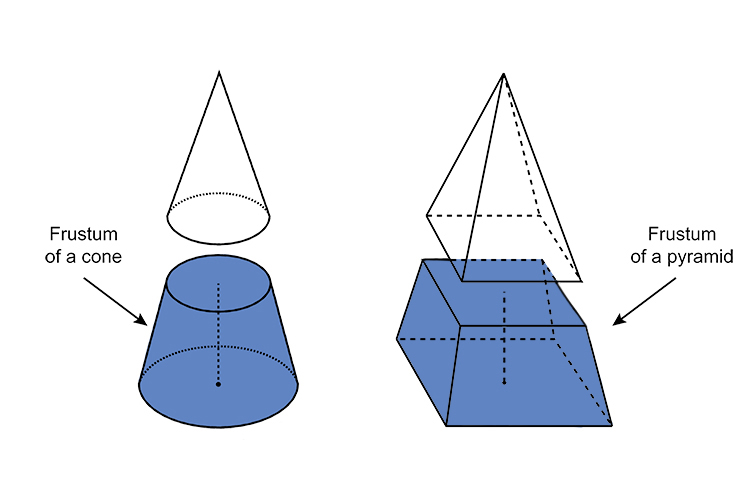
Example

The first diagram shows a cone of base radius 12 cm and perpendicular height 10 cm. A small cone of base radius 6 cm and perpendicular height 5 cm is cut off the bottom to leave a frustum. The frustum has a lower radius of 6 cm, an upper radius of 12 cm and a perpendicular height of 5 cm (see second diagram).

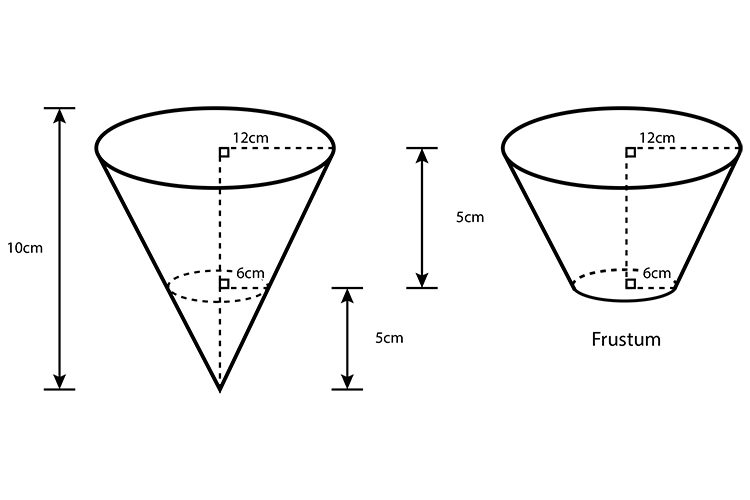
Find the volume of the frustum, giving your answer in terms of `pi`.

Answer:

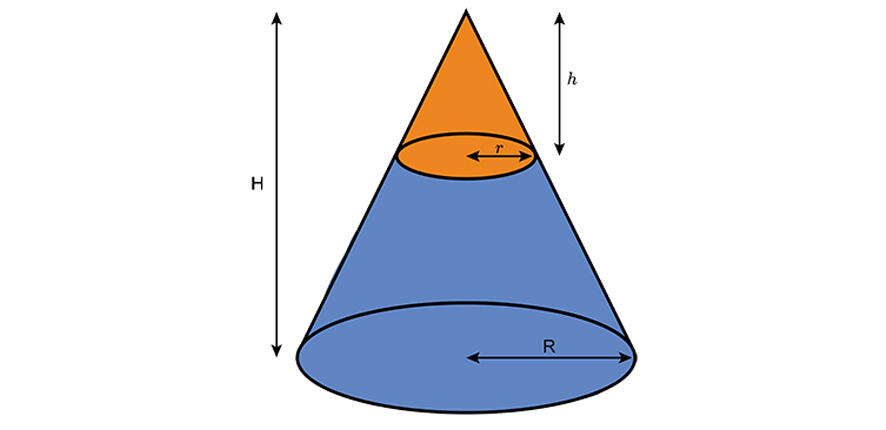
`Volume\ of\f\rustum=1/3piR^2H-1/3pir^2h`

`Volume\ of\f\rustum=(1/3pi12^2\times10)-(1/3pi6^2\times5)`

`Volume\ of\f\rustum=(1/3pi144\times10)-(1/3pi36\times5)`

`Volume\ of\f\rustum=(1/3pi\times1440)-(1/3pi\times180)`

`Volume\ of\f\rustum=(480pi)-(60pi)`

`Volume\ of\f\rustum=420pi`

Answer: 

`420picm^3`