Surface area cylinder

The surface area of any shape can be found by adding together the surface areas of its parts.

Cylinder

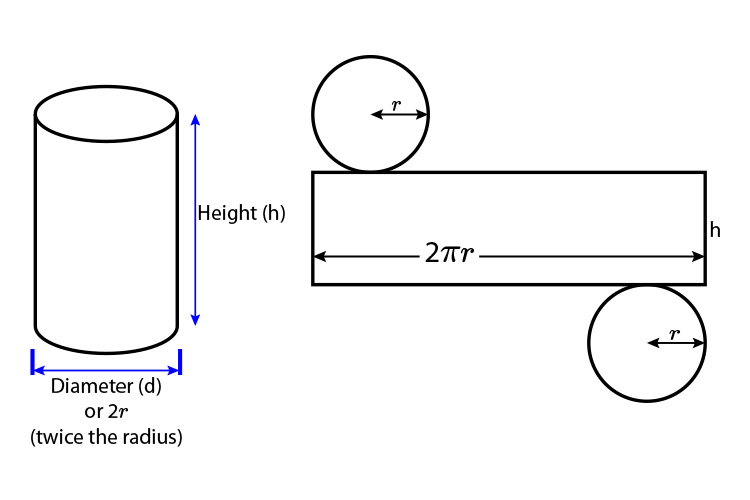
Taking apart a cylinder by adding 2 circles and a rectangle

If you always imagine pulling apart the cylinder and drawing it out you can clearly see that the areas are one rectangle and two areas of a circle (the top and bottom).

The rectangle

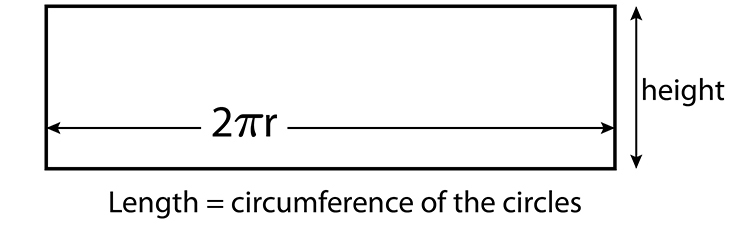
To find the area of the rectangle its height multiplied by length

The area of the rectangle is Height = $h$ multiplied by Length = $2\pir$

Area of rectangle = $h\times\2\pir$

The circle areas are:

First find the radius then its pie r squared as there are 2 circles is 2 pie r squared

Area = $\pir^2$

And because there are two circles

Area = $2\pir^2$

Summary

Area of a cylinder:

$h2\pir + 2\pir^2$

Example 1

Ted has a cylinder of height 15 cm and diameter 8 cm. He calculates the curved surface area as
$2×\pi\times8×15$ . Explain what he has done wrong.

Answer:

He used the diameter not the radius (Circumference = $2\pir$ )

Or

He incorrectly multiplied by 2 when calculating the circumference (Circumference = $\pid$ ).