Volume of a sphere

The volume of a sphere is `4/3\pir^3`

You may look at this and ask how am I going to remember this formula but actually, it’s quite easy to work out, it takes seconds: Just remember: Two cones = sphere:

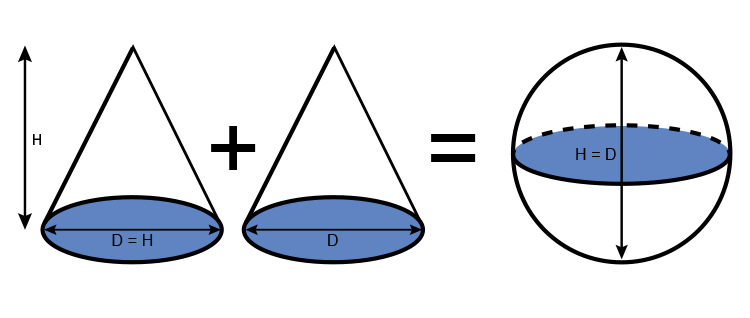
A sphere is the same as 2 cone volumes

NOTE:

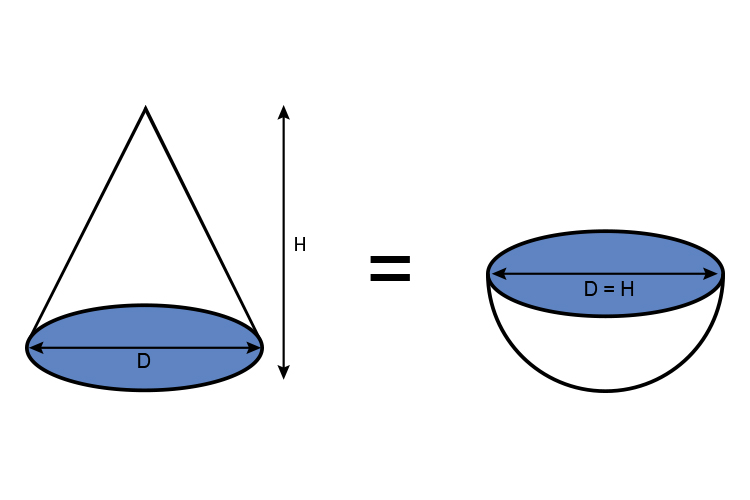
The areas shaded are all the same size (that is D=H).

We know that volume of a cone is

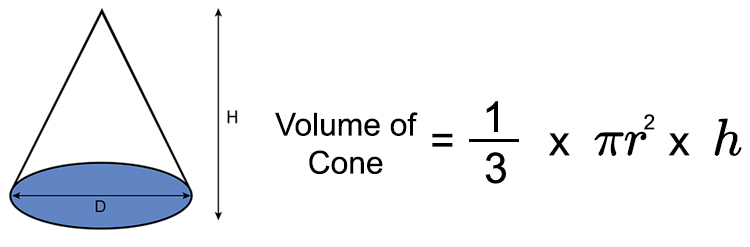
To measure a cone you need to multiply base and height then multiply another factor

Volume of cone = `1/3\timesπr^2\timesh`

Therefore volume of a sphere:

`(1/3\times\pir^2\timesh)+(1/3\times\pir^2\timesh)=` Volume of a sphere

As `h = 2r` then

`(1/3\times\pir^2\times2r)+(1/3\times\pir^2\times2r)=` Volume of a sphere

And that’s the same as:

`(2/3\times\pir^3)+(2/3\times\pir^3)=` Volume of a sphere

Which again is the same as:

`2(2/3\times\pir^3)=` Volume of a sphere

`(2\times2)/3\timespir^3=` Volume of a sphere

And

`4/3\timespir^3` = Volume of a sphere

NOTE:

The volume of one cone must be the same volume as a hemisphere (if they have the same radius and the height of the cone is the diameter of the sphere).

Hemisphere = `1/2` a sphere

2 cone is equal to a half sphere's volume