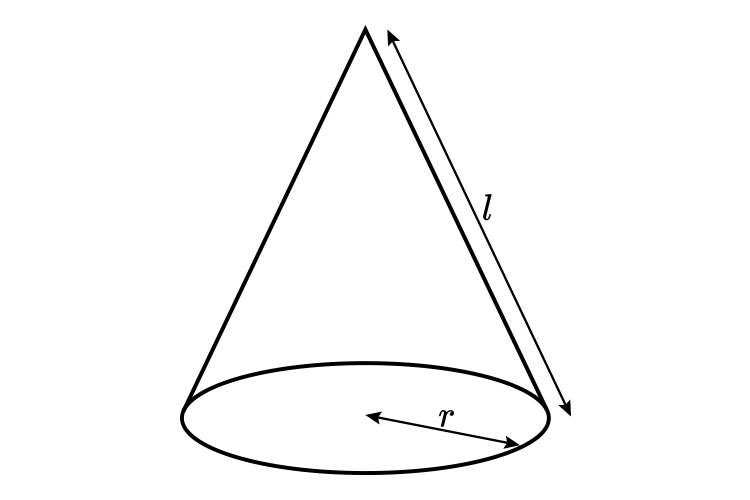
Surface area of a cone

The formula for the surface area of a cone is:

`pir^2+pirl`

Where

This formula is easier to remember if you imagine pulling apart a cone to get

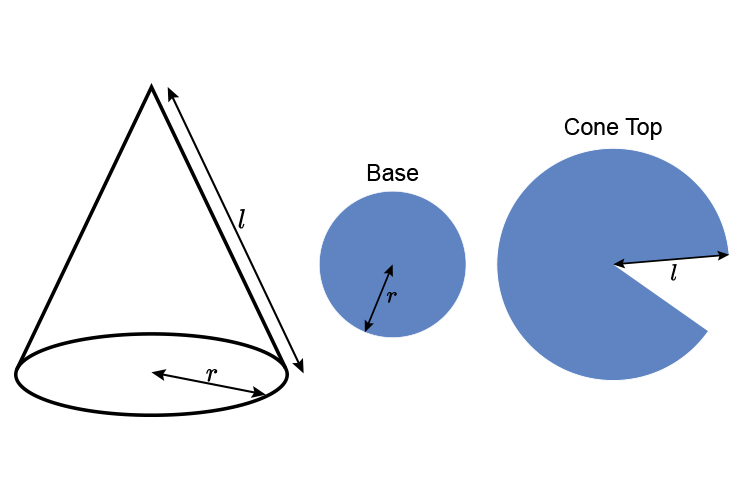
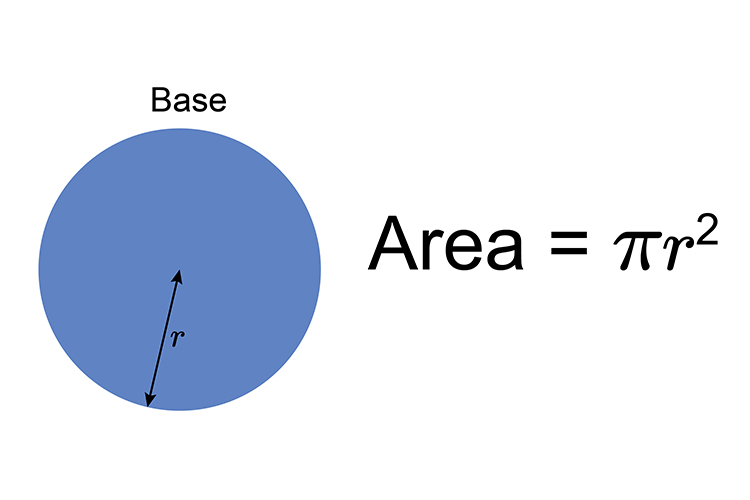
The area of the base is:

The area of the cone top is:

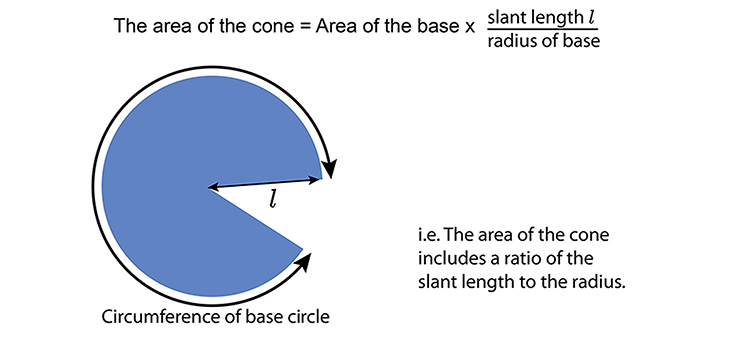
The area of the cone top = Area base x ratio slant to radius

The area of the cone top =  `\pir^2\timesratiol/r`

The area of the cone top =   `\pir^2\timesl/r`

This goes to:

The area of the cone top =  `\pirl`

Summary

Area of a cone = Area of base + Area of cone top

                           =  `\pir^2+\pirl`

Interesting example  

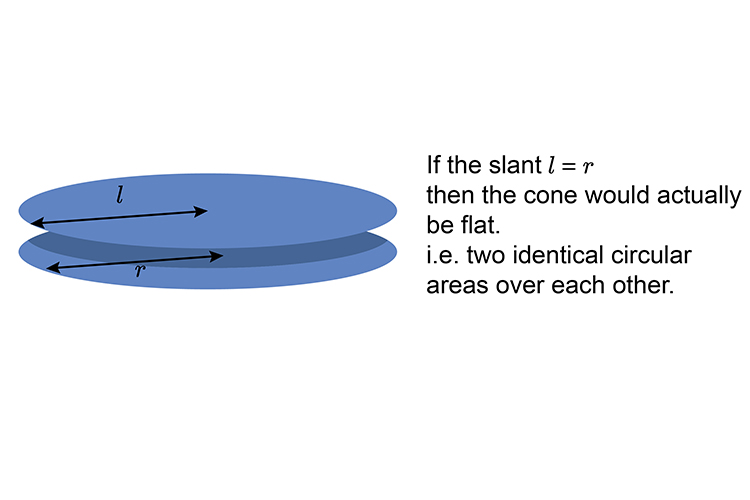
And then pulling the cone apart the surface areas would look like this:

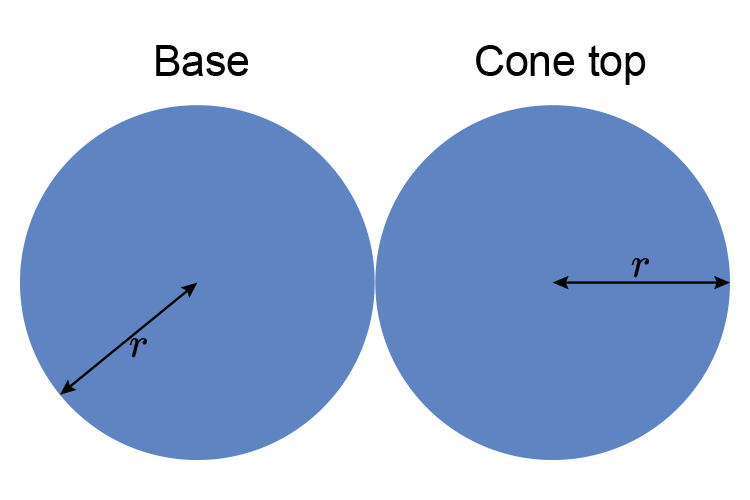
That is two full areas of circles.

Or

`\pir^2+\pir^2`

Which becomes:  `2\pir^2`

So the surface area of a cone where the slant is the same as the radius is equal to the area of two base circles `2\pir^2`

But this would never be a cone and therefore doesn’t exist under the heading “cones”.

So the way to remember the surface area of a cone is to think:

`\pir^2+\pir^2`

Only when the slant is equal to r

When it isn’t (which it can’t be as a cone).

Then the surface area of a cone must be:

`\pir^2+\pirl`