Volume examples
Example 1
A thin-walled glass paperweight consists of a hollow cylinder with a hollow cone on top as shown.
The paperweight contains just enough sand to fill the cylinder.
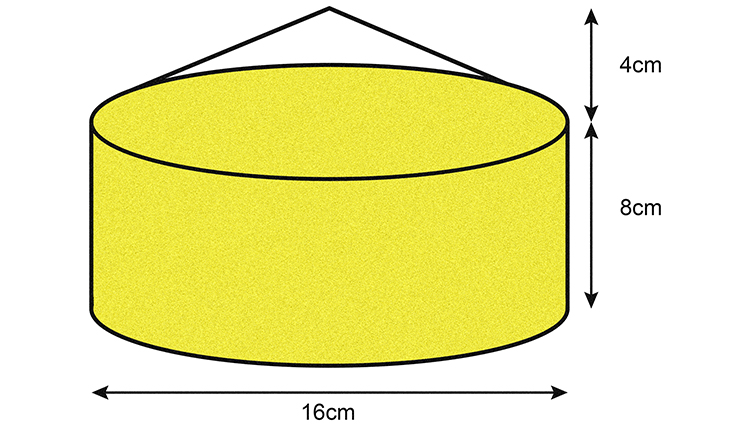
The paperweight is now turned upside down.
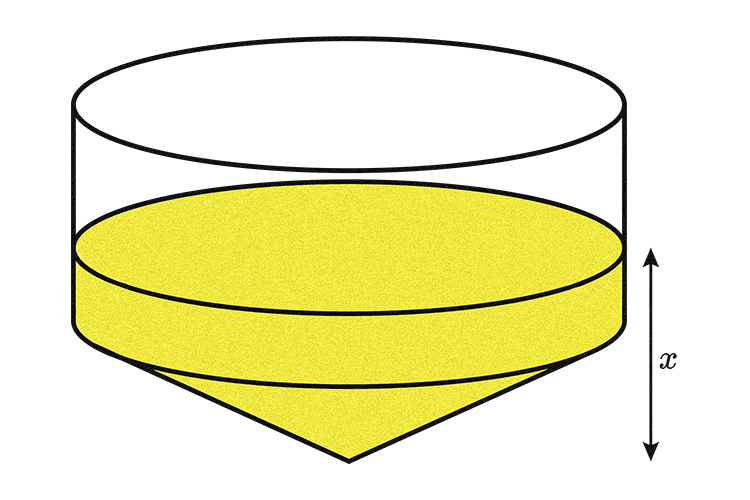
Calculate the depth of the sand (marked x in the diagram).
Answer:
Stage 1
First work out the volume of the cylinder filled by the sand before it is turned upside down.
`Volume\ of\ a\ cyl\i\nder = area\ of\ base\times height`
`Volume\ of\ a\ cyl\i\nder =\pir^2h`
The radius of the cylinder is half its diameter
Therefore the radius = `1/2\times 16 = 8cm`
Volume of the cylinder = `\pi8^2\times8=64\pi\times8=201.06\times8=1608.5cm^3`
Stage 2
Now work out the volume of the cone part of the paper weight
Volume of cone = `1/3\times\area\ of\ base\times height`
Volume of cone = `1/3\times\pir^2\ timesheight`
Volume of cone = `1/3\times\pi\times8^2\times 4 = 1/3\times 64pi \times 4 = 85.33\times\pi = 268.08cm^3`
Stage 3
Subtract the volume of the cone from the original cylinder volume
Therefore `1608.5\ – 268.08 = 1340.42cm^3`
Stage 4
Calculate the height of the sand above the cone once it has been turned upside down
The sand above the cone now forms another cylinder. We know the volume of this cylinder must equal `1340.42cm^3` therefore if we work backwards we can calculate the height of the cylinder.
Volume of a cylinder = `pir^2h`
`1340.42cm^3=pir^2h`
`1340.42=pi8^2h`
`1340.42=pi64h`
Therefore
`h=1340.42/(64pi)=1340.42/201.06=6.67cm`
Stage 5
Add the height of the cone and height of cylinder occupied by sand once the paperweight is turned upside down
Height of cone = `4cm`
Height of cylinder occupied by sand = `6.67cm`
`4 + 6.67 = 10.67cm`
Answer:
`x = 10.67cm`
Example 2
A solid cube has a square hole cut through horizontally and a circular hole cut through vertically. Both holes are cut centrally in the appropriate faces. The dimensions of the cube and the hole are shown in the diagram.
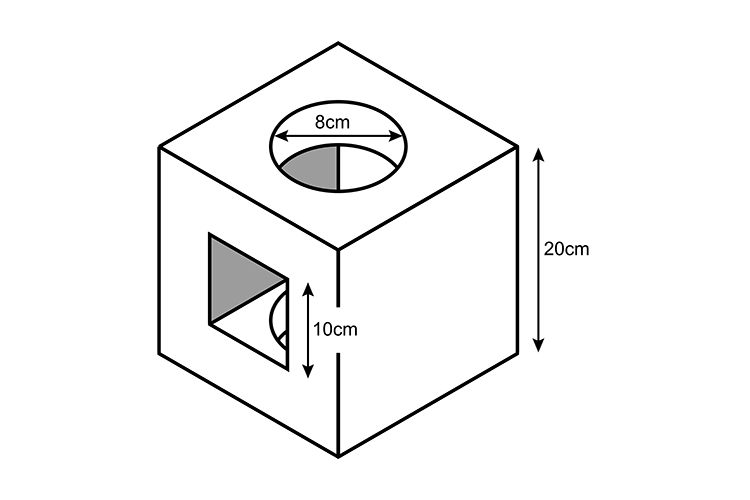
Calculate the volume remaining after the holes have been cut.
Answer:
Stage 1
First calculate the volume of the cube before the holes are cut in it.
Volume of a cube = `Area\ of\ base\times height = Leng\th\ times width\times height`
Volume of cube = `20\times 20\times 20 = 8000cm^3`
Stage 2
Work out the volume of the square hole cut into the cube.
Volume of a cuboid = `Area\ of\ base\timesheight = Leng\th\times width\ times height`
Volume of a cuboid = `20\times 10\times 10 = 2000cm^3`
Stage 3
As the square hole occupies most of the space formed from the cylindrical hole, the cylindrical hole can be treated as two smaller cylinders at the top and base of the main cube. The volume of these smaller cylinders are:
Volume of one cylinder = `area\ of\ base\times height`
Volume of one cylinder = `πr^2\timesh`
Radius of a cylinder = `1/2` diameter = `8/2=4cm`
Height = `(20-10)/2=10/2=5cm`
Volume of one cylinder = `pi4^2times5`
Volume of one cylinder = `50.27\times5 = 251.35cm^3`
Volume of two cylinders = `251.35\times2 = 502.7cm^3`
Stage 4
Subtract volume of square hole and two small cylinders from the original cube volume.
Original cube volume = `8000cm^2`
Volume of cuboid hole = `2000cm^3`
Total volume of the two small cylindrical holes = `502.7cm^3`
Therefore the remaining volume after the holes are cut is = `8000\ –\ 2000\ – 502.7`
`8000\ –\ 2502.7 = 5497.3cm^3`
Answer:
The remaining volume after the holes are cut is `5497.3cm^3`
Example 3
A solid sphere of radius 3 cm just fits inside a hollow cone of radius 6cm and height 8cm. A (vertical) cross-sectional view is shown in the diagram.
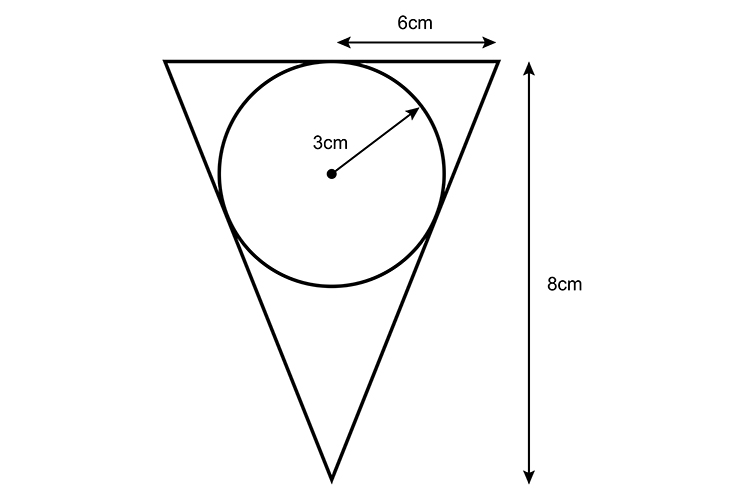
Calculate the fraction of the volume of the cone taken up by the sphere. You must show your working.
Answer:
Stage 1 – First calculate the volume of the cone.
Volume of a cone = `1/3\times\area\ of\ base\ times height`
Volume of a cone = `1/3\times pir^2\times height`
Volume of a cone = `1/3\times pi6^2 \times 8`
Volume of a cone = `1/3\times pi36\times 8 = 301.6cm^3`
Stage 2
Calculate the volume of the sphere.
Volume of a sphere = `4/3pir^3`
Volume of the sphere = `4/3pi3^3`
Volume of the sphere = `4/3pi27`
Volume of the sphere = `113.1cm^3`
Stage 3
The fraction of the cone taken by the sphere.
Volume of a cone = `301.6cm^3`
Volume of the sphere = `113.1cm^3`
`301.6cm^3=1(100%)`
`113.1cm^3 = x`
(see calculating percentages for this method)
`301.6/113.1=1/x`
`x=1\times113.1/301.6`
`x=113.1/301.6`
Example 4
A hemispherical bowl of radius 6 cm has the same volume as a cone of perpendicular height 27 cm.
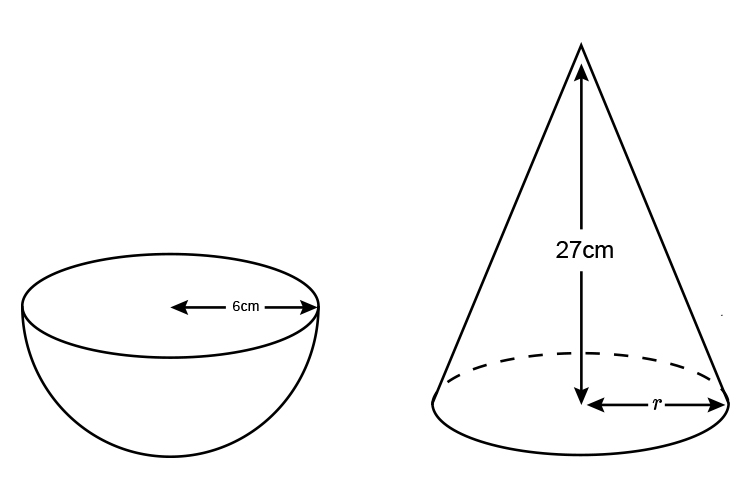
Calculate the base radius, r, of the cone (without using a calculator – you must show all working).
Answer:
Volume of a hemisphere = `1/2\ area\ of\ a\ sphere`
Volume of a sphere = `4/3pir^3`
Therefore the Volume of a hemisphere =`1/2\times4/3pir^3=4/6pir^3`
Volume of the hemisphere = Volume of the cone
Volume of cone = `1/3\timespir^2\times height`
Therefore `4/6pir^3=1/3pir^2h`
`4/6pi6^3=1/3pir^2\times27`
`4/6pi6\times 6\times6=1/3pir^2\times27`
`4/cancel6pi6\times 6\timescancel6=1/cancel3pir^2\timescancel27\9`
`4\cancelpi6times6=cancelpir^2\times 9`
`4times6\times 6=r^2\times9`
`r^2=(4\times6\times6)/9`
`r^2=4\times36/9`
`r^2=(4\timescancel36\4)/cancel9`
`r^2=4\times4`
`r^2=16`
Therefore `r=\sqrt16`
Therefore `r=4`
Answer:
`r=4cm`




